2.2.3.2. Обработка результатов измерений диагонального хода

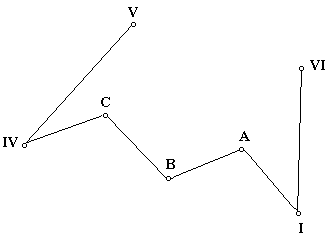
Диагональный ход в данном задании рассматривается как разомкнутый теодолитный ход (рис. 2.3).

П

Рис. 2.3. Схема диагонального хода

режде чем приступить к вычислению дирекционных углов диагонального хода, необходимо проверить и исправить углы. В разомкнутом теодолитном ходе проверка правильности измерения углов производится по величине угловой невязки, определяемой по формуле

f_βПР =Σβ_i – n180° –

– (_Н –_К), (2.13)

где β_i – справа по ходу лежащие углы диагонального хода; _Н, _К – дирекционные углы сторон полигона (начальной и конечной), к которым примыкает диагональный ход своими концами.

В примере:

f_βПР = 689° 44 30 – 5180° – (193°40 – 43°57) = +1°30.

Предельная угловая невязка определяется по той же формуле, что и для основного многоугольника.

После этого допустимую угловую невязку распределяют между углами диагонального хода (кроме примычных) так, как это было указано для замкнутого хода.

Далее, пользуясь исправленными углами, вычисляют дирекционные углы, приняв за исходное направление (VI–I), известное из замкнутого хода.

Контролем правильности вычислений служит получение дирекционного угла стороны IV–V, к которому приведут последовательные правильные вычисления всех направлений разомкнутого хода.

2.2.4. Вычисление осевых румбов

Так как при дальнейших вычислениях и графических работах удобнее иметь дело с осевыми румбами, а не с дирекционными углами, необходимо от них перейти к румбам.

Переход следует осуществлять особенно внимательно, так как контроля при этом нет.

2.2.5. Определение горизонтальных проложений сторон хода

Как известно, на планах наносятся горизонтальные проложения линий, а при вычислении приращений координат вместо измеренных наклонных расстояний используют горизонтальные проложения, поэтому необходимо от измеренных непосредственно на местности наклонных расстояний перейти к горизонтальным проложениям (проекции наклонных расстояний на горизонтальную плоскость).

Вычисляют их по формуле

S = Д  cos, (2.14)

где Д – измеренная (наклонная) длина линии;  – угол наклона линии к горизонту.

Углы наклона линий определяют по формуле

, (2.15)

где Л и П – отсчеты по вертикальному кругу теодолита на каждую из наблюдаемых вершин (берутся из журнала измерения углов и линий табл.2.1 и 2.2).

Полученные по формуле (2.14) расстояния записывают в графу «Исправленная длина линий» в табл.2.1 и 2.2 и в графу «Горизонтальное проложение линий» в табл.2.3.

2.2.6. Построение планового съемочного обоснования

Для контроля полевых измерений и вычислений плановая опорная сеть накладывается на бумаге. Как правило, накладка сети делается по румбам и длинам сторон. При этом положение первой вершины выбирается с таким расчетом, чтобы сеть разместилась на листе бумаги и была расположена в его центральной части. Через первую вершину проводится направление меридиана в виде вертикальной линии, и с помощью транспортира от него откладывается угол, равный румбу первой линии с учетом четверти, в которой располагается данная линия. От первой вершины по полученному направлению проводится прямая линия и в заданном масштабе от нее откладывается длина горизонтального проложения первой линии. Полученная таким образом точка будет второй вершиной теодолитного хода. Через нее также проводится направление, параллельное направлению меридиана, проведенного через первую вершину, транспортиром откладывается румб второй линии, на полученном направлении – длина горизонтального проложения второй линии и т.д., пока, наконец, не будет отложена длина горизонтального проложения последней линии. Многоугольник при этом, как правило, не должен замкнуться (рис. 2.4), так как полевые измерения, с одной стороны, и графические работы – с другой, содержат в себе погрешности, которые, суммируясь, дадут линейную невязку, называемую практической. В случае если полевые и графические погрешности носили случайный характер, невязка не будет превосходить 1:200 периметра многоугольника. поэтому величина, равная 1:200 периметра теодолитного хода (полигона), называется предельной линейной невязкой.

Если практическая линейная невязка будет превосходить указанный предел, необходимо, прежде всего проверить графические работы, затем вычисления, и если и это не даст ожидаемого результата, значит в полевых измерениях (вероятнее всего в измерениях сторон) имеются грубые ошибки. Для их устранения необходимы повторные измерения. Если допущена ошибка в измерении или отложении длины только одной стороны, то линейная невязка будет приблизительно параллельна этой ошибочной стороне. Следовательно, необходимо сначала проверить вычисление и отложение в масштабе длины той стороны, которая параллельна невязке, и если на чертеже ошибки нет, необходимо заново измерить длину этой стороны на местности.

В случае если ошибка допущена в определении румба или в отложении румба какой-нибудь одной стороны, необходимо проверить вычисление и отложение румба той стороны, которая будет приблизительно перпендикулярна линейной невязке.

Практическая линейная невязка, не превосходящая 1:200 периметра, называется допустимой, и в случае если план, составленный по румбам сторон хода, является окончательным, распределяется между всеми вершинами пропорционально длине сторон.

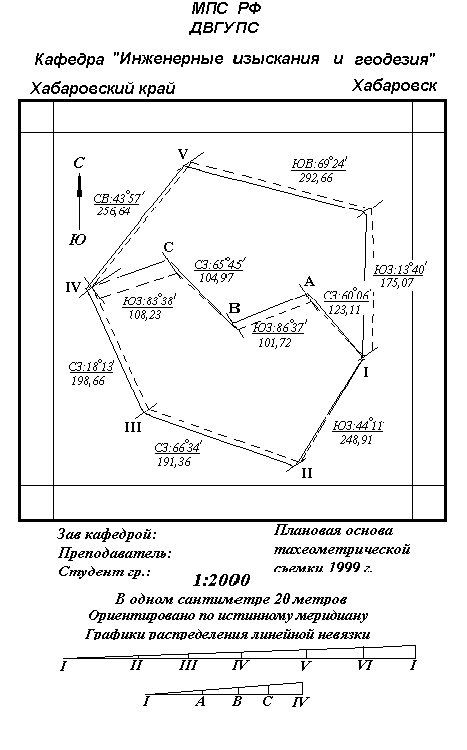
Рис. 2.4. Пример построения плановой опорной сети по румбам и длинам сторон

Для определения долей невязки пропорциональных длинам сторон, удобнее всего построить график распределения линейной невязки. Для этого на прямой линии откладывают последовательно длины всех сторон в уменьшенном масштабе по сравнению с масштабом плана. В конце этой линии по перпендикуляру откладывают полученную практическую линейную невязку безо всяких изменений. Соединив конец невязки с начальной точкой графика, получают прямоугольный треугольник.

Из точек, которые являются концами отложенных сторон, восстанавливают перпендикуляр до пересечения с гипотенузой построенного прямоугольного треугольника. Эти перпендикуляры и будут долями невязки для каждой вершины полигона.

Чтобы увязать полигон (замкнуть), необходимо через каждую его вершину провести отрезки, параллельные невязке. На этих отрезках откладывают доли невязки для каждой вершины в направлении невязки, т.е. от конца последней отложенной стороны многоугольника к исходной первой точке. Затем исходную точку соединяют с новой точкой для второй вершины, эту последнюю – с новой для третьей вершины и т.д., и наконец, вновь полученную точку для последней вершины соединяют с исходной точкой, замыкая таким образом многоугольник.

Так же строится и диагональный ход. Поскольку диагональный ход начинается от вершины I, в этой точке от направления меридиана с помощью транспортира откладывается румб стороны I–А и горизонтальное проложение линии. Несовпадение конца диагонального хода с точкой, к которой он должен примыкать, является практической линейной невязкой диагонального хода. Допустимость практической линейной невязки определяется по предельной, которая может быть определена как 1:200 периметра диагонального хода.

Увязка осуществляется аналогично описанному выше. Разница лишь в том, что линейная невязка в этом случае распределяется только на вершины диагонального хода.

Убедившись в отсутствии грубых погрешностей в полевых измерениях, по допустимости линейной невязки в накладке опорной сети по румбам приступают к вычислению приращений координат и координат пунктов опорной сети.