Баланс мощностей.
Мощность нагрузки:
Š2= I22*Z2 =(2.762)2*70 = 735.012 Вт
Ucb= I3*Z3 – I4*jXМ = -225.66 + j28.29 B
Š3= Ucb*I3*=(-225.66 +j28.29)(-0.8014 – j0.519)= 195.54 + j94.46 Вт
Uba= I4*Z4 – I3*jXМ = 148.96 – j149.63 B
Š4= Uba*I4*=(148.96 – j149.63)(-0.335 + j2.203)= 279.8 + j378.3 Вт
Š5= I52*Z5= (4.461)2*(35 – j35) = 696.4 – j696.4 Вт
Š∑нагр= Š2+ Š3+ Š4+ Š5= 1907 – j223.62 Вт
Мощность источников питания:
Še1= E1*I1* =(70 + j121.24)(-0.467 – j2.722)= 297.41 – j247.13 Вт
Še2= E2*I2*=(147.22 – j85)(3.199 – j0.519)= 426.71 – j348.3 Вт
ŠJ=Ucd*J*=(295.65 – j92.95)(-4 –j0)= 1183+j371.8 Вт
Š∑ист= Še1+ Še2+ ŠJ= 1907 – j223.62 Вт
Š∑нагр = Š∑ист
Сделаем развязки индуктивных связей в схеме, выделим из схемы ветвь ab и определим параметры активного двухполюсника.
Z5
d
Для
развязки индуктивных связей уменьшим
реактивное сопративление ветвей
индуктивно связанных катушек (XL-XM)
и добавим катушку (jXM)
в ветвь bd.
c
i5
2R
R
I1
J
I5
jXM
j(XL-XM)
j(XL-XM)
I4
Z2
E2
I2
I3
E1
a
b
Z5
d
c
2R
a
b
jXM
j(XL-XM)
Находим
Zген
Z2
Z3’
Zген=Zabxx=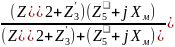
= 30.1 + j0.7 Ом
Oпределим параметры активного двухполюсника.
Z5
d
Находим
Ubaxx,
для этого рассчитываем схему методом
контурных токов. Считаем,
что I11X=J=
=-4 + j0 A.
c
i5
2R
I1X
Ucdxx
I11X
I5X
J
I22X
jXM
j(XL-XM)
Z2
E2
E1
a
b
Z3’
I3X
I2X
Ubaxx
I11X(Z3’
+ jXM)
+ I22X(Z3’
+ jXM)
= E1
+ Ucdxx
I11X(Z3’ + jXM) + I22X(Z3’ + jXM + Z5 + Z2)= E1 + E2 (2)
Из
(2) I22X=
= 3.29 + j0.821 A
I2X= I22X= 3.29 + j0.821 A
I3X= I11X + I22X= -0.71 + j0.821 A
Ubaxx + I2X*Z2 + I3X*Z3’=E2
Eген=Ubaxx=E2 - I2X*Z2 - I3X*Z3’= 45.133 – j232.51 B
Eген
Zген
I4=
= -0.335 – j2.203 A
j(XL-XM)
Z4
I4
R
Изменяя сопротивление ветви ab от 0 до 10*Zген, рассчитываем и построим зависимость Pab = f(Rab).
Rab
Rab |
Pab |
0 |
0 |
30,106 |
344,73 |
60,216 |
358,162 |
90,324 |
321,175 |
120,433 |
282,271 |
150,541 |
249,075 |
180,649 |
221,802 |
210,757 |
199,422 |
240,865 |
180,893 |
270,973 |
165,374 |
301,081 |
152,224 |
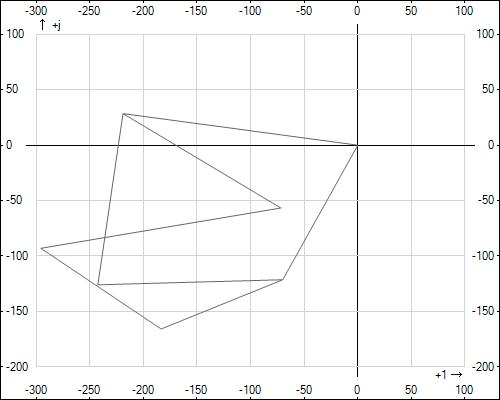
Лучевая диаграмма и совмещенная с ней топографическая диаграмма напряжений.
φd= 0 +j0 B φa= φd+I5*Z5=-218,96 + j28,39 B φm= φa +E2=-71,76 – j56,61 B φc= φm –I2*Z2=-295,66 – j92,95 B φk= φc – I3*2R = -183,45 – j165,62 B φb= φk - I3*jXL + I4*jXM = -70 – j121,24 B φd= φb +E1= 0 + j0 φn= φa – I4*R = -242,401 – j125,85 B φb= φn + I3*jXM - I4*jXL = -70 – j121,24 B φd= φb +E1= 0 + j0
|
