Содержание

2

5

6

11

18

19

Задание

Введение

Линейные цепи постоянного тока 4

Линейные цепи синусоидального тока

Заключение

Список литературы

Задание

Задание Расчет сложных электрических цепей с постоянными и гармоническими напряжениями и токами по теоретическим основам электротехники

Задача № 1

Для заданной схемы с постоянными во времени ЭДС и тока, принимая

(t)=E; (t)= ; j(t)=j.

Выполнить следующие:

1. Изобразить схему, достаточную для расчета токов во всех ветвях схемы и напряжение на источниках тока, используя два разных способа;

2. Рассчитать баланс вырабатываемой и потребляемой мощности;

3. Представить цепь относительно ветви ab активным двухполюсником, определить его параметры, построить внешнюю характеристику двухполюсника и по ней графически определить ток ветви 01 в;

4. Для любого контура без источника тока рассчитать и построить потенциальную диаграмму;

5. Определить показания вольтметра.

Задача № 2 Для заданной схемы, с источником гармонических сигналов, принимая =314 рад/сек, М=L/2

(t)= sin( t + )

(t)= sin( t + )

J(t)= Jsin( t + )

Выполнить следующее:

1. Рассчитать комплексные сопротивления ветвей, соединяющих узлы, помеченные на схемах буквами и изобразить комплексную схему замещения с этими сопротивлениями для расчета комплексов действующих значений токов ветвей (номера и направления токов сохранить согласно п.1 задачи 1, причем параллельное соединение R и C представить в виде одного комплексного сопротивления);

2. Не исключая индуктивной связи, определить комплексы действующих значений токов всех ветвей и напряжение на источнике тока. Записать мгновенное значение тока ветви и ЭДС (t) и напряжение на источниках тока;

3. Рассчитать баланс мощности активной и реактивной мощности;

4. Построить лучевую диаграмму токов и совмещенную с ней топографическую диаграмму напряжения;

5. Определить показания вольтметра;

6. Сделать развязку индуктивной связи и относительно сопротивления R ветви ab определить комплексное сопротивление активного двухполюсника (эквивалентного генератора) Zr= * ЭДС генератора Er и ток Iab ветви ab, а затем при изменении сопротивления R ветви ab от 0 до 10*Z_г рассчитать и построить зависимость активной мощности Pab=f(R)

Проанализировать использованные методы расчета, результаты вычислений и сформировать выводы по работе.

Схема задания

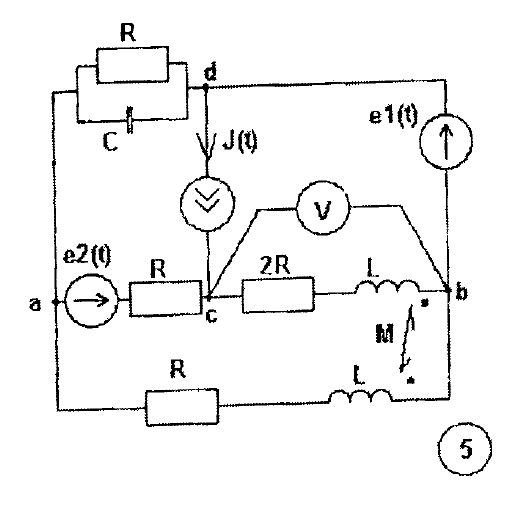
Введение

Цель данной работы состоит в ознокомлении с методами расчетов сложных электрических цепей с постоянными и гармоническими напряжениями и токами по теоретическим основам электротехники.

Линейные цепи постоянного тока

R

d

I₁

J=I₆

U_cd

Дано:

E₁=140 B

E₂=170 B

J=4 A

R=70 Oм

I₅

III

I

E₁

R

2R

E₂

I₃

I₂

а

b

c

II

R

I₄

Рассчитываем данную схему методом законов Кирхгофа:

Считаем, что нам известен один из токов(по условию I₆=J=4 A), неизвестным будем считать напряжение на зажимах источника тока(U_cd).

Составим систему уравнений по законам Кирхгофа.

По первому закону:

Для узла а: I₄ - I₂ - I₅ = 0

Для узла b: I₃ - I₁ - I₄ = 0

Для узла с: J + I₂ - I₃ = 0

По второму закону:

Для контура (dcbd): I₃*2R - U_cd = E₁

Для контура (acba): I₂*R + I₃*2R + I₄R = E₂

Для контура (dbad): I₅*R + I₄*R = -E₁

Cистема шести уравнений в матричной форме вида [A]*[X]=[B]:

0	-1	0	1	-1	0		I1		0
-1	0	1	-1	0	0		I2		0
0	1	-1	0	0	0	x	I3	=	-J
0	0	2R	0	0	-1		I4		E1
0	R	2R	R	0	0		I5		E2
0	0	0	R	R	0		Ucd		-E2

X:=(А)^-1 * В

		0	-1	0	1	-1	0				0				4.3469
		-1	0	1	-1	0	0				0				-1.3061
A	=	0	1	-1	0	0	0		B	=	-4		X	=	2.6939
		0	0	140	0	0	-1				140				-1.6531
		0	70	140	70	0	0				170				-0.3469
		0	0	0	70	70	0				-140				237.1429

I₁ = 4.347 A I₂ = -1.306 A I₃ = 2.694 A

I₄ = -1.653 A I₅ = -0.347 A U_cd= 237.14 B

Расчет методом контурных токов:

Считаем, что в цепи протекают три контурных тока I₁₁, I₂₂, I₃₃. Один из контурных токов нам известен(I₁₁=J=4 A), неизвестными будут- I₂₂, I₃₃, U_cd.

Составим систему уравнений по методу контурных токов:

I контур(dcbd): I₁₁*2R + I₂₂*2R – U_cd = E₁

II контур(acba): I_11*2R + I₂₂*4R + I₃₃*2R = E₂

III контур(dbad): I₂₂*R + I₃₃*2R = -E₁

В матричной форме виде [A]*[X]=[B] получим:

-1	2R	0		Ucd		E1 - J*2R
0	4R	R	x	I22	=	E2 - J*2R
0	R	2R		I33		-E1

X:=(A)^-1*B

	-1	140	0			-420			237.143
A=	0	280	70		B=	-390		X=	-1.306
	0	70	140			-140			-0.347

I₂₂= -1.306 A I₃₃= -0.347 A U_cd= 237.14 B

По найденным контурным токам находим токи в ветвях:

I₁ = I₁₁ – I₃₃ = 4.347 A I₄ = I₃₃ + I₂₂ = -1.653 A

I₂ = I₂₂ = -1.306 A I₅ = I₃₃ = -0.347 A

I₃ = I₁₁ + I₂₂ = 2.694 A I₆ = J = 4 A

Искомые величины в данном методе совпали с величинами, полученными методом законов Кирхгофа.