VII. Схема кранкa –ніколсона

7.1. Зауваження про стійкість і точність розв’язку

Той факт, що неявна схема (5.26) безумовно стійка, не означає, що буде отримане гарне наближене рішення при довільному співвідношенні h і . Наближене рішення схеми (5.26) має перший порядок точності за часом і другий порядок за просторовою координатою, тобто похибку апроксимації можна представити у вигляді .

Припустимо, що . Відомий обчислювальний принцип: похибки повинні бути одного порядку малості при внеску в повну похибку. Тоді для сумірності внесків у повну похибку від дискретизації за часом і дискретизацією за простором необхідно зменшити , тобто зажадати, щоб .Останнє співвідношення нагадує умову стійкості (2.22) для явної схеми.

Таким чином, хоча умова стійкості неявної схеми не накладає ніяких обмежень на співвідношення і , вимоги до точності можуть привести до виникнення подібних обмежень. Наприклад, при абсолютній точності варто вибрати h =0,1, 0,01. Найбільш прийнятна для розглянутої задачі є схема Кранка-Ніколсона.

7. 2. Побудова і рішення різницевої схеми Кранка - Ніколсона

Розглянемо ще один спосіб побудови різницевої схеми, еквівалентної (2.12)—(2.14). Згадаємо, що, згідно з (1.10), у точці (i,k)

.

Аналогічно в точці

.

Усереднюючи ці два наближення, одержимо

.

Якщо тепер для обчислення скористатися правими різницями , то кінцево-різницеве рівняння, еквівалентне (2.12), запишеться у вигляді

Якщо тепер покласти , (7.28)

то останню рівність можна представити у вигляді:

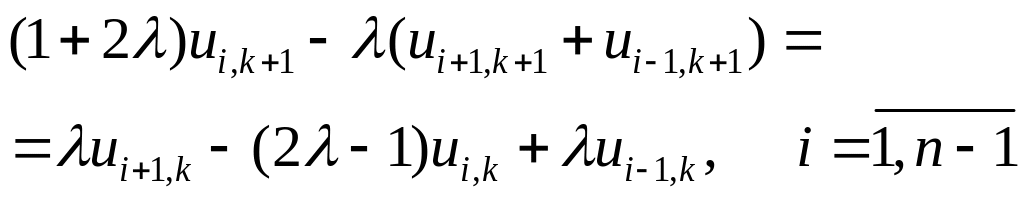(7.29)

Цей спосіб побудови кінцево-різницевого рівняння називають методом Кранка-Ніколсона. Шаблон для різницевої с х е м и Кранка-Ніколсона (7,29) представлений на рис.3.

Рис.3

Різницева схема Кранка-Ніколсона є іншим неявним методом і для обчислення значень сіткової функції , що на кожному часовому шарі вимагає рішення тридіагональної системи з (n - 1) рівнянь. Лінійну систему (7.29) можна представити в матрично-векторній формі у вигляді:

(7.30)

Отже, наближене рішення задачі (2.12) – (2.14) зводиться до рішення тридіагональної системи рівнянь (7.30) на кожному кроці за часом. Матриця коефіцієнтів цієї лінійної системи збігається з матрицею системи (5.26), а вектор правих частин (вільних членів) визначається трохи складніше, так що метод (7.29) вимагає на кожному кроці трохи більшого обсягу обчислень. Перевага різницевої схеми Кранка-Ніколсона полягає в тому, що вона не тільки є безумовно стійкої, як і різницева схема (5.25), але і має другий порядок точності як за просторовою змінною, так і за часом.

Розглянемо хід обчислювального процесу. На нульовому часовому шарі значення задані початковими умовами (2.13): . Щоб знайти , необхідно вирішити систему лінійних рівнянь (7.30) при k=0. Вирішити цю систему можна методом прогону. Умови стійкості прогону тут виконані — матриця коефіцієнтів має діагональну перевагу. У результаті рішення знайдемо значення . Аналогічно знаходимо рішення для другого шару. Обчислювальний процес продовжуємо до досягнення m-го часового шару.

Збіжність рішень різницевих рівнянь до точного рішення и(х, t) забезпечує наступне твердження: якщо функція u(х, t) має всі похідні до четвертого порядку включно, то рішення різницевої схеми (7.29) при збігається до точного рішення і має місце оцінка

. (7.30.а)