1. Реляционная модель данных — логическая модель данных, прикладная теория построения баз данных, которая является приложением к задачам обработки данных таких разделов математики как теории множеств и логика первого порядка.

На реляционной модели данных строятся реляционные базы данных.

Реляционная модель данных включает следующие компоненты:

• Структурный аспект (составляющая) — данные в базе данных представляют собой набор отношений.

• Аспект (составляющая) целостности — отношения (таблицы) отвечают определенным условиям целостности. РМД поддерживает декларативные ограничения целостности уровня домена (типа данных), уровня отношения и уровня базы данных.

• Аспект (составляющая) обработки (манипулирования) — РМД поддерживает операторы манипулирования отношениями (реляционная алгебра, реляционное исчисление).

Кроме того, в состав реляционной модели данных включают теорию нормализации.

Термин «реляционный» означает, что теория основана на математическом понятии отношение (relation). В качестве неформального синонима термину «отношение» часто встречается слово таблица. Необходимо помнить, что «таблица» есть понятие нестрогое и неформальное и часто означает не «отношение» как абстрактное понятие, а визуальное представление отношения на бумаге или экране. Некорректное и нестрогое использование термина «таблица» вместо термина «отношение» нередко приводит к недопониманию. Наиболее частая ошибка состоит в рассуждениях о том, что РМД имеет дело с «плоскими», или «двумерными» таблицами, тогда как таковыми могут быть только визуальные представления таблиц. Отношения же являются абстракциями, и не могут быть ни «плоскими», ни «неплоскими».

Для лучшего понимания РМД следует отметить три важных обстоятельства:

• модель является логической, то есть отношения являются логическими (абстрактными), а не физическими (хранимыми) структурами;

• для реляционных баз данных верен информационный принцип: всё информационное наполнение базы данных представлено одним и только одним способом, а именно — явным заданием значений атрибутов в кортежах отношений; в частности, нет никаких указателей (адресов), связывающих одно значение с другим;

• наличие реляционной алгебры позволяет реализовать декларативное программирование и декларативное описание ограничений целостности, в дополнение к навигационному (процедурному) программированию и процедурной проверке условий.

• N-арным отношением R, или отношением R степени n, называют подмножество декартовa произведения множеств 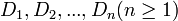 , не обязательно различных. Исходные множества D₁,D₂,...,D_n называют в модели доменами (в СУБД используется понятие тип данных).

Отношение имеет простую графическую интерпретацию, оно может быть представлено в виде таблицы, столбцы (поля, атрибуты) которой соответствуют вхождениям доменов в отношение, а строки (записи) — наборам из n значений, взятых из исходных доменов. Число строк (кортежей) n, называют кардиальным числом отношения, или мощностью отношения.

Такая таблица обладает рядом свойств:

1. В таблице нет двух одинаковых строк.

2. Таблица имеет столбцы, соответствующие атрибутам отношения.

3. Каждый атрибут в отношении имеет уникальное имя.

4. Порядок строк в таблице произвольный.

Под атрибутом здесь понимается вхождение домена в отношение. Строки отношения называются кортежами.

Далее следует формализованное определение введённых понятий.

• Заголовок Hr (или схема) отношения r — конечное множество упорядоченных пар вида <A, T>, где A называется именем атрибута, а T обозначает имя некоторого базового типа или ранее определенного домена, то есть множества допустимых значений. По определению требуется, чтобы все имена атрибутов в заголовке отношения были различны.

• Кортеж tr, соответствующий заголовку Hr — множество упорядоченных триплетов вида <A, T, v>, по одному такому триплету для каждого атрибута в Hr. Третий элемент – v– триплета <A, T, v> должен являться допустимым значением типа данных или домена T. Замечание: так как имена атрибутов уникальны, то указание домена в кортеже излишне.

• Тело Br отношения — неупорядоченное множество различных кортежей tr.

• Значением Vr отношения r называется пара множеств Hr и Br.

Полезно также понятие первичного ключа — это такой набор атрибутов, который однозначно определяет кортеж и минимален среди всех своих подмножеств (то есть нельзя убрать ни один из атрибутов). При добавлении новых записей первичный ключ обязан оставаться первичным ключом (например, неверным будет использование в качестве первичного ключа набора Имя + Отчество + Фамилия сотрудника, даже если на момент создания таблицы полных тёзок среди заносимых в неё людей не было).

Це́лостность ба́зы да́нных (database integrity) — соответствие имеющейся в базе данных информации её внутренней логике, структуре и всем явно заданным правилам. Каждое правило, налагающее некоторое ограничение на возможное состояние базы данных, называется ограничением целостности (integrity constraint). Примеры правил: вес детали должен быть положительным; количество знаков в телефонном номере не должно превышать 25; возраст родителей не может быть меньше возраста их биологического ребёнка и т.д.

Задача аналитика и проектировщика базы данных — возможно более полно выявить все имеющиеся ограничения целостности и задать их в базе данных.

Целостность БД не гарантирует достоверности содержащейся в ней информации, но обеспечивает по крайней мере правдоподобность этой информации, отвергая заведомо невероятные, невозможные значения. Таким образом, не следует путать целостность БД с достоверностью БД. Достоверность (или истинность) есть соответствие фактов, хранящихся в базе данных, реальному миру. Очевидно, что для определения достоверности БД требуется обладание полными знаниями как о содержимом БД, так и о реальном мире. Для определения целостности БД требуется лишь обладание знаниями о содержимом БД и о заданных для неё правилах. Поэтому СУБД может (и должна) контролировать целостность БД, но принципиально не в состоянии контролировать достоверность БД. Контроль достоверности БД может быть возложен только на человека, да и то в ограниченных масштабах, поскольку в ряде случаев люди тоже не обладают полнотой знаний о реальном мире.

Итак, БД может быть целостной, но не достоверной. Возможно и обратное: БД может быть достоверной, но не целостной. Последнее имеет место, если правила (ограничения целостности) заданы неверно.

Потенциальный ключ — в реляционной модели данных — подмножество атрибутов отношения, удовлетворяющее требованиям уникальности и минимальности (несократимости).

Уникальность означает, что не существует двух кортежей данного отношения, в которых значения этого подмножества атрибутов совпадают (равны).

Минимальность (несократимость) означает, что в составе потенциального ключа отсутствует меньшее подмножество атрибутов, удовлетворяющее условию уникальности. Иными словами, если из потенциального ключа убрать любой атрибут, он утратит свойство уникальности.

Поскольку все кортежи в отношении по определению уникальны, в нём всегда существует хотя бы один потенциальный ключ (например, включающий все атрибуты отношения).

В отношении может быть одновременно несколько потенциальных ключей. Один из них может быть выбран в качестве первичного ключа отношения, тогда другие потенциальные ключи называют альтернативными ключами

Теоретически, все потенциальные ключи равно пригодны в качестве первичного ключа, на практике в качестве первичного обычно выбирается тот из потенциальных ключей, который имеет меньший размер (физического хранения) и/или включает меньшее количество атрибутов.

Перви́чный ключ (англ. primary key) — в реляционной модели данных один из потенциальных ключей отношения, выбранный в качестве основного ключа (или ключа по умолчанию).

Если в отношении имеет единственный потенциальный ключ, он является и первичным ключом. Если потенциальных ключей несколько, один из них выбирается в качестве первичного, а другие называют «альтернативными».

С точки зрения теории все потенциальные ключи отношения эквивалентны, то есть обладают одинаковыми свойствами уникальности и минимальности. Однако в качестве первичного обычно выбирается тот из потенциальных ключей, который наиболее удобен для тех или иных практических целей, например для создания внешних ключей в других отношениях либо для создания кластерного индекса. Поэтому в качестве первичного ключа как правило выбирают тот, который имеет наименьший размер (физического хранения) и/или включает наименьшее количество атрибутов.

Исторически термин «первичный ключ» появился и стал использоваться существенно ранее термина «потенциальный ключ». Вследствие этого множество определений в реляционной теории были изначально сформулированы с упоминанием первичного (а не потенциального) ключа, например, определения нормальных форм. Так же термин «первичный ключ» вошёл в формулировку 12 правил Кодда как основной способ адресации любого значения отношения (таблицы) наряду с именем отношения (таблицы) и именем атрибута (столбца).

Первичный ключ в таблице является базовым уникальным идентификатором для записей. Значение первичного ключа используется везде, где нужно указать на конкретную запись. На использовании первичных ключей основана организация связей между таблицами реляционной БД. Чтобы организовать между двумя таблицами связь типа «один к одному» или «один ко многим (многие к одному)» в одну из связываемых таблиц добавляют поле (поля), содержащее (-ие) значение первичного ключа записи в связанной таблице (такое поле называют внешним ключом). Для организации связи типа «многие ко многим» создают отдельную таблицу (так называемую «таблицу связи» или «таблицу ассоциации»), каждая запись которой содержит первичные ключи двух связанных записей в разных таблицах.

Реляционная алгебра — формальная система манипулирования отношениями в реляционной модели данных. Существует в двух несколько различающихся вариантах:

• алгебра Кодда (Э. Кодд, 1970)

• алгебра A (К. Дейт, Х. Дарвен)

Наряду с реляционным исчислением является способом получения результирующего отношения в реляционной модели данных.

Замкнутость реляционной алгебры

Реляционная алгебра представляет собой набор операторов, использующих отношения в качестве аргументов и возвращающих отношения в качестве результата. Таким образом, реляционный оператор f выглядит как функция с отношениями в качестве аргументов: R = f(R₁, R₂, …, R_n) Реляционная алгебра является замкнутой, так как в качестве аргументов в реляционные операторы можно подставлять другие реляционные операторы, подходящие по типу: R = f(f₁(R₁₁, R₁₂, …), f₂(R₂₁, R₂₂,…),…) В реляционных выражениях можно использовать вложенные выражения сколь угодно сложной структуры. Каждое отношение обязано иметь уникальное имя в пределах базы данных. Имя отношения, полученного в результате выполнения реляционной операции, определяется в левой части равенства. Однако можно не требовать наличия имён от отношений, полученных в результате реляционных выражений, если эти отношения подставляются в качестве аргументов в другие реляционные выражения. Такие отношения называют неименованными отношениями. Неименованные отношения реально не существуют в базе данных, а только вычисляются в момент вычисления значения реляционного оператора.

Реляционное исчисление — прикладная ветвь формального механизма исчисления предикатов первого порядка. В основе исчисления лежит понятие переменной с определенной для нее областью допустимых значений и понятие правильно построенной формулы, опирающейся на переменные, предикаты и кванторы. Наряду с реляционной алгеброй является способом получения результирующего отношения в реляционной модели данных. В зависимости от того, что является областью определения переменной, различают:

Правильно построенные формулы

Правильно построенная формула (Well-Formed Formula, WFF) служит для выражения условий, накладываемых на кортежные переменные.

Простые условия

Простые условия представляют собой операции сравнения скалярных значений. Примеры:

ИмяПеременной. ИмяАтрибута = СкалярноеЗначение

ИмяПеременнойА.ИмяАтрибутаБ = ИмяПеременнойВ.ИмяАтрибутаГ

ИмяПеременной. ИмяАтрибута <> СкалярноеЗначение

ИмяПеременнойА.ИмяАтрибутаБ < ИмяПеременнойВ.ИмяАтрибутаГ

Сложные условия

Сложные условия строятся с помощью логических связок NOT, AND, OR и IF … THEN с учетом обычных приоритетов операций (NOT > AND > OR) и возможности расстановки скобок. Так, если Формула — правильно построенная формула, а Условие — простое сравнение, то

NOT Формула

Условие AND Формула

Условие OR Формула

IF Условие THEN Формула

являются правильно построенными формулами.

2. Операции реляционной алгебры

Теоретико-множественные операторы

Объединение

Отношение с тем же заголовком, что и у совместимых по типу отношений A и B, и телом, состоящим из кортежей, принадлежащих или A, или B, или обоим отношениям. Синтаксис: A UNION B

Пересечение

Отношение с тем же заголовком, что и у отношений A и B, и телом, состоящим из кортежей, принадлежащих одновременно обоим отношениям A и B. Синтаксис: A INTERSECT B

Вычитание

Отношение с тем же заголовком, что и у совместимых по типу отношений A и B, и телом, состоящим из кортежей, принадлежащих отношению A и не принадлежащих отношению B. Синтаксис: A MINUS B

Декартово произведение

Отношение (A₁, A₂, …, A_m, B₁, B₂, …, B_m), заголовок которого является сцеплением заголовков отношений A(A₁, A₂, …, A_m) и B(B₁, B₂, …, B_m), а тело состоит из кортежей, являющихся сцеплением кортежей отношений A и B:

(a₁, a₂, …, a_m, b₁, b₂, …, b_m)

таких, что (a₁, a₂, …, a_m)∈ A, (b₁, b₂, …, b_m)∈ B.

Синтаксис:

A TIMES B

Селекция - Отношение с тем же заголовком, что и у отношения A, и телом, состоящим из кортежей, значения атрибутов которых при подстановке в условие c дают значение ИСТИНА. cпредставляет собой логическое выражение, в которое могут входить атрибуты отношения A и/или скалярные выражения. Синтаксис: A WHERE c

Проекция в реляционной алгебре — унарная операция, которая позволяет получить «вертикальное» подмножество данного отношения, или таблицы, то есть такое подмножество, которое получается выбором специфицированных атрибутов с последующим исключением, если это необходимо, избыточных дубликатов кортежей. Пусть дана таблица T с атрибутами  , то есть   и некоторое подмножество множества атрибутов  . Результатом проекции таблицы по выбранным атрибутам называется новая таблица  , полученная из исходной таблицы вычеркиванием атрибутов, не входящих в выбранное множество, с последующим возможным удалением избыточных дубликатов кортежей.

При осуществление проекции необходимо задать проецируемое отношение и некий набор его атрибутов, который станет заголовком результирующего.

Соединение

Операция соединения есть результат последовательного применения операций декартового произведения и выборки. Если в отношениях и имеются атрибуты с одинаковыми наименованиями, то перед выполнением соединения такие атрибуты необходимо переименовать. Синтаксис: (A TIMES B) WHERE c

Деление

Отношение с заголовком (X₁, X₂, …, X_n) и телом, содержащим множество кортежей (x₁, x₂, …, x_n), таких, что для всех кортежей (y₁, y₂, …, y_m) ∈ B в отношении A(X₁, X₂, …, X_n, Y₁, Y₂, …, Y_m) найдется кортеж (x₁, x₂, …, x_n, y₁, y₂, …, y_m). Синтаксис: A DIVIDEBY B

3.

Нормальная форма — свойство отношения в реляционной модели данных, характеризующее его с точки зрения избыточности, которая потенциально может привести к логически ошибочным результатам выборки или изменения данных. Нормальная форма определяется как совокупность требований, которым должно удовлетворять отношение.

Процесс преобразования базы данных к виду, отвечающему нормальным формам, называется нормализацией. Нормализация предназначена для приведения структуры базы данных к виду, обеспечивающему минимальную избыточность, то есть нормализация не имеет целью уменьшение или увеличение производительности работы или же уменьшение или увеличение объёма БД. Конечной целью нормализации является уменьшение потенциальной противоречивости хранимой в БД информации.

Устранение избыточности производится, как правило, за счёт декомпозиции отношений таким образом, чтобы в каждом отношении хранились только первичные факты (то есть факты, не выводимые из других хранимых фактов).

Первая нормальная форма (1NF)

Определение

Таблица находится в первой нормальной форме, если каждый её атрибут атомарен, то есть может содержать только одно значение. Таким образом, не существует 1NF таблицы, в полях которых могут храниться списки значений. Для приведения таблицы к 1NF обычно требуется разбить таблицу на несколько отдельных таблиц.

Замечание: в реляционной модели отношение всегда находится в 1 (или более высокой) нормальной форме в том смысле, что иные отношения не рассматриваются в реляционной модели. То есть само определение понятия отношение заведомо подразумевает наличие 1NF.

Пример

Пример приведения таблицы к первой нормальной форме

Исходная, ненормализованная, таблица:

Сотрудник	Номер телефона
Иванов И. И.	283-56-82 390-57-34
Петров П. Ю.	708-62-34

Таблица, приведённая к 1NF:

Сотрудник	Номер телефона
Иванов И. И.	283-56-82
Иванов И. И.	390-57-34
Петров П. Ю.	708-62-34

Атомарность атрибутов

Вопрос об атомарности атрибутов решается на основе семантики данных, то есть их смыслового значения. Атрибут атомарен, если его значение теряет смысл при любом разбиении на части или переупорядочивании. И наоборот, если какой-либо способ разбиения на части не лишает атрибут смысла, то атрибут неатомарен.

Одно и то же значение может быть атомарным или неатомарным в зависимости от смысла этого значения. Например, значение «4286» является

• атомарным, если его смысл — «пин-код кредитной карты» (при разбиении на части или переупорядочивании смысл теряется)

• неатомарным, если его смысл — «четные цифры» (при разбиении на части или переупорядочивании смысл не теряется)

Хорошим способом принятия решения о необходимости разбиения атрибута на части является вопрос: «будут ли части атрибута использоваться по отдельности?». Если да, то атрибут следует разделить (но так, чтобы сохранились осмысленные части атрибута). Далее необходимо снова задаться тем же вопросом для новой структуры и так до тех пор, пока не останется атрибутов, допускающих разбиение.

Примеры неатомарного атрибута, часто встречающиеся на практике: составные поля в виде строки идентификаторов, разделённых, скажем, запятыми: 100,32,168,1045

Вторая нормальная форма (2NF)