Тема 7.2. Классическое определение вероятности

 Вероятностью события А называется отношение числа исходов, благоприятствующих событию А к числу всех исходов.

Р(А) =

Пример 1. В урне 18 шаров, имеющих номера: 1, 2, …, 18. Наугад вынутый шар в своем номере имеет цифру 3 с вероятностью, равной …

а) б)

в) г)

Решение:

Вероятность того, что наугад вынутый шар в своем номере имеет цифру 3 равна Р(А) = 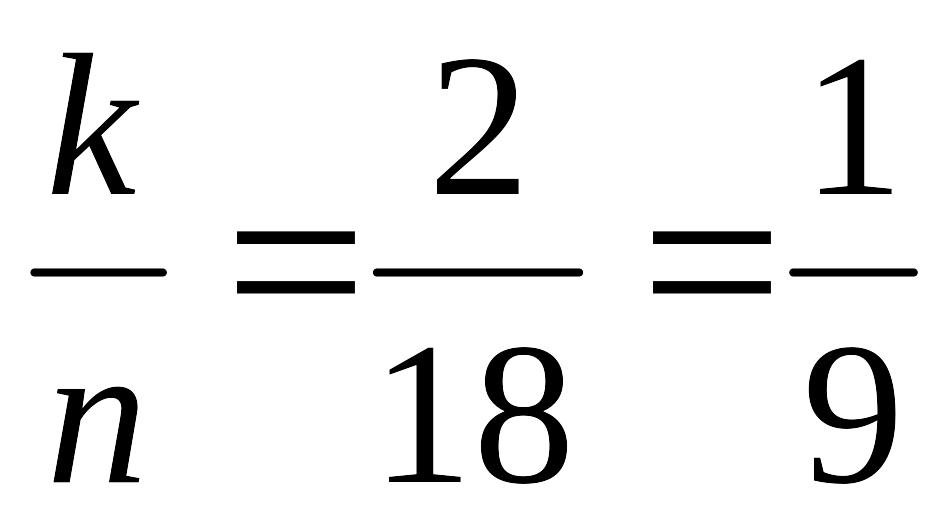, так как благоприятствующих исходов два – вынут шар с номером «3» или с номером «13», то есть k = 2, а всего исходов 18 – по числу шаров, то есть n = 18.

Ответ: б).

Задание 1. В урне 10 шаров, имеющих номера: 1, 2, …, 10. Наугад вынутый шар имеет номер, кратный 3, с вероятностью, равной …

а) б)

в) г)

_{Ответ: г).}

Задание 2. Среди 200 изделий встречается 15 нестандартных. Наугад взятое изделие окажется нестандартным с вероятностью, равной …

а) б)

в) г)

_{Ответ: б).}

Задание 3. В урне 10 шаров, имеющих номера: 1, 2, …, 10. Наугад вынутый шар имеет номер, больший 4, с вероятностью, равной …

а) б)

в) г)

_{Ответ: в).}

Задание 4. В урне 35 белых и 55 черных шаров. Наугад вынутый шар окажется белым с вероятностью, равной …

а) б)

в) г)

Ответ: а).

Тема 7.3. Характеристики вариационного ряда Выборочное среднее

xi	1	2	3	4
ni	225	280	320	125

Пример 1. Объём выборки, заданной статистическим распределением (см. таблицу), равен …

Решение:

Случайная величина Х принимает некоторое значение 225 раз, второе значение − 280 раз, третье значение − 320 раз и четвертое значение – 125 раз. Тогда n = 225 + 280 + + 320 + 125 = 950 – объём выборки.

Ответ: 950.

xi	1	2	3	4
ni	25	22	18	15

Задание 1. Объём выборки, заданной статистическим распределением (см. таблицу), равен …

Ответ: 80.

xi	1	2	3	4
ni	120	180	205	95

Задание 2. Объем выборки, заданной статистическим распределением (см. таблицу), равен …

Ответ: 600.

xi	1	4	8	10
ni	2	2	5	1

Пример 2. Выборочное среднее для вариационного ряда (см. таблицу) равно…

Решение:

Выборочным средним называется среднее арифметическое всех значений выборки: Обращаем внимание, что значение «1» заданная случайная величина принимает 2 раза, значение «4» – 2 раза, значение «8» – 5 раз и значение «10» − 1 раз. Тогда среднее арифметическое всех значений выборки равно

Ответ: 6.

xi	5	7	8	10
ni	2	3	1	1

Пример 3. Выборочное среднее для вариационного ряда (см. таблицу) равно…

Решение:

Выборочным средним называется среднее арифметическое всех значений выборки: Обращаем внимание, что значение «5» заданная случайная величина принимает 2 раза, значение «7» – 3 раза, значение «8» – 1 раз и значение «10» − 1 раз. Тогда среднее арифметическое всех значений выборки равно

Ответ: 7.

xi	1	5	7	10
ni	1	3	2	4

Задание Выборочное среднее для вариационного ряда (см. таблицу) равно …

Ответ: 7.