
- •Учебно-методическое пособие для подготовки к интернет-тестированию по математике
- •Содержание
- •Введение
- •Основы линейной алгебры
- •Тема 1.1. Действия над матрицами
- •Тема 1.2. Определители второго порядка
- •Тема 1.3. Системы линейных уравнений
- •2. Дифференциальное исчисление
- •Тема 2.1. Правила дифференцирования
- •Тема 2.2. Производная сложной функции
- •Тема 2.3. Производная функции в точке
- •Тема 2.4. Экстремум функции
- •Тема 2.5. Наибольшее и наименьшее значения функции на отрезке
- •3. Интегральное исчисление
- •Тема 3.1. Неопределенный интеграл
- •Тема 3.2. Методы вычисления неопределенных интегралов
- •Тема 3.3. Определенный интеграл
- •Тема 3. 4. Свойства определенного интеграла
- •Тема 3.5. Геометрические приложения определенного интеграла
- •4. Дифференциальные уравнения
- •Тема 4.1. Основные понятия теории дифференциальных уравнений
- •Тема 4.2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- •Тема 4.3. Линейные дифференциальные уравнения первого порядка
- •Тема 4.4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •5. Ряды
- •Тема 5.1. Числовые ряды
- •Тема 5.2. Сумма числового ряда
- •Тема 5.3. Степенные ряды
- •6. Основы дискретной математики
- •Тема 6.1. Числовые множества. Основные понятия теории множеств
- •Тема 6.2. Действия над множествами
- •Тема 6.3. Прямое произведение двух множеств
- •Тема 6.4. Способы задания множеств, конечные и бесконечные множества
- •7. Основы теории вероятностей и математической статистики
- •Тема 7.1. Элементы комбинаторики
- •Тема 7.2. Классическое определение вероятности
- •Тема 7.3. Характеристики вариационного ряда Выборочное среднее
- •Тема 7.4. Математическое ожидание дискретной случайной величины
- •8. Основные численные методы
- •Тема 8.1. Приближенные числа и действия над ними
- •Тема 8.2. Понятие конечных разностей функции
- •Тема 8.3. Численное дифференцирование
- •Тема 8.4. Численное интегрирование
- •Тема 8.5. Приближенное решение обыкновенных дифференциальных уравнений
- •9. Основы теории комплексных чисел
- •Тема 9.1. Модуль и аргумент комплексного числа
- •Тема 9.2. Сопряженные комплексные числа
- •Тема 9.3. Действия над комплексными числами в алгебраической форме
- •Тема 9.4. Тригонометрическая форма комплексного числа
- •Тема 9.5. Показательная форма комплексного числа
- •Тема 9.6. Решение уравнений
- •10. Теория пределов
- •Тема 10.1. Предел функции в точке
- •Тема 10.2. Первый замечательный предел
- •Тема.10.3. Второй замечательный предел
- •Тема 10.4. Раскрытие неопределенности вида "бесконечность на бесконечность"
- •Тема 10.5. Раскрытие неопределенности вида "ноль на ноль"
- •Модуль 1. Основы линейной алгебры
- •Модуль 2. Основы дифференциального исчисления Производная сложной функции
- •Модуль 3. Определенный интеграл
- •Модуль 4. Применение производной функции
- •Модуль 5. Применение определённого интеграла
- •Модуль 6. Ряды Необходимый признак сходимости ряда
- •Модуль 7. Основы дискретной математики
- •Модуль 8. Основы теории вероятностей и математической статистики Теоремы сложения и умножения вероятностей
- •Модуль 9. Основы теории комплексных чисел Тригонометрическая форма комплексного числа
- •Показательная форма комплексного числа
- •Справочный материал
- •1.Основные значения тригонометрических функций
- •2. Таблица производных
- •3.Таблица интегралов
- •Библиография
3. Интегральное исчисление
Тема 3.1. Неопределенный интеграл
?Пример
1.
Неопределенный интеграл ![]() равен …
равен …
а)
![]()
б)
![]()
в)
![]()
г)
![]() .
.
Решение:
Напоминаем,
что постоянный множитель можно выносить
за знак неопределенного интеграла:
Тогда, ![]() и, используя формулу
и, используя формулу ![]() ,
получим:.
,
получим:.![]() .
.
Ответ:
![]()
?Пример
2.
Неопределенный интеграл ![]() равен …
равен …
а)
![]()
б)![]()
в)![]()
г)
![]() .
.
Решение:
Напоминаем,
что интеграл суммы двух функций равен
сумме интегралов этих функций и
постоянный множитель можно выносить
за знак неопределенного интеграла:
Тогда, ![]() и, используя формулы
и, используя формулы ![]() и
и ![]() ,
получим:
,
получим: ![]() .
.
Ответ:
![]()
![]()
Задание
Неопределенный
интеграл ![]() равен …
равен …
Ответ:
![]()
Тема 3.2. Методы вычисления неопределенных интегралов
?Пример
1.
Неопределенный интеграл ![]() равен …
равен …
а)
![]()
б)![]()
в)![]()
г)
![]()
Решение:
Напоминаем,
что табличный интеграл
![]() .
Но так как в исходном интеграле перед
аргументом х
стоит коэффициент
.
Но так как в исходном интеграле перед
аргументом х
стоит коэффициент
![]() ,
то по формуле
,
то по формуле
![]() получаем:
получаем:
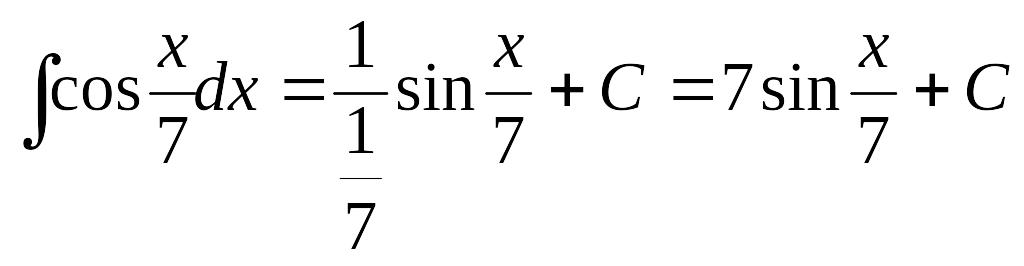 .
.
Ответ: б).
?Пример
2.
Неопределенный интеграл ![]() равен …
равен …
а)
![]()
б)![]()
в)![]()
г)
![]()
Решение:
Подстановка
5x
+ 1 = t
приводит рассматриваемый интеграл к
табличному: ![]() Найдем
дифференциал от обеих частей подстановки:
5dx
= dt,
тогда
Найдем
дифференциал от обеих частей подстановки:
5dx
= dt,
тогда ![]() Подставим получившиеся выражения в
исходный интеграл:
Подставим получившиеся выражения в
исходный интеграл: ![]() Заменив
t
его
выражением из подстановки, получим:
Заменив
t
его
выражением из подстановки, получим:
![]() .
.
Ответ: а) .
Задание
Неопределенный
интеграл ![]() равен …
равен …
а)
![]()
б)
![]()
в)
![]()
г)
![]()
Ответ: г).
Тема 3.3. Определенный интеграл
?Пример
1.
Определённый интеграл ![]() равен …
равен …
Решение:
Используя
табличную формулу ![]() и формулу Ньютона – Лейбница
и формулу Ньютона – Лейбница ![]() ,
получим:
,
получим: ![]() .
.
Ответ: 10.
?Пример
2.
Определённый
интеграл ![]() равен …
равен …
Решение:
Используя
свойства определённого интеграла ![]() ,
и свойства степени
,
и свойства степени ![]() и
и ![]() исходный интеграл можно представить
в виде:
исходный интеграл можно представить
в виде:
![]() и, применяя табличную формулу
и формулу Ньютона – Лейбница
,
получим:
и, применяя табличную формулу
и формулу Ньютона – Лейбница
,
получим: ![]()
 .
.
Ответ: 20
Задание
1.
Определенный
интеграл ![]() равен …
равен …
Ответ: 9.
Задание
2.
Определенный
интеграл ![]() равен …
равен …
Ответ: 18
Тема 3. 4. Свойства определенного интеграла
?Пример
1.
Определённый
интеграл ![]() равен …
равен …
Решение:
Используя
свойства определённого интеграла ![]() и
,
исходный интеграл можно представить в
виде разности двух выражений и, применяя
формулу Ньютона – Лейбница
и
,
исходный интеграл можно представить в
виде разности двух выражений и, применяя
формулу Ньютона – Лейбница ![]() ,
получим:
,
получим:
 .
.
Ответ: 60.
èЗадание
Определенный
интеграл
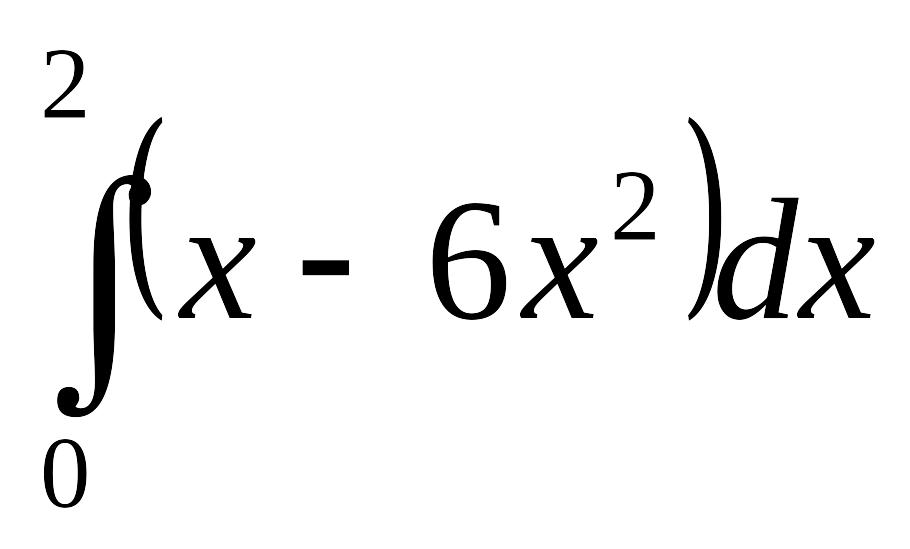 равен …
равен …
Ответ:
![]() 14.
14.
Тема 3.5. Геометрические приложения определенного интеграла
Определённый
интеграл
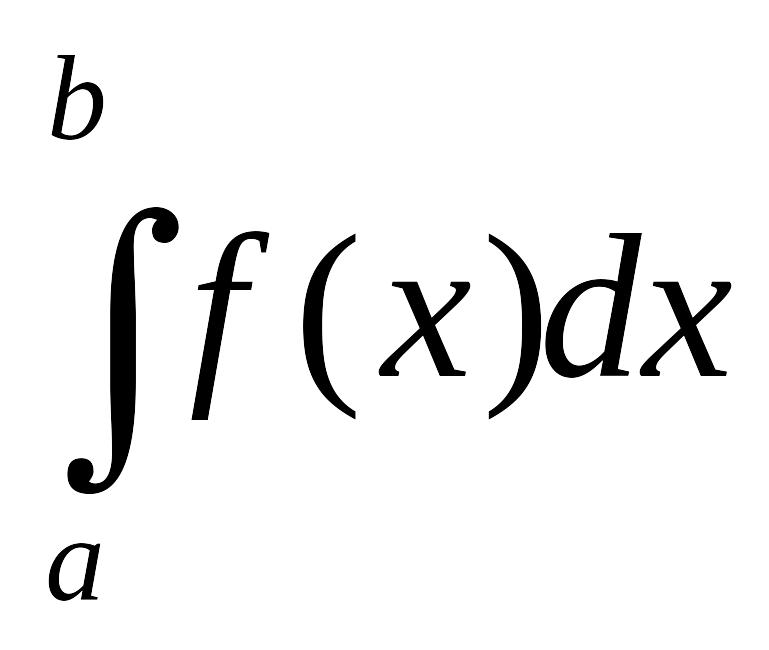 равен площади криволинейной трапеции,
ограниченной графиком функции
равен площади криволинейной трапеции,
ограниченной графиком функции
![]() ,
осью абсцисс OX
и вертикальными прямыми х
= а
и х
= в (см.
рис. 1).
,
осью абсцисс OX
и вертикальными прямыми х
= а
и х
= в (см.
рис. 1).

![]()
?Пример
1.
Площадь криволинейной трапеции,
ограниченной графиком функции ![]() ,
прямыми x
= 1, x
= 3, и осью абсцисс, равна …
,
прямыми x
= 1, x
= 3, и осью абсцисс, равна …
Решение:
Площадь
плоской фигуры вычисляется по формуле
![]() Тогда
получаем:
Тогда
получаем:  .
.
Ответ: S = 80 кв. ед.
èЗадание
Площадь
фигуры, ограниченной графиком функции
![]() ,
прямыми x
= 1, x
= 2, и осью абсцисс, равна …
,
прямыми x
= 1, x
= 2, и осью абсцисс, равна …
Ответ: S = 14 кв. ед.
4. Дифференциальные уравнения
Тема 4.1. Основные понятия теории дифференциальных уравнений
& Определение 1. Дифференциальным уравнением называют уравнение, содержащее переменную х, искомую функцию у = у(х) и её производные.
& Определение 2. Решением дифференциального уравнения называют всякую функцию, обращающую данное уравнение в тождество.
Существуют два вида решений дифференциального уравнения: общее решение и частные решения. Общее решение дифференциального уравнения зависит от произвольных постоянных С1, С2, … Частные решения получаются из общего при конкретном значении этих постоянных.
?Пример
1.
Частными решениями дифференциального
уравнения
![]() являются …
являются …
а)
![]() б)
б)
![]()
в)
![]() г)
г)
![]()
Решение:
Можно проверить каждую из данных функций.
а)
![]() .
После подстановки в уравнение получим
.
После подстановки в уравнение получим
![]() .
Значит,
является
решением уравнения.
.
Значит,
является
решением уравнения.
б)
![]() .
После подстановки в уравнение получим
.
После подстановки в уравнение получим
![]() .
Значит,
является
решением уравнения.
.
Значит,
является
решением уравнения.
в)
![]() .
После подстановки в уравнение получим
.
После подстановки в уравнение получим
![]() .
Значит,
не
является решением уравнения.
.
Значит,
не
является решением уравнения.
г)
![]() .
После подстановки в уравнение получим
.
После подстановки в уравнение получим
![]() .
Значит,
не
является решением уравнения.
.
Значит,
не
является решением уравнения.
Ответ: а) и б).
èЗадание
1.
Частным
решением дифференциального уравнения
![]() является …
является …
а)
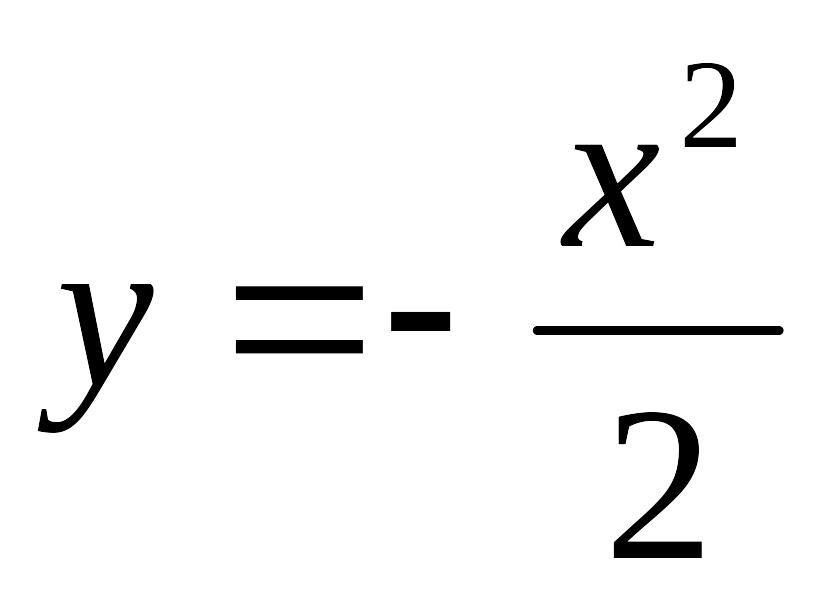 б)
б)
![]()
в)
![]() г)
г)
![]()
Ответ: в).
èЗадание
2.
Частными
решениями дифференциального уравнения
![]() являются
…
являются
…
а)
![]() б)
б)
![]()
в)
![]() г)
г)
Ответ: а) и б).
èЗадание
3.
Функция
![]() является решением дифференциального
уравнения
является решением дифференциального
уравнения
![]() .
Чему равна константа С
?
.
Чему равна константа С
?
а) 1 б) – 1
в)
![]() г)
2
г)
2
Ответ: г).
?Пример 2. Дифференциальным уравнением в частных производных является …
а)
![]() б)
б)
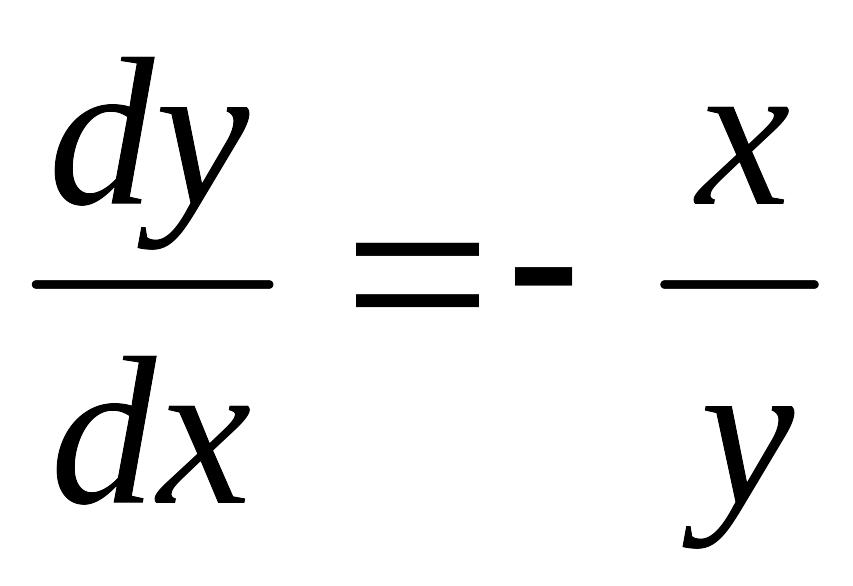
в)
![]() г)
г)
![]()
Решение:
Так
как частные производные – это производные
от функции нескольких переменных, для
функции f(x;y)
они обозначаются
![]() и
и
![]() ,
то уравнение в частных производных:
.
,
то уравнение в частных производных:
.
Ответ: г).
