
- •Учебно-методическое пособие для подготовки к интернет-тестированию по математике
- •Содержание
- •Введение
- •Основы линейной алгебры
- •Тема 1.1. Действия над матрицами
- •Тема 1.2. Определители второго порядка
- •Тема 1.3. Системы линейных уравнений
- •2. Дифференциальное исчисление
- •Тема 2.1. Правила дифференцирования
- •Тема 2.2. Производная сложной функции
- •Тема 2.3. Производная функции в точке
- •Тема 2.4. Экстремум функции
- •Тема 2.5. Наибольшее и наименьшее значения функции на отрезке
- •3. Интегральное исчисление
- •Тема 3.1. Неопределенный интеграл
- •Тема 3.2. Методы вычисления неопределенных интегралов
- •Тема 3.3. Определенный интеграл
- •Тема 3. 4. Свойства определенного интеграла
- •Тема 3.5. Геометрические приложения определенного интеграла
- •4. Дифференциальные уравнения
- •Тема 4.1. Основные понятия теории дифференциальных уравнений
- •Тема 4.2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- •Тема 4.3. Линейные дифференциальные уравнения первого порядка
- •Тема 4.4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •5. Ряды
- •Тема 5.1. Числовые ряды
- •Тема 5.2. Сумма числового ряда
- •Тема 5.3. Степенные ряды
- •6. Основы дискретной математики
- •Тема 6.1. Числовые множества. Основные понятия теории множеств
- •Тема 6.2. Действия над множествами
- •Тема 6.3. Прямое произведение двух множеств
- •Тема 6.4. Способы задания множеств, конечные и бесконечные множества
- •7. Основы теории вероятностей и математической статистики
- •Тема 7.1. Элементы комбинаторики
- •Тема 7.2. Классическое определение вероятности
- •Тема 7.3. Характеристики вариационного ряда Выборочное среднее
- •Тема 7.4. Математическое ожидание дискретной случайной величины
- •8. Основные численные методы
- •Тема 8.1. Приближенные числа и действия над ними
- •Тема 8.2. Понятие конечных разностей функции
- •Тема 8.3. Численное дифференцирование
- •Тема 8.4. Численное интегрирование
- •Тема 8.5. Приближенное решение обыкновенных дифференциальных уравнений
- •9. Основы теории комплексных чисел
- •Тема 9.1. Модуль и аргумент комплексного числа
- •Тема 9.2. Сопряженные комплексные числа
- •Тема 9.3. Действия над комплексными числами в алгебраической форме
- •Тема 9.4. Тригонометрическая форма комплексного числа
- •Тема 9.5. Показательная форма комплексного числа
- •Тема 9.6. Решение уравнений
- •10. Теория пределов
- •Тема 10.1. Предел функции в точке
- •Тема 10.2. Первый замечательный предел
- •Тема.10.3. Второй замечательный предел
- •Тема 10.4. Раскрытие неопределенности вида "бесконечность на бесконечность"
- •Тема 10.5. Раскрытие неопределенности вида "ноль на ноль"
- •Модуль 1. Основы линейной алгебры
- •Модуль 2. Основы дифференциального исчисления Производная сложной функции
- •Модуль 3. Определенный интеграл
- •Модуль 4. Применение производной функции
- •Модуль 5. Применение определённого интеграла
- •Модуль 6. Ряды Необходимый признак сходимости ряда
- •Модуль 7. Основы дискретной математики
- •Модуль 8. Основы теории вероятностей и математической статистики Теоремы сложения и умножения вероятностей
- •Модуль 9. Основы теории комплексных чисел Тригонометрическая форма комплексного числа
- •Показательная форма комплексного числа
- •Справочный материал
- •1.Основные значения тригонометрических функций
- •2. Таблица производных
- •3.Таблица интегралов
- •Библиография
2. Дифференциальное исчисление
Тема 2.1. Правила дифференцирования
Пример
1.
Производная функции
![]() равна …
равна …
а)
![]()
б)
![]()
в)
![]()
г)
![]()
Решение:
Для
нахождения производной необходимо
воспользоваться правилами
![]() ,
,
![]() ,
,
![]() ,
где c
– постоянная величина, а u
и
v
– некоторые функции, зависящие от x,
и формулами
,
где c
– постоянная величина, а u
и
v
– некоторые функции, зависящие от x,
и формулами
![]() и
и
![]() .
.
Тогда
получим:
![]()
![]()
Ответ: в).
Пример
2.
Производная функции![]() равна …
равна …
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]() .
.
Решение:
Для
нахождения производной необходимо
воспользоваться правилами
,
,
,
где c
– постоянная величина, а u
и
v
– некоторые функции, зависящие от x,
и формулами
и
![]() .
.
Тогда
получим:
![]()
![]()
Ответ: а).
Задание
1.
Найдите производную функции:
![]()
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г)
![]()
Ответ: г).
Задание 2. Найдите производную функции:
Тема 2.2. Производная сложной функции
?Пример
1.
Найдите производную сложной функции:
![]() .
.
Решение:
Данная
функция является сложной. Пусть
![]() ,
тогда
,
тогда
![]() .
Напоминаем, что производная сложной
функции находится по формуле
.
Напоминаем, что производная сложной
функции находится по формуле
![]() .
Тогда получим
.
Тогда получим
![]() .
.
Ответ:
![]() .
.
Задание Найдите производную сложной функции:
Ответы:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
;
6)
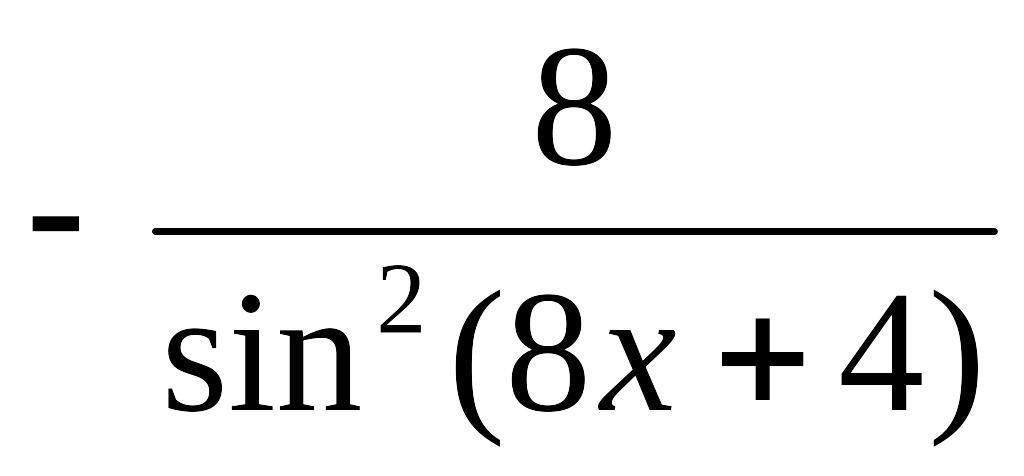 ;
7)
;
7)
![]() ; 8)
; 8)
![]() ; 9)
; 9)
![]() .
.
Тема 2.3. Производная функции в точке
?Пример
1.
Если![]() ,
то
,
то
![]() принимает значение, равное …
принимает значение, равное …
Решение:
Производная
суммы двух функций равна сумме производных
этих функций, значит,
![]() .
Пусть х
=
0. Тогда
.
Пусть х
=
0. Тогда
![]() .
.
Ответ: 1.
?Пример
2.
Если![]() ,
то
принимает значение, равное …
,
то
принимает значение, равное …
Решение:
Напоминаем, что производная суммы двух функций равна сумме производных этих функций. Тогда имеем:
![]() .
.
Пусть
х
=
0. Получим
![]() .
.
Ответ: 6.
Задание
1.
Если
![]() ,
то
принимает значение, равное …
,
то
принимает значение, равное …
Ответ: 4.
Задание
2.
Если
![]() ,
то
,
то
![]()
Ответ: – 4.
Задание
3. Если
![]() ,
то
,
то
![]() принимает значение, равное…
принимает значение, равное…
Ответ: 1.
Задание
4.
Если
![]() ,
то
,
то
![]() принимает значение, равное…
принимает значение, равное…
Ответ: 3.
Тема 2.4. Экстремум функции
Пример
1.
Для функции ![]() точка минимума x0
равна …
точка минимума x0
равна …
Решение:
Для
отыскания точек экстремума найдем
точки, в которых производная равна нулю
или не существует. ![]() .
Заметим,
что производная существует для любого
значения х,
приравняем ее к нулю, получим:
.
Заметим,
что производная существует для любого
значения х,
приравняем ее к нулю, получим: ![]()

![]() .
Последнее уравнение имеет корни: x
= 2, x
= 5. Отметим найденные значения на числовой
прямой. Найдем знак производной
.
Последнее уравнение имеет корни: x
= 2, x
= 5. Отметим найденные значения на числовой
прямой. Найдем знак производной ![]() на каждом из получившихся промежутков.
Точки x
= 2 и x
= 5 являются экстремальными, так как при
переходе через эти точки производная
меняет знак.
x0
= 5 – точка минимума, так как производная
меняет знак с «−» на «+».
на каждом из получившихся промежутков.
Точки x
= 2 и x
= 5 являются экстремальными, так как при
переходе через эти точки производная
меняет знак.
x0
= 5 – точка минимума, так как производная
меняет знак с «−» на «+».
Ответ: 5.
Задание
1.
Для
функции ![]() точка максимума x0
равна
…
точка максимума x0
равна
…
Ответ: 3.
Задание
2.
Найдите
точку минимума функции:
![]() .
.
Ответ: 5.
Задание
3.
Найдите
точку максимума функции:
![]() .
.
Ответ: 3.
Задание
4.
Найдите
точку минимума функции:
![]() .
.
Ответ: 1.
Задание
5.
Найдите
точку максимума функции:
![]() .
.
Ответ: – 6.
Тема 2.5. Наибольшее и наименьшее значения функции на отрезке
?Пример
1.
Наибольшее значение функции
на отрезке
![]() равно ….
равно ….
Решение:
Заметим,
что функция
![]() непрерывна на отрезке
.
Найдем значения функции на концах
отрезка:
непрерывна на отрезке
.
Найдем значения функции на концах
отрезка:
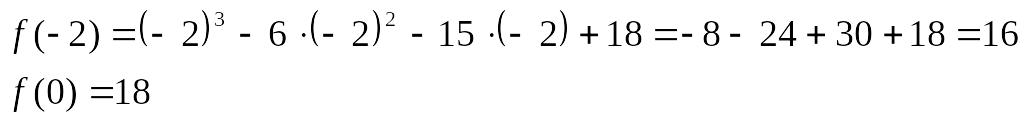
Найдём
производную данной функции:
![]() Тогда
Тогда
![]()
Так
как
![]() то
нужно найти только
то
нужно найти только
![]() .
.
![]() .
Сравнивая значения
.
Сравнивая значения
![]() ,
,
![]() и
и
![]() определим, что наибольшее значение
функции равно 26.
определим, что наибольшее значение
функции равно 26.
Ответ: 26.
?Пример
2.
Наименьшее значение функции
![]() на отрезке
на отрезке
![]() равно ….
равно ….
Решение:
Заметим, что функция непрерывна на отрезке . Найдем значения функции на концах отрезка:
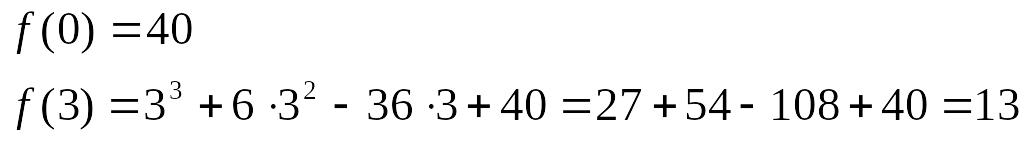
Найдём
производную данной функции:
![]() .
.
Тогда
![]()
Так
как
![]() то
нужно найти только
то
нужно найти только
![]() .
.
![]() .
Сравнивая значения
,
.
Сравнивая значения
,
![]() и
и
![]() определим, что наименьшее значение
функции равно 0.
определим, что наименьшее значение
функции равно 0.
Ответ: 0
Задание
1.
Найти
наименьшее значение функции
![]() на отрезке
на отрезке
![]() .
.
Задание
2.
Найти
наибольшее значение функции
![]() на отрезке
.
на отрезке
.
Задание
3.
Найдите
наименьшее значение функции
![]() на отрезке
на отрезке
![]()
