
- •Учебно-методическое пособие для подготовки к интернет-тестированию по математике
- •Содержание
- •Введение
- •Основы линейной алгебры
- •Тема 1.1. Действия над матрицами
- •Тема 1.2. Определители второго порядка
- •Тема 1.3. Системы линейных уравнений
- •2. Дифференциальное исчисление
- •Тема 2.1. Правила дифференцирования
- •Тема 2.2. Производная сложной функции
- •Тема 2.3. Производная функции в точке
- •Тема 2.4. Экстремум функции
- •Тема 2.5. Наибольшее и наименьшее значения функции на отрезке
- •3. Интегральное исчисление
- •Тема 3.1. Неопределенный интеграл
- •Тема 3.2. Методы вычисления неопределенных интегралов
- •Тема 3.3. Определенный интеграл
- •Тема 3. 4. Свойства определенного интеграла
- •Тема 3.5. Геометрические приложения определенного интеграла
- •4. Дифференциальные уравнения
- •Тема 4.1. Основные понятия теории дифференциальных уравнений
- •Тема 4.2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- •Тема 4.3. Линейные дифференциальные уравнения первого порядка
- •Тема 4.4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •5. Ряды
- •Тема 5.1. Числовые ряды
- •Тема 5.2. Сумма числового ряда
- •Тема 5.3. Степенные ряды
- •6. Основы дискретной математики
- •Тема 6.1. Числовые множества. Основные понятия теории множеств
- •Тема 6.2. Действия над множествами
- •Тема 6.3. Прямое произведение двух множеств
- •Тема 6.4. Способы задания множеств, конечные и бесконечные множества
- •7. Основы теории вероятностей и математической статистики
- •Тема 7.1. Элементы комбинаторики
- •Тема 7.2. Классическое определение вероятности
- •Тема 7.3. Характеристики вариационного ряда Выборочное среднее
- •Тема 7.4. Математическое ожидание дискретной случайной величины
- •8. Основные численные методы
- •Тема 8.1. Приближенные числа и действия над ними
- •Тема 8.2. Понятие конечных разностей функции
- •Тема 8.3. Численное дифференцирование
- •Тема 8.4. Численное интегрирование
- •Тема 8.5. Приближенное решение обыкновенных дифференциальных уравнений
- •9. Основы теории комплексных чисел
- •Тема 9.1. Модуль и аргумент комплексного числа
- •Тема 9.2. Сопряженные комплексные числа
- •Тема 9.3. Действия над комплексными числами в алгебраической форме
- •Тема 9.4. Тригонометрическая форма комплексного числа
- •Тема 9.5. Показательная форма комплексного числа
- •Тема 9.6. Решение уравнений
- •10. Теория пределов
- •Тема 10.1. Предел функции в точке
- •Тема 10.2. Первый замечательный предел
- •Тема.10.3. Второй замечательный предел
- •Тема 10.4. Раскрытие неопределенности вида "бесконечность на бесконечность"
- •Тема 10.5. Раскрытие неопределенности вида "ноль на ноль"
- •Модуль 1. Основы линейной алгебры
- •Модуль 2. Основы дифференциального исчисления Производная сложной функции
- •Модуль 3. Определенный интеграл
- •Модуль 4. Применение производной функции
- •Модуль 5. Применение определённого интеграла
- •Модуль 6. Ряды Необходимый признак сходимости ряда
- •Модуль 7. Основы дискретной математики
- •Модуль 8. Основы теории вероятностей и математической статистики Теоремы сложения и умножения вероятностей
- •Модуль 9. Основы теории комплексных чисел Тригонометрическая форма комплексного числа
- •Показательная форма комплексного числа
- •Справочный материал
- •1.Основные значения тригонометрических функций
- •2. Таблица производных
- •3.Таблица интегралов
- •Библиография
Показательная форма комплексного числа
Пример
1.
Показательная форма комплексного числа
![]() имеет вид:
имеет вид:
а)
![]()
б)![]()
в)
![]()
г)![]()
Решение:
Для
того чтобы представить комплексное
число в показательной форме
![]() ,
необходимо найти его модуль r
и аргумент
.
Используя формулу
,
где x
–
действительная, а y
– мнимая часть комплексного числа,
можно найти модуль числа. В нашем случае
x
= 0,
у = 2.
Отсюда
получаем:
,
необходимо найти его модуль r
и аргумент
.
Используя формулу
,
где x
–
действительная, а y
– мнимая часть комплексного числа,
можно найти модуль числа. В нашем случае
x
= 0,
у = 2.
Отсюда
получаем:
![]() .
.
По
формулам
и
можно
найти аргумент
комплексного числа. Так как
![]() ,
,
![]() ,
то
,
то
![]() .
.
Подставляя
найденные значения r
и
в формулу, получим
![]() .
.
Ответ: в).
БЛОК 3. Кейс-задания
Пример 1
Скорость
гоночного автомобиля, движущегося
прямолинейно, изменяется по закону
![]()
Задание
1.1 (выберите
один вариант ответа).
Ускорение гоночного автомобиля в момент
времени
![]() равно …
равно …
Варианты ответов:
1) 46
2) 28
3) 12
4) 45
Ответ: 1).
Задание 1.2 (установите соответствие между элементами двух множеств). Скорость гоночного автомобиля на трассе контролируется четырьмя камерами через определенное время от начала движения. Установите соответствие между временем и скоростью передвижения гоночного автомобиля.
Варианты ответов:
1.
![]() а) 2
а) 2
2. б) 28
3.
![]() в) 102
в) 102
4.
![]() г) 490
г) 490
д) 253
Ответ: 1) – а); 2) – б); 3) – в); 4) – г).
Задание 1.3 (введите ответ в поле )
Время
гоночного автомобиля, при котором
ускорение
![]() ,
равно …
,
равно …
Ответ: 2.
Задание 1.4. (введите ответ в поле )
Путь, пройденный гоночным автомобилем за 5 секунд от начала движения, равен …
Ответ: 600.
Пример 2
Задание
2.1. Материальная
точка движется по прямой. Уравнение
скорости ее движения
![]() (м/с).
(м/с).
Ускорение материальной точки в момент времени t = 4 равно
5
9
12
17
Решение:
Ускорение
материальной точки вычисляется по
формуле:
![]() .
Отсюда
получаем
.
Отсюда
получаем
![]() (м/с2).
Подставив t
=
4, получим:
(м/с2).
Подставив t
=
4, получим:
![]() (м/с2)
(м/с2)
Ответ: в).
Задание 2.2. Материальная точка движется по прямой. Уравнение скорости ее движения (м/с). Путь, пройденный материальной точкой за 6 секунд от начала движения, равен…
Ввести ответ.
Решение:
Путь,
пройденный материальной точкой,
вычисляется по формуле:

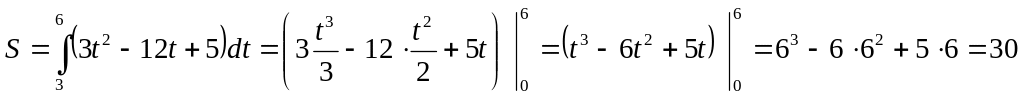
Ответ: 30 м.
Пример 3
Задание
3.1. Материальная
точка движется по прямой. Уравнение ее
движения
![]() (м/с).
Ускорение материальной точки в момент
времени t
=
5 равно …
(м/с).
Ускорение материальной точки в момент
времени t
=
5 равно …
87
22
42
30
Решение:
Ускорение материальной точки вычисляется по формуле:
![]() (м/с2)
(м/с2)
![]() (м/с2)
(м/с2)
Ответ: г).
Задание 3.2. Материальная точка движется по прямой. Уравнение скорости ее движения (м/с). Путь, пройденный материальной точкой за 3 секунды от начала движения, равен…
Ввести ответ.
Решение:
Путь, пройденный материальной точкой, вычисляется по формуле:
 (м)
(м)
Ответ: 63 м.
Задания для самостоятельного решения:
Точка движется прямолинейно по закону
 .
.
Найти скорость точки в момент времени t = 4.
Точка движется прямолинейно по закону

Найти скорость точки в момент времени t = 2.
Скорость точки, движущейся прямолинейно, задана уравнением
 .
Найти ускорение точки в момент времени
t
=
3.
.
Найти ускорение точки в момент времени
t
=
3.Скорость точки, движущейся прямолинейно, задана уравнением
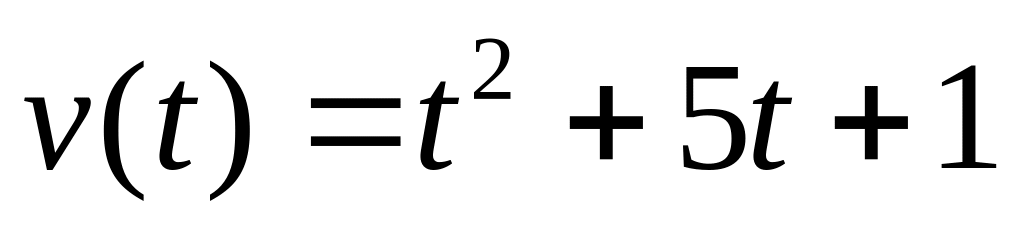 .
Найти путь, пройденный точкой за 3
секунды от начала движения.
.
Найти путь, пройденный точкой за 3
секунды от начала движения.Точка движется прямолинейно по закону
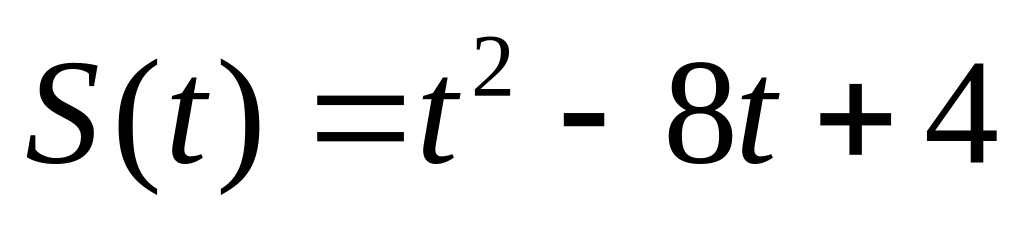 .
В какой момент времени скорость точки
окажется равной нулю?
.
В какой момент времени скорость точки
окажется равной нулю?
Ответы:
104; 2) 32; 3) 7; 4) 34,5; 5) 4.
ТЕСТ для самопроверки
Блок 1
Задание 1. (выбрать один вариант ответа)
Решить систему линейных уравнений по формулам Крамера.
![]()
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г) .
;
г) .
Задание 2. (выбрать один вариант ответа)
Производная
функции
![]() равна …
равна …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 3 (выбрать один вариант ответа)
Производная
сложной функции
![]() равна …
равна …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 4. (выбрать один вариант ответа)
Производная
функции
![]() в точке
в точке
![]() равна …
равна …
Варианты ответов:
а) 36; б) 33; в) – 28 ; г) 28.
Задание 5. (выбрать один вариант ответа)
Неопределённый
интеграл
![]() равен …
равен …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 6. (выбрать один вариант ответа)
Определённый
интеграл
![]() равен …
равен …
Варианты ответов:
а)
2; б) – 2; в) 3; г)
![]() .
.
Задание 7. (выбрать один вариант ответа)
Общим
решением дифференциального уравнения
с разделяющимися переменными
![]() является …
является …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 8. (выбрать один вариант ответа)
Общим
решением дифференциального уравнения
второго порядка
![]() является …
является …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 9. (выбрать один вариант ответа)
Частичная
сумма S3
ряда
![]() равна …
равна …
Варианты ответов:
а) 3; б) 9; в) – 9; г) 6.
Задание 10. (выбрать один вариант ответа)
Пусть
![]() ;
;
![]() .
Тогда прямое произведение
.
Тогда прямое произведение
![]() равно …
равно …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 11. (выбрать один вариант ответа)
Пусть
![]() ;
;
![]() .
Тогда
.
Тогда
![]() равно …
равно …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 12. (выбрать один вариант ответа)
В корзине 15 красных и 5 белых шаров. Наугад вынутый шар окажется красным с вероятностью равной …
Варианты ответов:
а)
0,75; б) 0,05; в)
![]() ;
г) 1.
;
г) 1.
Задание 13. (выбрать один вариант ответа)
Сколькими способами можно составить список из пяти человек?
Варианты ответов:
а) 5; б) 25; в) 100; г) 120.
Задание 14. (выбрать один вариант ответа)
При
вычислении значения выражения
![]() данные
в условии задачи значения х
= 10,2 и у
= 3,8 округлили до целых и получили
данные
в условии задачи значения х
= 10,2 и у
= 3,8 округлили до целых и получили
![]() .
Тогда абсолютная погрешность полученного
результата равна …
.
Тогда абсолютная погрешность полученного
результата равна …
Варианты ответов:
а) – 1,2; б) – 0, 2; в) 0,2; г) 1,2.
Задание 15. (выбрать один вариант ответа)
Сопряжённое
комплексное число для
![]() имеет вид …
имеет вид …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 16. (выбрать один вариант ответа)
Предел
функции
![]() равен …
равен …
Варианты ответов:
а)
2;
б) – 2; в)
![]() ;
г)
.
;
г)
.
Блок 2
Задание 17. (вычислите ответ)
Если
![]() ,
то
,
то
![]() принимает значение, равное …
принимает значение, равное …
Задание 18. (вычислите ответ)
Определённый
интеграл
![]() равен …
равен …
Задание 19. (выберите не менее двух вариантов ответа)
Частными
решениями дифференциального уравнения
![]() являются …
являются …
Варианты ответов:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() ;
г)
;
г)
![]() .
.
Задание 20
Даны
комплексные числа
![]() и
и
![]() .
Установите соответствие между действиями
над комплексными числами и результатами
этих действий.
.
Установите соответствие между действиями
над комплексными числами и результатами
этих действий.
Варианты ответов:
 а)
а)
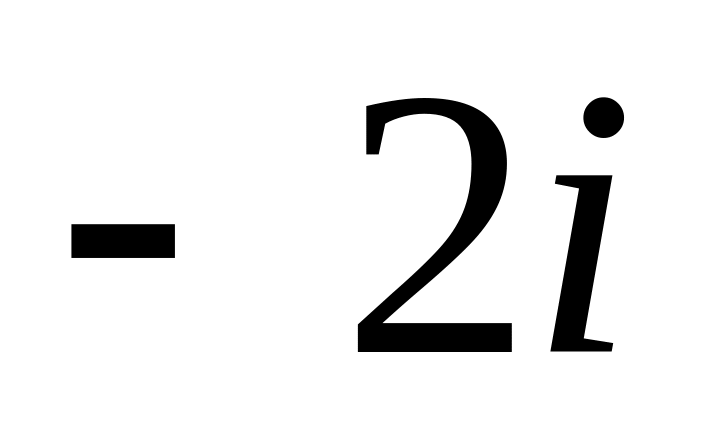
 б)
б)
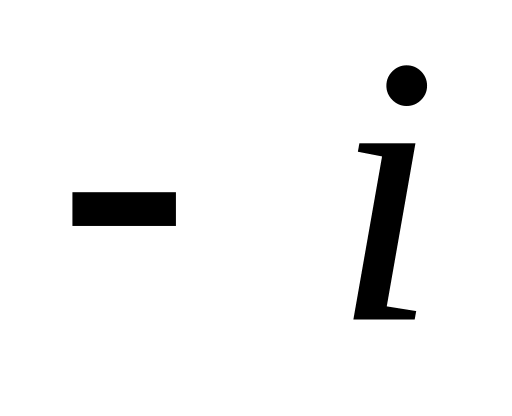
 в)
2
в)
2
Блок 3
Пример 21
Скорость
автомобиля, движущегося прямолинейно,
изменяется по закону
![]() (м/с).
(м/с).
Задание 21.1. (выбрать один вариант ответа)
Ускорение автомобиля в момент времени t = 3 сек равно …
Варианты ответов:
а) 66; б) 22; в) 30; г) 20.
Задание 21.2. (установите соответствие между элементами двух множеств)
Установите соответствие между временем и скоростью автомобиля.
Варианты ответов:
t = 1 а) 20;
t = 2 б) 64;
t = 3 в) 7;
t = 4 г) 39;
д) 70.
Задание 21.3. (вычислите ответ)
Время, при котором ускорение автомобиля а = 46 м/с2, равно …
Задание 21.4. (вычислите ответ)
Путь, пройденный автомобилем за 4 секунды от начала движения равен …
Ответы: 1. а); 2. б); 3. в); 4. г); 5. в); 6. а); 7. г); 8. г); 9. б); 10. б); 11. а); 12. а); 13. г); 14. г); 15. а); 16. в); 17. 20; 18. 63; 19. б); 20. 1) – в); 2) – а); 3) – б); 21.1. б); 21.2. 1) – б); 2) – а); 3) – г); 4) – б); 21.3. 7; 21.4. 96.
