Модуль 9. Основы теории комплексных чисел Тригонометрическая форма комплексного числа
Пример
1.
Тригонометрическая форма комплексного
числа
имеет вид …
Решение:
Для
того чтобы представить комплексное
число в тригонометрической форме записи,
необходимо найти его модуль r
и аргумент
.
Используя формулу
,
где x
–
действительная, а y
– мнимая часть комплексного числа,
можно найти модуль числа:
.
По
формулам
и
можно
найти аргумент
комплексного числа (обращаем внимание,
что под аргументом
понимается его главное значение, то
есть значение, удовлетворяющее условию
).
Так
как
,
,
то
.
Зная,
что тригонометрическая форма комплексного
числа имеет вид:
,
получим
.
Ответ: а).
Пример 2. Тригонометрическая форма комплексного числа z = 3i имеет вид…
1)
z
= 3 (
+
i
)
2)
z
= 3 (
−
i
)
3)
z = −3 (
+
i
)
4)
z = 3 (
+
i
)
Решение:
z = 3i => z = 0 + 3i – алгебраическая форма комплексного числа
z = r (cosφ + i sin φ) – тригонометрическая форма комплексного числа
r
=
=
=
= 3
M
(0;3) => М 
ОУ
=> φ =
=
z
= 3∙ (сos
+
i
)
– тригонометрическая форма комплексного
числа
Ответ: 1).
èЗадание
1.
Тригонометрическая форма комплексного
числа z
= 1+
имеет вид…
1)
z
= 2 (
)
2)
z
= 2 (
)
3)
z
= 2 (
)
4)
z
= 2 (
)
Ответ: 3)
èЗадание 2. Тригонометрическая форма комплексного числа z = 7 имеет вид…
1)
z
= 7 (
)
2) z = 7 (sin π + i cos π)
3) z = 7 (cos 0 + i sin 0)
4) z = 7 (sin 0 + i cos 0)
Ответ: 3).
èЗадание 3. Тригонометрическая форма комплексного числа z = −2 + 2i имеет вид…
1)
z
= 2 
( 
− 
)
2)
z
= 2
(
+ 
)
3)
z
= 2
(
+ 
)
4)
z
= 2
( 
)
+ 
))
Ответ: 3).
èЗадание 4. Тригонометрическая форма комплексного числа z = − 4 i имеет вид…
1)
z
= 4 (
)
2) z = 4 (cos (− ) + i sin (− ))
3)
z = 4 (sin
+
i
cos 
)
4) z = 4 (sin (− ) + i cos (− ))
Ответ: 2).
Задание
5.
Тригонометрическая форма комплексного
числа
имеет вид …
а)
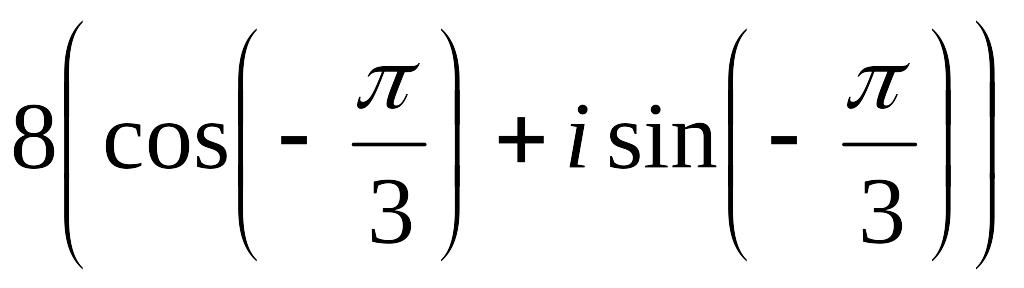
б)
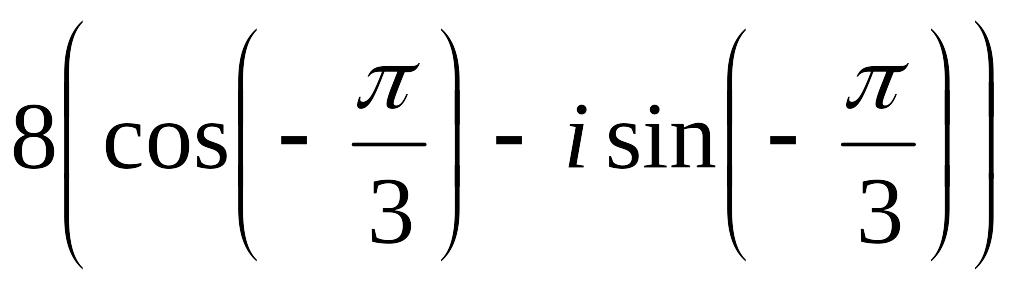
в)
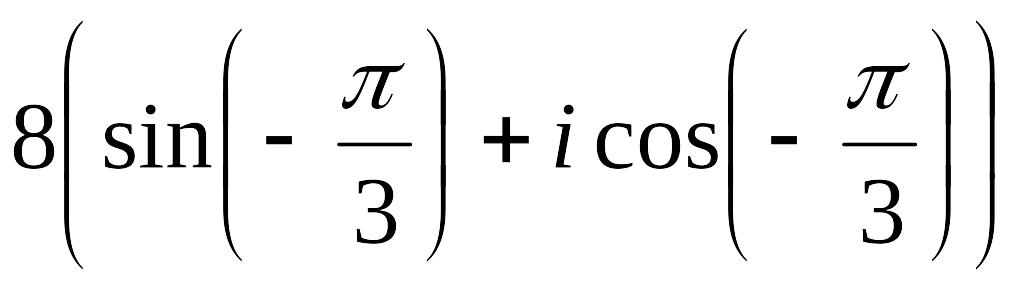
г)
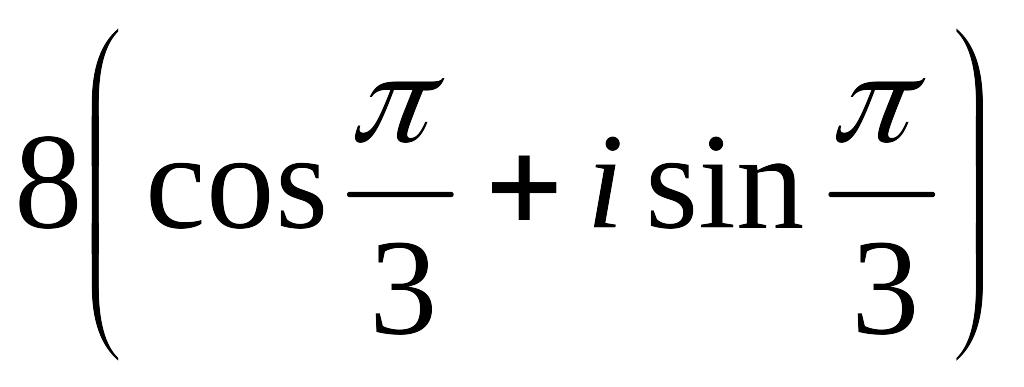
Ответ: а).
Задание
6.
Тригонометрическая форма числа
имеет
вид…
а)
б)
в)
г)
Ответ: б).
Задание
7.
Тригонометрическая форма числа
имеет
вид…
а)
б)
в)
г)
Ответ: в).
Пример
3.
Произведение комплексных чисел
и
равно …
а)
б)
в)
г)
Решение:
Воспользуемся
формулой:
.
Получим:
.
Ответ: а).
Задание
8.
Найдите
произведение
комплексных чисел в алгебраической
форме:
Ответ:
Задание
9.
Найдите частное
комплексных чисел в алгебраической
форме, если
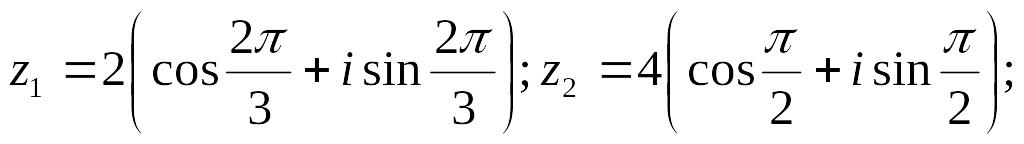
Ответ:
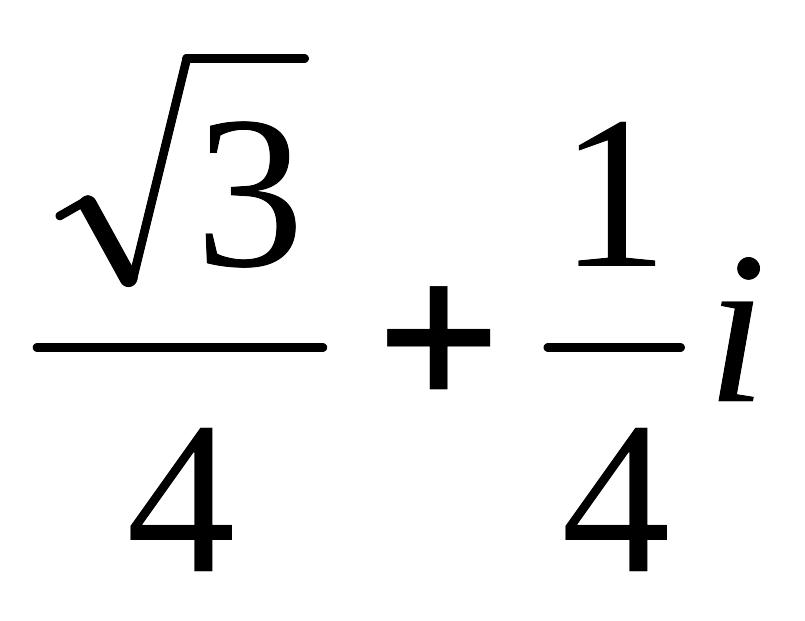
Задание
10.
Найдите произведение
комплексных чисел в тригонометрической
форме:
;
.
а)
б)
в)
г)
Ответ: а).
Задание
11.
Найдите
частное
комплексных чисел в тригонометрической
форме:
.
Ответ:
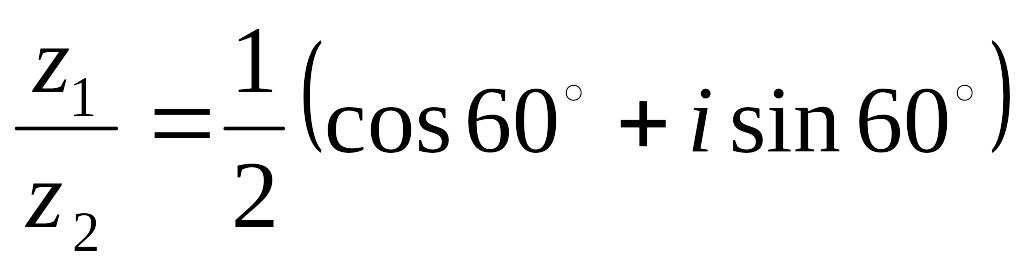
Пример
4. Дано
комплексное число
.
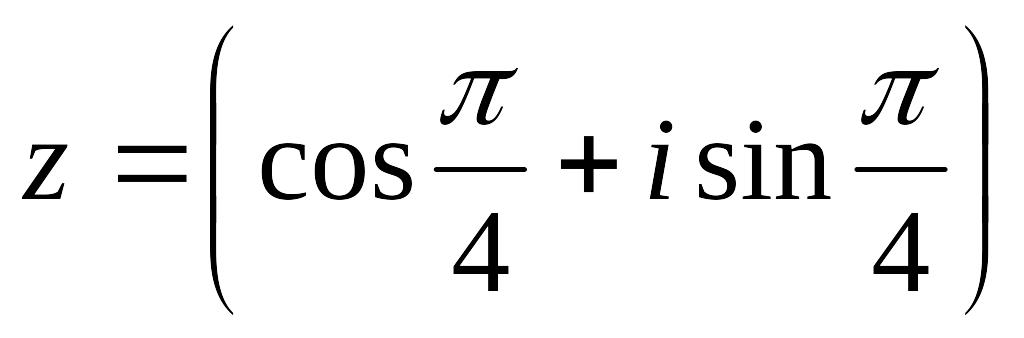Тогда значение
равно …
а)
б)
в)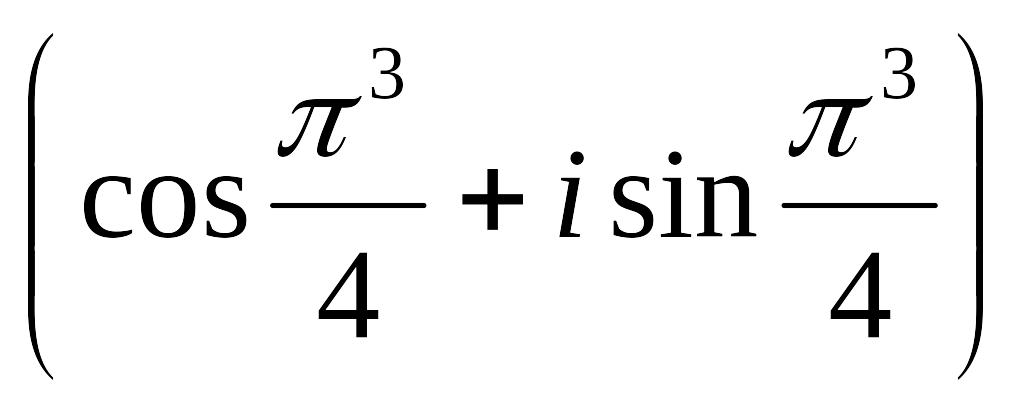
г)
Решение:
Обращаем
внимание, что в данном случае нужно
воспользоваться формулой Муавра
.
В нашем случае n
= 3,
r
= 1. Значит,
.
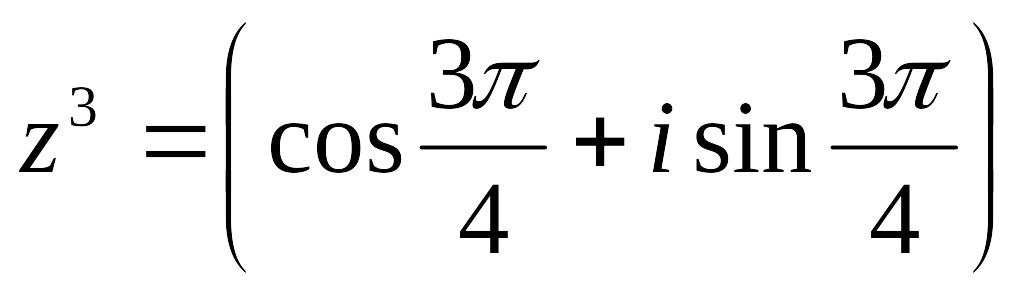Ответ: а).
Задание
12.
Возведите в степень в тригонометрической
форме:
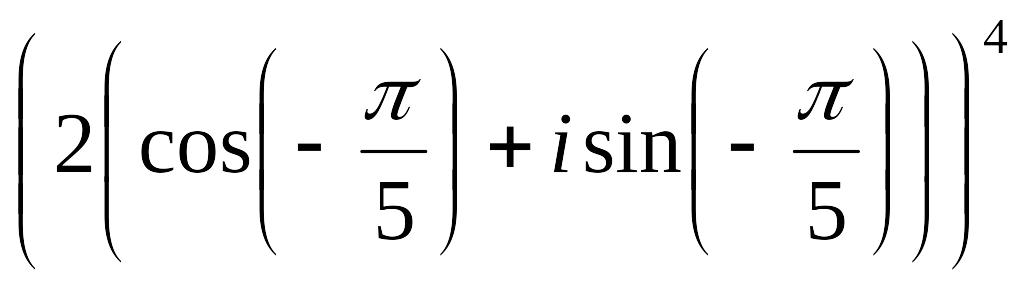
а)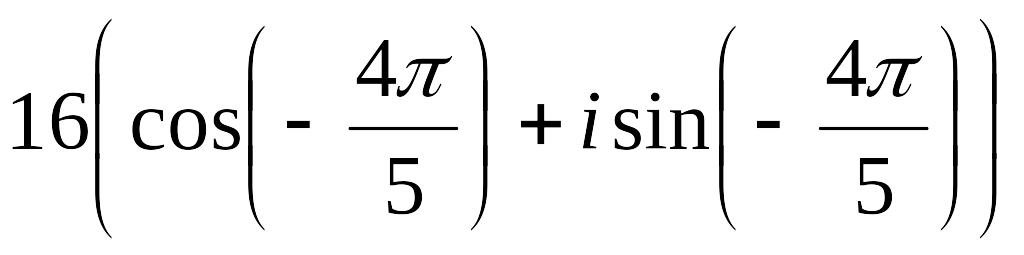
б)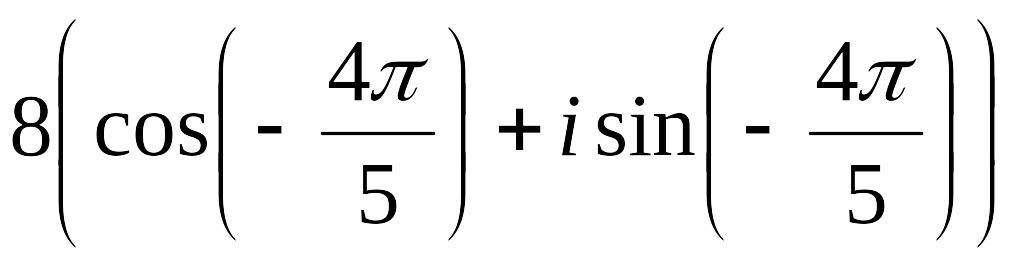
в)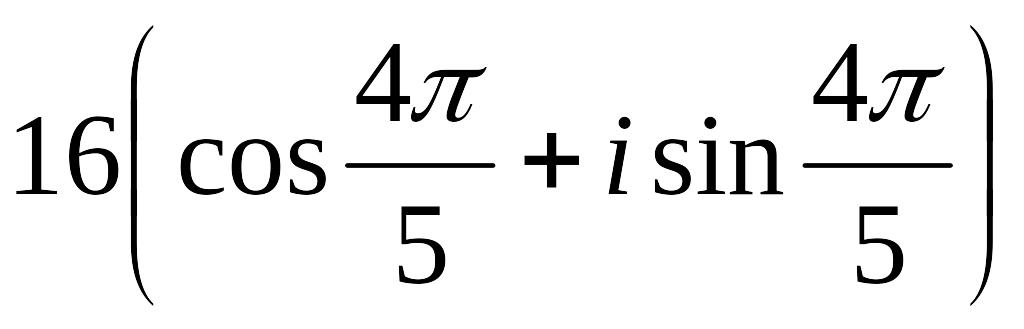
Ответ: а).
Задание
13. Возведите
в степень в тригонометрической форме:
а)
б)
в)
г)
Ответ: б).
Задание
14.
Возведите
в степень
.
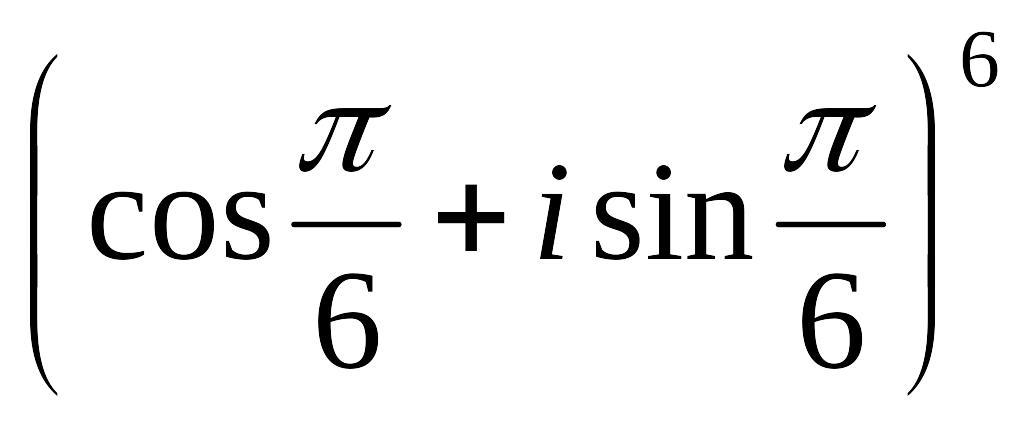Результат запишите в алгебраической
форме:
а)
б)
в)
г)
Ответ: а).