
- •Учебно-методическое пособие для подготовки к интернет-тестированию по математике
- •Содержание
- •Введение
- •Основы линейной алгебры
- •Тема 1.1. Действия над матрицами
- •Тема 1.2. Определители второго порядка
- •Тема 1.3. Системы линейных уравнений
- •2. Дифференциальное исчисление
- •Тема 2.1. Правила дифференцирования
- •Тема 2.2. Производная сложной функции
- •Тема 2.3. Производная функции в точке
- •Тема 2.4. Экстремум функции
- •Тема 2.5. Наибольшее и наименьшее значения функции на отрезке
- •3. Интегральное исчисление
- •Тема 3.1. Неопределенный интеграл
- •Тема 3.2. Методы вычисления неопределенных интегралов
- •Тема 3.3. Определенный интеграл
- •Тема 3. 4. Свойства определенного интеграла
- •Тема 3.5. Геометрические приложения определенного интеграла
- •4. Дифференциальные уравнения
- •Тема 4.1. Основные понятия теории дифференциальных уравнений
- •Тема 4.2. Дифференциальные уравнения первого порядка с разделяющимися переменными
- •Тема 4.3. Линейные дифференциальные уравнения первого порядка
- •Тема 4.4. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •5. Ряды
- •Тема 5.1. Числовые ряды
- •Тема 5.2. Сумма числового ряда
- •Тема 5.3. Степенные ряды
- •6. Основы дискретной математики
- •Тема 6.1. Числовые множества. Основные понятия теории множеств
- •Тема 6.2. Действия над множествами
- •Тема 6.3. Прямое произведение двух множеств
- •Тема 6.4. Способы задания множеств, конечные и бесконечные множества
- •7. Основы теории вероятностей и математической статистики
- •Тема 7.1. Элементы комбинаторики
- •Тема 7.2. Классическое определение вероятности
- •Тема 7.3. Характеристики вариационного ряда Выборочное среднее
- •Тема 7.4. Математическое ожидание дискретной случайной величины
- •8. Основные численные методы
- •Тема 8.1. Приближенные числа и действия над ними
- •Тема 8.2. Понятие конечных разностей функции
- •Тема 8.3. Численное дифференцирование
- •Тема 8.4. Численное интегрирование
- •Тема 8.5. Приближенное решение обыкновенных дифференциальных уравнений
- •9. Основы теории комплексных чисел
- •Тема 9.1. Модуль и аргумент комплексного числа
- •Тема 9.2. Сопряженные комплексные числа
- •Тема 9.3. Действия над комплексными числами в алгебраической форме
- •Тема 9.4. Тригонометрическая форма комплексного числа
- •Тема 9.5. Показательная форма комплексного числа
- •Тема 9.6. Решение уравнений
- •10. Теория пределов
- •Тема 10.1. Предел функции в точке
- •Тема 10.2. Первый замечательный предел
- •Тема.10.3. Второй замечательный предел
- •Тема 10.4. Раскрытие неопределенности вида "бесконечность на бесконечность"
- •Тема 10.5. Раскрытие неопределенности вида "ноль на ноль"
- •Модуль 1. Основы линейной алгебры
- •Модуль 2. Основы дифференциального исчисления Производная сложной функции
- •Модуль 3. Определенный интеграл
- •Модуль 4. Применение производной функции
- •Модуль 5. Применение определённого интеграла
- •Модуль 6. Ряды Необходимый признак сходимости ряда
- •Модуль 7. Основы дискретной математики
- •Модуль 8. Основы теории вероятностей и математической статистики Теоремы сложения и умножения вероятностей
- •Модуль 9. Основы теории комплексных чисел Тригонометрическая форма комплексного числа
- •Показательная форма комплексного числа
- •Справочный материал
- •1.Основные значения тригонометрических функций
- •2. Таблица производных
- •3.Таблица интегралов
- •Библиография
9. Основы теории комплексных чисел
Тема 9.1. Модуль и аргумент комплексного числа
Комплексными
числами
называют выражения вида
![]() ,
где х
и y
– действительные числа, а
,
где х
и y
– действительные числа, а
![]() –
мнимая единица. Всякое комплексное
число
может быть изображено на плоскости
точкой с координатами (х;у)
и соответствующим вектором (см.
рис. 5).
–
мнимая единица. Всякое комплексное
число
может быть изображено на плоскости
точкой с координатами (х;у)
и соответствующим вектором (см.
рис. 5).
М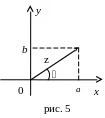 одулем
комплексного
числа называется длина вектора,
соответствующего этому числу.
одулем
комплексного
числа называется длина вектора,
соответствующего этому числу.
Модуль комплексного числа вычисляется по формуле:
r
=![]() .
.
Аргументом комплексного числа называется величина угла между положительным направлением действительной оси и вектором, соответствующим этому числу. Обозначение: arg z = .
Пример
1. Найдите
модуль комплексного числа
![]() .
.
Решение:
Модуль
комплексного числа вычисляется по
формуле
,
где x
–
действительная, а y
– мнимая часть комплексного числа.
Тогда
![]() .
.
Ответ:
![]() .
.
Задание 1. Изобразите комплексные числа на плоскости:
Задание 2. Найдите модуль комплексного числа:
Ответы:
1) 10; 2) 5; 3) 2; 4) 1; 5) 1; 6)
![]() ;
7)
;
7)
![]() .
.
Задание
3.
Модуль
числа
![]() равен …
равен …
1) 12 3) 5
2) 13 4) 4
Ответ: 2) 13.
Тема 9.2. Сопряженные комплексные числа
Комплексно
сопряжёнными числами
называют числа
и
![]() .
Например,
.
Например,
![]() и
и
![]() .
.
Пример 1. Даны четыре комплексных числа:
1)
![]()
2)
![]()
3)
![]()
4)
![]()
Установите соответствие между комплексными числами и им сопряженными.
Ответ: 1) – b); 2 – a); 3) – e); 4) – c).
Задание Запишите комплексно сопряженное число:
Ответы:
1).
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() ;
4)
;
4)
![]() ;
5)
;
5)
![]() ;
;
6)
![]() ;
7)
;
7)
![]() ;
8)
;
8)
![]() ;
9)
;
9)![]() ;
10)
;
10)
![]() .
.
Тема 9.3. Действия над комплексными числами в алгебраической форме
Пример
1.
Произведение комплексных чисел
![]() и
и
![]() равно …
равно …
Решение:
![]()
Ответ: 85.
Задание
1.
Установите соответствие между действиями
над комплексными числами
![]() ;
;
![]() и результатами действий:
и результатами действий:
 a)
a)
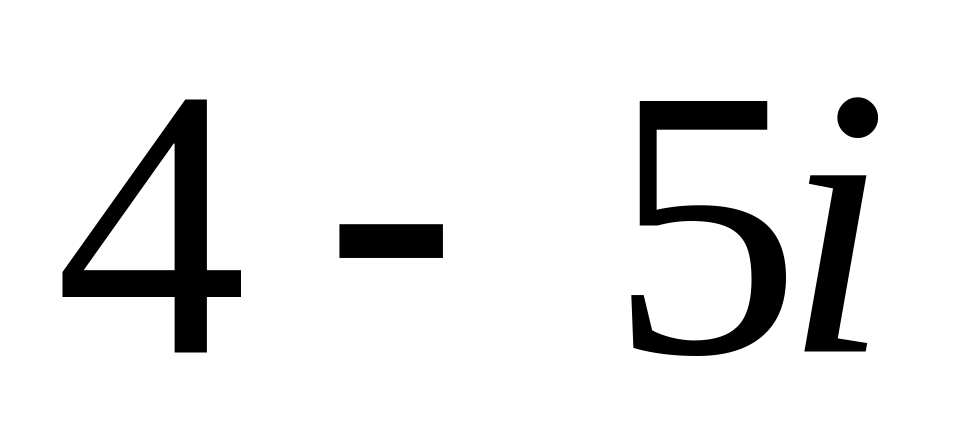
 b)
b)

 c)
c)

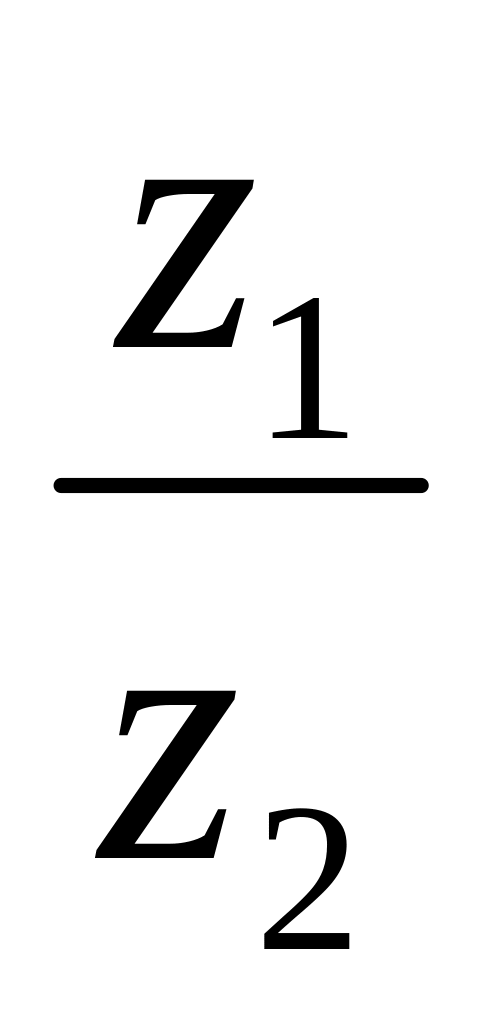 d)
d)
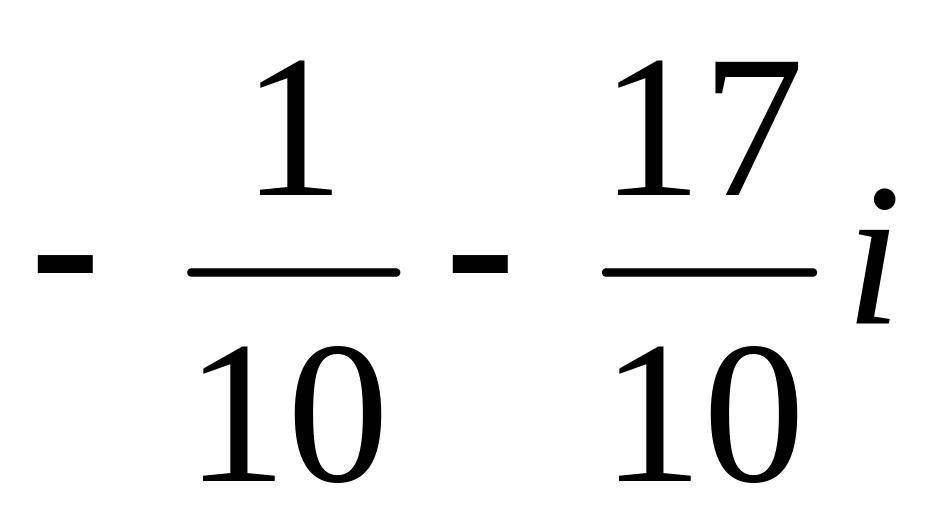
Ответ: 1) – с); 2) – а); 3) – b); 4) – d).
Задание 2. Выполните действия над комплексными числами в алгебраической форме:
 =
= =
= =
= =
=
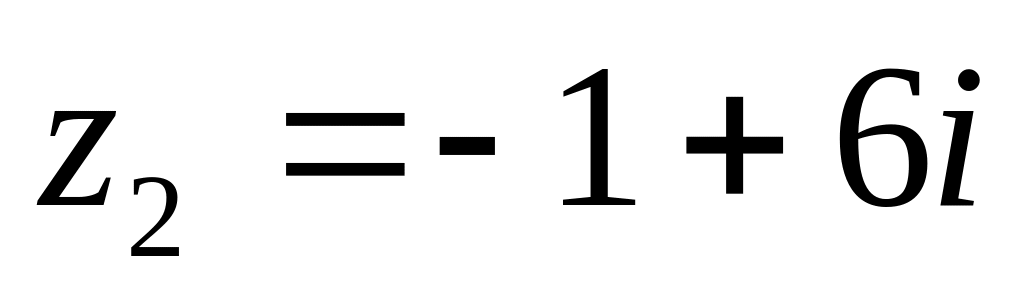 ;
;






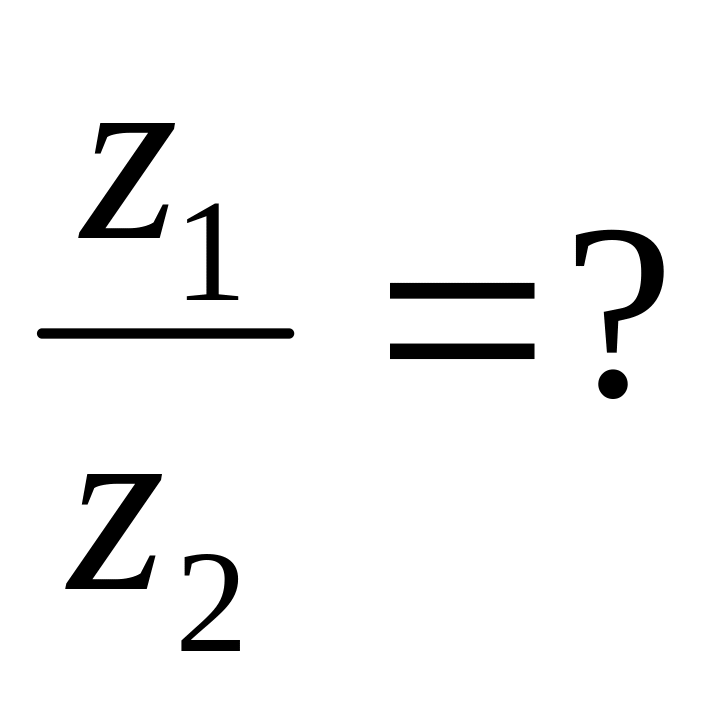

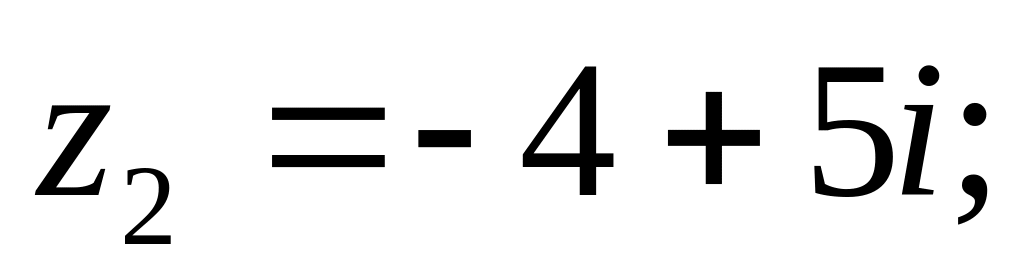
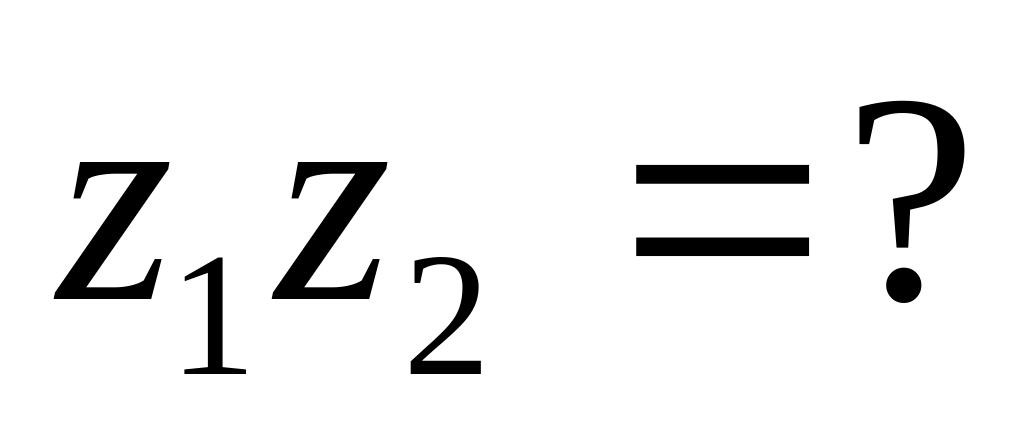
 =
=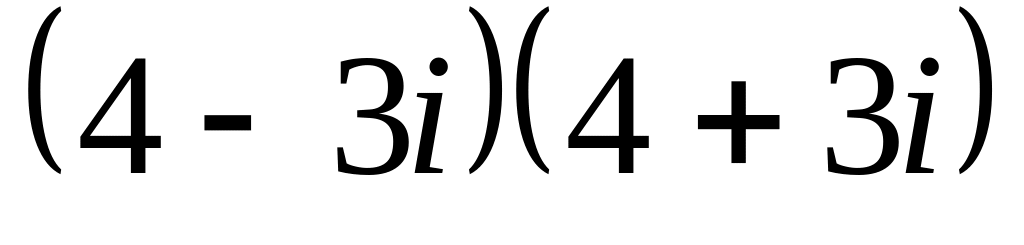 =
=
Ответы:
1) 1; 2)
![]() 3)
3)
![]() 4)
4)
![]() 5)
5)
![]() 6)
6)
![]() 7)
7)
![]()
8)
![]() 9) 20; 10) 25.
9) 20; 10) 25.
Тема 9.4. Тригонометрическая форма комплексного числа
Запись
комплексного числа в виде
![]() ,
где r
– модуль,
а
– аргумент
комплексного числа, называется
тригонометрической формой комплексного
числа.
,
где r
– модуль,
а
– аргумент
комплексного числа, называется
тригонометрической формой комплексного
числа.
Задание
1.
Модуль числа
![]() равен …
равен …
Ответ: 3.
Задание 2. Тригонометрическая форма комплексного числа, имеющего модуль r = 4 и аргумент = 210° имеет вид:
а)
![]()
б)
![]()
в)
![]()
г)![]()
Ответ: б).
Задание
3.
Тригонометрическая форма числа
![]() имеет вид:
имеет вид:
а)
![]()
б)![]()
в)
![]()
г)![]()
Ответ: в).
Задание 4. Запишите комплексное число в тригонометрической форме
а)![]()
б)![]()
в)![]()
г)![]()
Ответ: б).
