Тема12. Формирователи и генераторы импульсных сигналов

Ранее были рассмотрены генераторы импульсных сигналов на базе ОУ и RC-цепей (релаксационные генераторы), схемы аналогичного назначения могут быть также реализованы на логических элементах и RC- цепях. В импульсной технике применяются RC-цепи нескольких разновидностей, ниже рассмотрены основные из них. Практически наиболее часто применяются цепи первого порядка, т.е. с одной реактивностью (обычно одним конденсатором) и при воздействии на входе прямоугольного импульса, кроме того предполагается, что цепь является линейной (параметры составляющих цепь элементов неизменны в реальном диапазоне изменения токов и напряжений). Целью анализа таких цепей является определение реакции цепи на её выходе в переходном процессе. При указанных условиях применим классический метод анализа, как наиболее простой, суть его сводится к анализу решения дифференциального уравнения, описывающего поведение RC-цепи. Для анализа цепей более высоких порядков применяется операторный метод, для входных воздействий в виде импульсов сложной формы (пилообразных, трапецеидальных и пр.) применяется метод интеграла свёртки (Дюамеля) , для импульсных сигналов с высокочастотным заполнением (радиоимпульсов) применяется метод спектрального анализа. Далее рассматривается подробно классический метод, как наиболее часто используемый на практике. На рис.113 приведена RC-цепь на входе которой действует прямоугольный импульс с параметрами , указанными на рисунке, выходными величинами являются напряжения на резисторе Ur и на конденсаторе Uс.

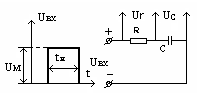
Рис.113

Линейная RC - цепь

Переходный процесс в такой цепи описывается дифференциальным неоднородным уравнением первого порядка (аналогичным с рассмотренным выше для заряда в базе транзистора, но с другими переменными).Так для напряжения на конденсаторе имеем:

t* dUс/dt + Uс = Uм и решение: Uс(t) = Uс() - [ Uс (¥) – Uс (0) ]*е^-t/t ,

здесь граничные условия: Uс(¥) = Uм (напряжение, до которого зарядился бы конденсатор при tи = ¥), Uс (0) = 0 (напряжение в момент поступления переднего фронта входного импульса) , = RC – постоянная времени цепи.

Для временного интервала , в котором напряжение на конденсаторе изменится с Uс(t1) до Uс(t2) из общего решения можно получить:

Dt = t2 – t1 =t*ln{Uс(¥)-Uс(t1)}/ { Uс(¥) - Uс(t2)}

Для напряжения на резисторе Ur приведенные соотношения, с учётом замены переменной имеют аналогичную структуру:

t* dUr /dt + Ur = Uм , Ur (t) = Ur (¥) - [ Ur (¥) – Ur (0) ]*е^-t/t ,

Dt = t2 – t1 = =t*ln{Ur (¥)-Ur (t1)}/ {Ur(¥) - Ur (t2)} ,

здесь Ur (t1) и Ur (t2) – напряжения на резисторе в начальный (t1) и конечный (t2) моменты времени соответственно.

В зависимости от соотношения длительности входного импульса и постоянной времени RC-цепи переходные процессы имеют характерные особенности, отражаемые в их названии, ниже приведены основные разновидности RC-цепей по указанному признаку.

Если выходным является напряжение на конденсаторе, то практический интерес представляют два случая:

• tи« t , цепь носит название интегрирующей, из-за большой постоянной времени конденсатор в течение tи успевает зарядиться до небольшого напряжения, причём напряжение на нём возрастает практически линейно (начальный участок экспоненты), временная диаграмма приведена на рис.114.

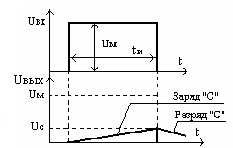
Рис. 114

Реакция интегрирующей цепи на

прямоугольный входной импульс

В идеальном случае должно выполняться соотношение:

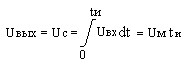
Р еально найти величину Uвых можно следующим образом: по второму закону Кирхгофа Uм = Ur + Uс ,поскольку Uс « Ur, можно считать: Uм ≈ Ur, ток через конденсатор равен : Iс =C* dUc/dt и является общим для цепи, следовательно, можно считать, что:

Поскольку начальный участок экспоненты (заряд конденсатора) не является идеальной прямой линией, то и «качество» интегрирования не идеально, оно оценивается относительным изменением производной функции заряда конденсатора в начале и конце входного импульса (). Из общего решения дифференциального уравнения, приведенного выше , при граничных условиях Uс (0) = 0 и Uс (¥) = Uм найдем :

Uс = Uм - [ Uм –0 ]*е^-t/t = Uм*(1 - е^-t/t), тогда:

b = (dUc/dt_t=0 - dUc/dt|_t=tи)/(dUc/dt|_t=0) =1 - е^-tи/t ≈tи/ (из разложения в ряд функции e^x =

1 + х +…).

Таким образом, видно, что чем лучше выполняется неравенство tи « t тем выше качество интегрирования (меньше коэффициент , для линейной зависимости b =0). Следует отметить, что интегрирующая цепь является основой построения формирователей и генераторов линейно изменяющегося напряжения. В этом случае часто необходимо обеспечить быстрый разряд конденсатора после окончания входного импульса. Один из способов показан на рис.115, временные диаграммы приведены на рис.116 малая постоянная времени цепи разряда конденсатора обеспечивается небольшим сопротивлением прямо смещённого p-n перехода , шунтирующего резистор цепи диода.

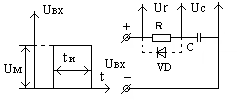
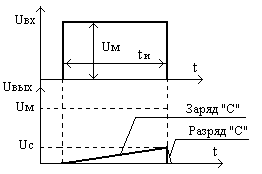
Рис.115 Рис.116

Интегрирующая цепь с диодом Временные диаграммы интегрирующей

цепи с диодом

• tи » t , RC-цепь при таком соотношении постоянной времени и длительности входного импульса практически не искажает фронты выходного импульса, т.к. время заряда конденсатора мало. Временные диаграммы неискажающей цепи приведены на рис.117.

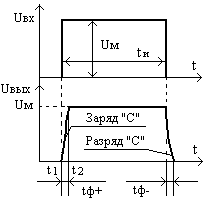
Рис.117

Временные диаграммы RC-цепи

при tи » t

Оценку длительности фронтов можно произвести по приведенной выше общей формуле для промежутка времени для RC-цепи, обычно полагают, что формирование фронта закончено при достижении напряжения на конденсаторе 95% максимально возможного значения. Тогда в данном случае граничные условия будут выглядеть следующим образом:

Uс(¥) = Uм, Uс (0) = Uс (t1)=0, Uс (t2) = 0,95 Uм, далее получим:

tф+ = t2 – t1 =t*ln(Uм - 0)/ (Uм – 0,95 Uм) = t*ln20 = 3 t Поскольку постоянные времени заряда и разряда конденсатора в данном случае одинаковы, то tф+ = tф-.

Если выходным является напряжение на резисторе, то практический интерес представляют также два случая:

• tи« t, цепь носит название разделительной , из-за большой постоянной времени конденсатор в течение tи успевает зарядиться до небольшого напряжения , тогда на резисторе в первый момент выделяется максимальное значение напряжения входного импульса (первый закон коммутации). Далее напряжение на резисторе в течение длительности входного импульса уменьшается практически линейно (начальный участок экспоненты заряда конденсатора) на величину Uc.

Если на входе цепи действует последовательность однополярных, например, положительных импульсов, то конденсатор разделяет постоянную и переменную составляющие напряжения этой последовательности и на резисторе выделяется только переменная составляющая. Качественно процессы в цепи для указанного соотношения tи « t поясняются временной диаграммой на рис.118.

Рис.118

Реакция разделительной цепи

на входную последователь-

импульсных сигналов

По окончании первого импульса последовательности напряжение на резисторе меняет знак (U’r) и начинает нарастать, стремясь к нулю во время действия паузы tп, поскольку конденсатор разряжается через резистор и внутреннее сопротивление источника входного сигнала. Из-за разных граничных условий для фаз заряда и разряда конденсатора (при заряде напряжение на конденсаторе стремится к высокому значению Uм, а при разряде небольшое напряжение U’с стремится к нулю) отрицательное напряжение на резисторе в течение паузы tп изменяется незначительно, т.е. U’r≈U’’r. Второй импульс входной последовательности скачкообразно изменит полярность напряжения на резисторе, однако теперь напряжение на нём будет меньше максимального (Uм) на величину D U’’с, т.е. импульсная последовательность на выходе цепи сдвигается вниз относительно оси абсцисс. После нескольких входных импульсов ( их число зависит от параметров конкретной цепи) установится стационарный процесс, характеризующийся отсутствием постоянной составляющей Uср и равенством площадей положительного и отрицательного импульсов (S1=S2). Указанное равенство объясняется тем, что при отсутствии постоянной составляющей напряжения (и тока) на конденсаторе, его заряд усреднённый за период будет равен нулю, т.е. происходит обмен энергией между источником входного сигнала и конденсатором (заряд, накопленный конденсатором в течение импульса, возвращается в источник входного сигнала во время паузы). Площадь импульса S =U*t =R*I*t= R*Q, где Q=I*t – заряд конденсатора, пропорциональна заряду, следовательно. в установившемся процессе S1=S2.

Как видно из временной диаграммы, разделительная цепь вносит искажения в форму выходных импульсов, характеризуемые коэффициентом относительного завала вершины, который в общем виде определяется по формуле:  = Ur/(0,5Uм) , поскольку Ur = Uс = Uм*(1 - е^-t/t), то при граничных условиях для данного случая: Uс(¥) =0,5 Uм, Uс (0) = 0 и пользуясь разложением экспоненциальной функции в ряд для t =tи «, как это было показано выше, получим : DUr = DUс≈ 0,5Uм*tи/ и g ≈tи/ . Таким образом, качество передачи формы импульса в разделительной цепи оценивается так же как и качество интегрирования в интегрирующей цепи и форма импульсов выходной последовательности тем лучше (ближе к прямоугольной), чем лучше выполняется соотношение tи«.

• tи » t, цепь называется дифференцирующей , действительно при ограничении: Uвых = Ur « Uвх, можно считать, что Uвх ≈ Uс, тогда Uвых ≈ I_с*R = RC* dUc/dt = RC*dUвх/dt. Качественно процесс дифференцирования показан на временных диаграммах рис. 119.

Рис.119

Реакция дифференцирующей RC –цепи на

прямоугольный входной импульс напряжения

Для идеального входного импульса производные от фронтов с нулевой длительностью описываются так называемой дельта - функцией, равной бесконечности в нулевой момент времени и нулю в остальных точках , из рисунка видно, что реальные выходные импульсы тем ближе по форме к дельта - функции , чем лучше выполняется соотношение tи » t. На спаде напряжения входного импульса ( на срезе импульса) производная меняет знак (-Uм),

физически это объясняется тем, что полярность напряжения на резисторе изменяется на противоположную в результате разряда конденсатора по цепи: резистор - внутреннее сопротивление источника входного сигнала.

Широко используются в импульсной технике линии задержки на основе рассмотренных RC – цепей и логических элементов, назначением таких цепей является формирование временного интервала заданной длительности между передними фронтами входного и выходного импульсов. Принцип работы линий задержки основан на сравнении изменяющегося напряжения на резисторе или конденсаторе с пороговым напряжением срабатывания логического элемента (ЛЭ), в момент их равенства на выходе ЛЭ формируется передний фронт выходного импульса, задержанный относительно переднего фронта входного импульса.

На рис.120 приведены схема линии задержки на основе интегрирующей цепи и временные диаграммы её работы, в качестве логического элемента (ЛЭ) может быть использован базовый элемент серий ИС - ТТЛ или КМОП (на рисунке элемент 2ИЛИ).

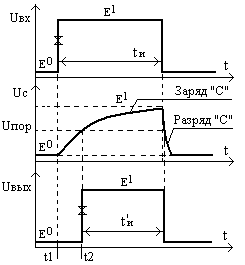
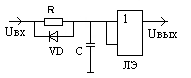
Рис.120

Линия задержки на интегрирующей

RC- цепи и временные диаграммы её

работы

Задержку можно найти по приведенной выше формуле для интервала времени, в течение которого напряжение на конденсаторе нарастало до порога срабатывания логического элемента, пользуясь при этом граничными условиями, приведенными на рисунке (фронты импульсов между которыми определяется временная задержка помечены символом «х»):

tзад = t2 – t1 = t*ln{Uс(¥)-Uс(t1)}/ { Uс(¥) - Uс(t2)} =t*ln (Е¹-Е⁰}/(Е¹ - Uпор),

здесь t = RC – постоянная времени цепи. В отличие от простой интегрирующей цепи в данном случае на условие (tи « t) –наклады -вается ограничение «сверху», действительно для того, чтобы конденсатор в течение «tи» успел зарядиться до порога срабатывания ЛЭ, должно выполняться соотношение:

Uс = Uпор = Uм (1 –­ e^-t/), где t = tи, отсюда найдём: t_макс = - tи / ln(1 – Uпор/Uм). Пользуясь приведенными выше параметрами ИС различных серий, легко показать, что: для ТТЛ t_макс  2,8 tи, для КМОП t_макс £ 1,4 tи. Время восстановления схемы к исходному состоянию после окончания входного импульса (время разряда конденсатора до уровня Е⁰) равно: tвосст. = 3*t_раз. = 3*(Rд.пр.+ Ri.ист), где Rд.пр. – сопротивление смещенного в

прямом направлении диода и Ri.ист. – внутренне сопротивление источника входного сигнала, tвосст.« tзад, т.к. (Rд.пр.+ Ri.ист) «R.

Линия задержки на дифференцирующей RC – цепи и логическом элементе 2ИЛИ-НЕ и временные диаграммы её работы показаны на рис.121. Диод, ускоряющий разряд конденсатора после окончания входного импульса, показан пунктиром, т.к. в современных сериях ИС он как правило интегрирован в кристалл микросхемы. Время восстановления схемы после окончания входного импульса можно определить аналогичным предыдущему способом. Для времени задержки с учётом замены переменных и граничных условий получим:

tзад = t2 – t1 = t*ln{Ur(¥)-Ur(t1)}/ { Ur(¥) - Ur(t2)} =t*ln (Е⁰ - Е¹) / ( Е⁰ - Uпор),

здесь t = RC – постоянная времени цепи. Максимально допустимая величина постоянной времени в данном случае (напряжение на резисторе успевает достигнуть Uпор за время tи) определяется по методике для предыду- щей линии задержки:

Ur = Uпор = Uм*e^-t/t, где t = tи, отсюда найдём: t_макс = - tи / ln(Uпор/Uм). Пользуясь приведенными выше параметрами ИС различных серий, легко показать, что: для ТТЛ t_макс £ 1,14* tи, для КМОП t_макс £ 0,69* tи.

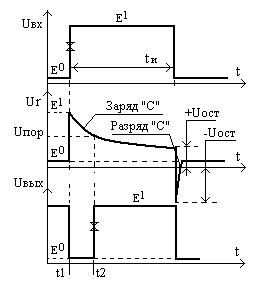
Рис.121

Схема и временные диаграммы работы линии задержки на дифференцирующей

RC-цепи и логическом элементе

Остаточные напряжения на резисторе в момент окончания входного импульса равны: + Uост = Е¹ – Uс и –Uост = Uс, где Uс = Е¹ (1- е^-tи/t).

На базе линий задержки реализуются схемы формирователей одиночных импульсов (одновибраторы или ждущие мультивибраторы) и импульсных последовательностей (релаксационные генераторы или мультивибраторы). Ниже приведены примеры таких схем.

Ждущий мультивибратор на дифференцирующей RC- цепи и логических элементах предназначен для формирования на выходе импульса заданной длительности при поступлении на вход короткого запускающего импульса. Отличительной особенностью одновибратора по сравнению с дифференцирующей цепью является наличие цепи обратной связи, удерживающей схему в квазиустойчивом состоянии на время формирования выходного импульса. При отсутствии запускающего импульса схема находится в устойчивом состоянии. Схема одновибратора на логических элементах 2И-НЕ и временные диаграммы , поясняющие его работу приведены на рис.122 и 123 соответственно.

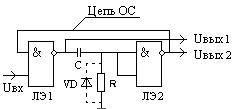
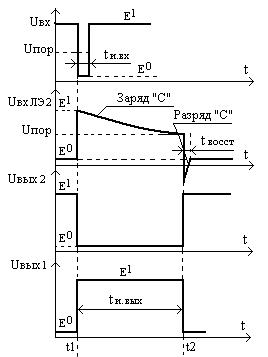
Рис.122

Схема одновибратора

Рис.123

Временные диаграммы работы одновибратора на дифференцирующей

RC-цепи и логических элементах

2И - НЕ

В исходном состоянии (устойчивом) напряжение на резисторе соответствует логическому нулю, на выходе логического элемента ЛЭ2 напряжение высокого уровня (Е¹), которое по цепи обратной связи поступает также на вход логического элемента ЛЭ1.На втором входе ЛЭ1 присутствует высокий уровень входного сигнала (Е¹) и , следовательно, на выходе ЛЭ1 в результате инверсии напряжение низкого уровня (Е⁰), конденсатор разряжен. Подача на вход одновибратора короткого входного импульса низкого уровня приводит к появлению на выходе ЛЭ1 напряжения высокого уровня, которое в первый момент целиком поступает на вход ЛЭ2 (первый закон коммутации). ЛЭ2 по выходу скачкообразно переходит в состояние логического нуля (момент времени t1) и теперь высокий уровень напряжения на выходе ЛЭ1 поддерживается уже цепью обратной связи, поскольку входной импульс закончился. Таким образом, с момента времени t1 одновибратор переходит в квазиустойчивое состояние, длительность которого определяется временем заряда конденсатора до напряжения Uс = Е¹ – Uпор по цепи: выход ЛЭ1 ‑ С - R - общая точка. Соответственно напряжение на входе ЛЭ2 уменьшается с Е¹ до Uпор (второй закон Кирхгофа) и в момент времени t2 схема возвращается в исходное устойчивое состояние, конденсатор разряжается по цепи: С - выход ЛЭ1 - общая точка - VD (диод может быть встроен в кристалл ИС).­ Длительность выходного импульса tи.вых = t2 - t1 находится по формуле, аналогичной для времени задержки дифференцирующей цепи, приведенной выше, ограничений по величине  в данном случае нет, поскольку длительность выходного импульса задаётся при проектировании схемы одновибратора с учетом частоты входных импульсов. Существенным является требование к величине времени восстановления схемы в исходное состояние, т.к. оно определяет максимально возможную частоту входных импульсов. Аналогично рассмотренным выше линиям задержки этот параметр можно определить следующим образом:

tвосст. = 3*t_раз. = 3*С*(Rд.пр.+ Rвых.ЛЭ1),

где Rд.пр. – сопротивление смещенного в прямом направлении диода и Rвых.ЛЭ1 – выходное сопротивление ЛЭ1 в состоянии логического нуля, tвосст.« tи.вых, т.к. (Rд.пр.+ Rвых.ЛЭ1) «R.

Определённые требования предъявляются к параметрам входного импульса: его длительность ( tи.вх ) должна быть по крайней мере равна или больше времени задержки срабатывания логического элемента применяемой серии ИС, кроме того, очевидно, что минимальный уровень напряжения входного импульса должен быть ниже порогового уровня срабатывания логического элемента. Уравнения для остаточных напряжений на резисторе R

(входе ЛЭ2) в момент t2 аналогичны приведенным выше для линии задержки на дифференцирующей RC- цепи.

Следует отметить, что существует достаточно много схемных реализаций одновибраторов, отличающихся типом и количеством логических элементов, однако , принцип их работы остаётся неизменным. Рассмотренная схема аппаратно более сложная, но и более универсальная, поскольку имеет как прямой так и инверсный выходы. На рис.124 приведена в качестве примера более простая схема на одном логическом элементе 2ИЛИ, имеющая один прямой выход. Как видно из временных диграмм отличие от предыдущей схемы заключается только в полярности входного импульса. В остальном временные диаграммы и расчётные соотношения аналогичны рассмотренным.

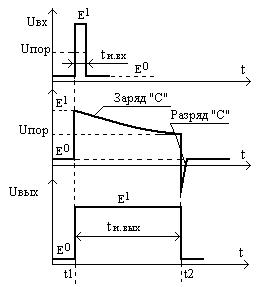
Рис.124

Одновибратор на одном ЛЭ и

временные диаграммы его работы

Мультивибратор на дифференцирующей RC - цепи и логических элементах предназначен для формирования на выходе непрерывной последовательности импульсов заданной длительности и частоты. Отличительной особенностью мультивибратора по сравнению с одновибратором является отсутствие устойчивого состояния, мультивибратор может находиться поочерёдно в двух квазиустойчивых состояниях, во время одного из них формируется длительность выходного импульса, во время другого - пауза между выходными импульсами. Существует несколько схемных реализаций мультивибраторов, однако, принцип их работы практически одинаков. Ниже рассмотрена схема на двух логических элементах и двух дифференцирующих цепях как наиболее универсальная, позволяющая генерировать импульсные последовательности с разной скважностью в широких пределах как при использовании логических элементов серии ТТЛ так и КМОП. Схема и временные диаграммы приведены на рис.125.

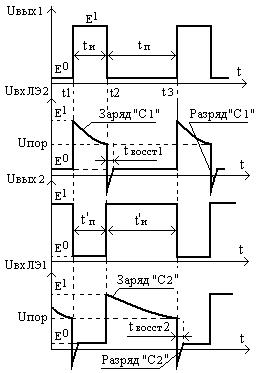
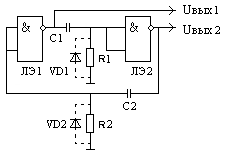
Рис.125

Схема мультивибратора на двух

логических элементах и временные

диаграммы её работы

Условно примем за начало первого квазиустойчивого состояния момент времени t1 – на прямом выходе скачкообразно появляется высокий уровень напряжения Uвых1 = Е¹, который через конденсатор С1 передаётся на вход ЛЭ2, последний переходит скачком в состояние Uвых2 = Е⁰. Это состояние сохраняется до момента t2, когда напряжение на входе ЛЭ за счёт заряда С1 не снизится до порога срабатывания ЛЭ2, таким образом формируется длительность импульса на прямом выходе (Uвых1), которую можно найти пользуясь приведенной выше методикой для дифференцирующей RC-цепи:

tи = t2 – t1 =t*ln (Е⁰ - Е¹) / ( Е⁰ - Uпор),

здесь t = R2*C1.

Относительно инверсного выхода (Uвых2) можно сказать, что на нем в данном состоянии схемы формируется пауза инверсной импульсной последовательности (tп), длительность которой естественно равна tи.

В момент времени t2 напряжение на прямом выходе скачком изменяется до низкого уровня (Е⁰), полярность напряжения на входе ЛЭ2 изменяется на противоположную и его величина равна напряжению, накопленному конденсатором С1. Конденсатор С1 перезаряжается до напряжения с уровнем Е⁰ по цепи: «+»С1 – выход ЛЭ1 – общая точка – VD2 – «-»С1. Время «восстановления» конденсатора определяется аналогично с таковым для дифференцирующей цепи одновибратора:

tвосст.1 = 3*t_раз. = 3*С1*(Rд.пр.+ Rвых.ЛЭ1).

Логический элемент ЛЭ2 по выходу скачком переходит в состояние высокого уровня напряжения Е¹ и схема переходит в состояние второго квазиустойчивого равновесия. В этом состоянии формируется пауза импульсной последовательности на прямом выходе tп и длительность импульса инверсной последовательности t¢и, очевидно, что в этом случае:

tп = t¢и = t3 – t2 =t*ln (Е⁰ - Е¹) / ( Е⁰ - Uпор),

здесь t = R1*C2.

В момент времени t3 напряжение на входе ЛЭ1 достигает порогового значения и напряжения на выходах ЛЭ1 и ЛЭ2 скачком переходят в противоположные состояния (Е¹ и Е⁰ соответственно), далее процессы повторяются. Время восстановления напряжения на конденсаторе С2 определяется аналогично предыдущему случаю:

tвосст.2 = 3*t_раз. = 3*С2*(Rд.пр.+ Rвых.ЛЭ2).

В приведенном примере показана некоторая величина скважности последовательностей импульсов (на временных диаграммах Q≈3 для обычно используемой прямой последовательности). По определению скважность равна:

Q = 1 + tп/ tи = 1 +( R1*C2)/( R2*C1),

Таким образом, для получения Q = 3 необходимо иметь соотношение резисторов в виде R1/R2 = 2 при одинаковых ёмкостях конденсаторов, или соотношение С2/С1 = 2 при одинаковых резисторах. Оба способа пригодны для схемы с логическими элементами КМОП серии, обладающей большими входными сопротивлениями, что позволяет варьировать в широких пределах резисторами времязадающих цепей. Для схем на логических элементах ТТЛ серии величины этих резисторов, как это показано выше, ограничены сверху из-за относительно больших входных токов при логическом нуле на входе, поэтому предпочтительнее способ с установкой разных по величине ёмкости конденсаторов.

Очевидно, что при полной симметрии времязадающих RC-цепей выходная последовательность импульсов будет иметь скважность равную двум (меандр).

Мультивибратор с «мягким» возбуждением отличается от рассмотренного выше наличием дополнительных логических элементов, предотвращающих «засыпание» схемы, т.е. теоретически возможный режим, когда на обеих выходах мультивибратора вместо чередующихся логических нулей или единиц появляется и удерживается «неправильная» комбинация: два логических нуля или две единицы. Схема такого мультивибратора приведена на рис.126.

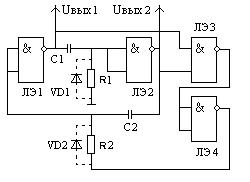
Рис.126

Мультивибратор с мягким возбуждением

При правильном чередовании логических сигналов на входе ЛЭ3, на его выходе всегда будет логическая единица и, следовательно, на выходе ЛЭ4 логический нуль, т.е.нижний вывод резистора R2 через низкое выходное сопротивление ЛЭ4 подключен фактически к общей точке схемы. В этом случае схема не отличается от предыдущей, если же, например, на входе ЛЭ3 две логические единицы, то на его выходе логический нуль и на выходе ЛЭ4 логическая единица, соответствующий ей высокий уровень напряжения переводит ЛЭ1 в состояние логического нуля на выходе и , таким образом, восстанавливаются условия для автоколебаний.