13.Гидравлический и тепловой пограничные слои, турбулентность.

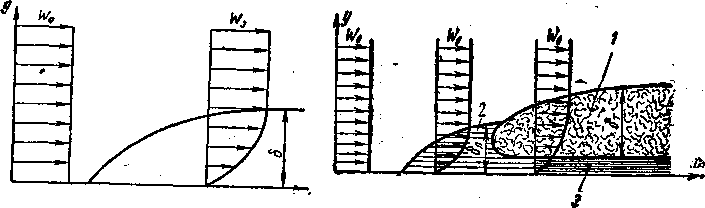
Рассмотрим процесс продольного смывания какого-либо тела безграничным потоком жидкости с постоянной скоростью течения w (рис. 1). Вследствие влияния сил трения в непосредственной близости от поверхности тела скорость течения должна очень быстро падать до нуля. Тонкий слой жидкости вблизи поверхности тела, в котором происходит изменение скорости жидкости от значения скорости невозмущенного потока вдали от стенки до нуля непосредственно на стенке, называется гидродинамическим пограничным слоем (рис. 1). Толщина этого слоя δ возрастает вдоль по потоку.

С увеличением скорости потока толщина динамического пограничного слоя уменьшается вследствие сдувания его потоком. Напротив, с увеличением вязкости толщина динамического слоя увеличивается. Течение в динамическом пограничном слое может быть как турбулентным 1, так и ламинарным 2 (рис.2). Характер течения и толщина в нем (δ_л и δ_Т) определяются в основном величиной числа Re.

 

 

Необходимо отметить, что в случае турбулентного динамического пограничного слоя непосредственно у стенки имеется очень тонкий слой жидкости, движение в котором имеет ламинарный характер. Этот слой называют вязким, или ламинарным, подслоем 3.

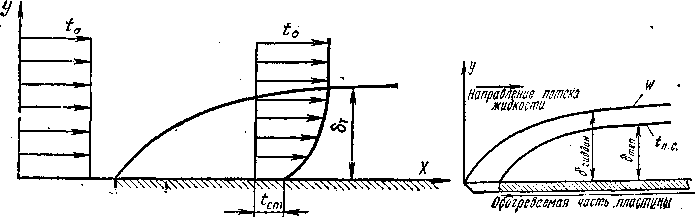
Если температуры стенки и жидкости неодинаковы, то вблизи стенки образуется тепловой пограничный слой, в котором происходит все изменение температуры жидкости (рис. 3). Вне пограничного слоя температура жидкости постоянна t₀. В общем случае толщины теплового и динамического слоев могут не совпадать (рис. 4). Соотношение толщин гидродинамического и теплового пограничных слоев определяется величиной безразмерного числа Рг = v/a. Для вязких жидкостей с низкой теплопроводностью (например, масел) Рг > 1 и толщина гидродинамического пограничного слоя больше толщины теплового пограничного слоя. Для газов Рг ≈ 1 и толщины слоев приблизительно одинаковы. Для жидких металлов Рг < 1 и тепловой пограничный слой проникает в область динамического невозмущенного потока.

14.Теория подобия и его уравнение

С помощью теории подобия размерные физические величины можно объединить в безразмерные комплексы, причем так, что число ком­плексов будет меньше числа величин, из которых составлены эти ком­плексы. Полученные безразмерные комплексы можно рассматривать как новые переменные.

При введении в уравнения безразмерных комплексов число величин под знаком искомой функции формально сокращается, что упрощает иссле­дование физических процессов. Кроме того, новые безразмерные перемен­ные отражают влияние не только отдельных факторов, но и их совокуп­ности, что позволяет легче определить физические связи в исследуемом процессе.

Теория подобия устанавливает также условия, при которых резуль­таты лабораторных исследований можно распространить на другие явле­ния, подобные рассматриваемому. Ввиду этого теория подобия прежде всего "является теоретической базой эксперимента, а также важным под­спорьем теоретических исследований. Хотя методами теории подобия вид искомой функции не может быть определен, эта теория облегчает в ряде случаев анализ процесса и описание полученных результатов.

Для практического использования выводов теории подобия необходимо уметь приводить к безразмерному виду математические описания изучае­мых процессов.

Имеется несколько методов выполнения этой операции. Мы восполь­зуемся одним из них — методом масштабных преобразований.

Первая теорема подобия: если физические процессы подобны между собой, то одноименные числа подобия попарно имеют одинаковые значения.

Числом подобия называют безразмерный комплекс, составленный из величин, существенных для данного процесса. Конкретные числовые значения координаты, скорости, температуры, безразмерные числа в условиях — все это числа подобия; вместе с тем координаты, скорость и температура в безразмерном ви­де, безразмерное давление (число Эйлера) одновремен­но являются безразмерными переменными (аргумента­ми и функциями).

Вторая теорема подобия: решения дифференциальных уравнений, описывающих физический процесс, можно представить в виде зависимости между числами подобия.

В уравнении подобия различают опре­деляющие числа подобия, содержащие независимую пе­ременную (например, безразмерные координаты, безраз­мерное время в нестационарных процессах), и определя­емое число подобия, содержащее зависимую переменную (искомую величину); определяемые числа подобия — Nu, Eu и т. д.

Функциональную связь между определяемыми и определяющими критериями называют уравнениями подобия. Для расчета безразмерного коэффициента теплоотдачи – критерия Нуссельта в стационарных задачах конвективного теплообмена используют следующие уравнения подобия:

– свободная конвекция;

– вынужденная конвекция (ламинарный режим течения);

– вынужденная конвекция (переходный и турбулентный режимы течения),

где – среднее по всей поверхности теплообмена значение критерия Нуссельта.

Уравнения подобия получают в два этапа. На первом этапе строят физическую модель процесса, соблюдая правила моделирования, и выполняют эксперимент на модели. В модели и объекте моделирования добиваются равенства определяющих критериев. Например:

и т.д.,

где индекс "мод" означает "модель", а индекс "обр" – "образец" или объект моделирования.

На втором этапе моделирования выполняют статистическую обработку результатов эксперимента, рассчитывают коэффициент теплоотдачи по закону Ньютона и получают конкретный вид уравнений подобия или т.н. критериальные уравнения, используя правило теории подобия:

или .

При построении модели и обработке результатов эксперимента в виде критериальных формул необходимо задать определяющие параметры, которые прямо или косвенно входят в критерии подобия. В стационарных задачах конвективного теплообмена к определяющим параметрам относят: определяющий размер ( ), определяющую температуру (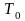 ) и в задачах вынужденной конвекции – определяющую скорость (w₀). Теория подобия не дает однозначного ответа на вопрос: "Какие величины принимать в качестве определяющих параметров?" Поэтому эту задачу решает сам ученый – автор критериального уравнения.

В качестве определяющего размера принимают тот размер системы конвективного теплообмена, от которого зависит конвекция. Например, при свободной конвекции около вертикальных поверхностей в качестве логично принять высоту объекта ( ), а при вынужденном течении в трубах – внутренний диаметр трубы ( ).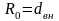

В качестве определяющей температуры, как правило, принимают температуру, которую несложно измерить или рассчитать. За определяющую температуру чаще всего принимают средние температуры в системе теплообмена (в трубах и каналах, в трубных пучках и т.д.) – , температуру флюида за пределами теплового пограничного слоя – и среднюю температуру пограничного слоя – .

Определяющую скорость находят из уравнения неразрывности:

,

где G – расход флюида, кг/c; – плотность, кг/м³; f – площадь поперечного сечения для прохода теплоносителя, м².

При использовании критериальных уравнений определяющие параметры необходимо принимать точно так же, как это сделал автор формулы. Назначенные автором характерные или определяющие параметры , и указывают в комментариях к критериальной формуле.

Конкретный вид функциональной зависимости в уравнениях подобия задает ученый – автор формулы. В принципе для аппроксимации экспериментальных данных можно использовать любую полиноминальную зависимость. В отечественной литературе, как правило, в качестве аппроксимирующих уравнений применяют степенные функции вида:

— – свободная конвекция;

— – вынужденная конвекция (ламинарный режим течения);

— – вынужденная конвекция (переходный и турбулентный режимы течения),

где с, n, m, k – эмпирические коэффициенты, которые находят путем статистической обработки экспериментальных данных;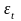 – поправка, учитывающая зависимость физических свойств флюида от температуры; – поправка, учитывающая особенности течения и теплообмена в заданной системе тел.

.