6. Теплопроводность цилиндрической стенки, граничные условия 1 рода для многослойной стенки.

Для многослойной цилиндрической стенки .

Температура на границе двух любых слоев равна: .

7. Теплопередача через цилиндрическую стенку (граничные условия 3-его рода).

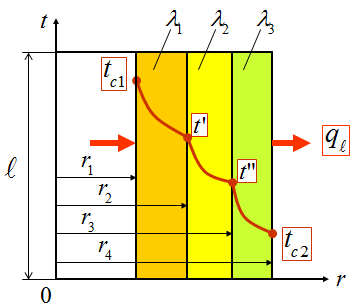
Рассмотрим однородную цилиндрическую стенку большой длины с внутренним диаметром d₁, наружным диаметром d₂ и постоянной теплопроводностью. Заданы значения температуры горячей t_ж1 и холодной t_ж2 среды и коэффициенты теплоотдачи ₁ и ₂. для стационарного режима можно записать:

; ;

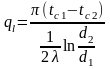где - линейный коэффициент теплопередачи, характеризует интенсивность передачи теплоты от одной жидкости к другой через разделяющую их стенку; численно равен количеству теплоты, которое проходит от одной среды к ругой через стенку трубы длиной 1м в единицу времени при разности температур между ними в 1К.

Величина, обратная линейному коэффициенту теплопередачи, называется линейным термическим сопротивлением теплопередаче.

Для многослойной стенки линейное термическое сопротивление теплопередаче складывается из линейных сопротивлений теплоотдаче и суммы линейных термических сопротивлений теплопроводности слоев.

Температуры на границе между слоями:

8. Теплопроводность плоской пластины при наличии внутренних источников теплоты

При наличии внутренних источников (стоков) теплоты основной задачей является расчет температурного поля внутри тела.

Теплопроводность плоской стенки при наличии внутренних источников теплоты

Теплопроводность плоской стенки. Рассмотрим однородную плоскую стенку толщиной , коэффициент теплопроводности  которой постоянен. Внутри этой стенки имеются равномерно распределенные источники теплоты . Выделившаяся теплота через боковые поверхности стенки передается в окружающую среду. Относительно площади стенки в среднем сечении процесс теплопроводности будет протекать симметрично, поэтому именно здесь целесообразно поместить начало координат, а ось х направить перпендикулярно боковым поверхностям (рис. 1-15). Из уравнения теплового баланса следует, что при наличии внутренних источников теплоты плотность теплового потока в плоской стенке линейно возрастает с увеличением х и равна:

Из этого уравнения видно, что при , а при , т. е. достигает своего максимального значения. Согласно закону Фурье

Произведя разделение переменных, имеем:

Интегрируя это уравнение, получаем:

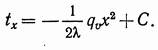
Постоянная интегрирования С определяется из граничных условий. При уравнение изменения температуры принимает вид:

Из уравнения следует:

Здесь разность  означает перепад температуры между серединой и внешними поверхностями плоской стенки,  — плотность теплового потока на этих граничных поверхностях. Если температура неизвестна, то значение постоянной С можно выразить через и уравнение температурной кривой в этом случае принимает вид:

Приведенные выводы показывают, что при наличии равномерно распределенных внутренних источников теплоты распределение температур в плоской стенке носит параболический характер. Наибольшее значение температура имеет в средней плоскости .

Теплопроводность круглого стержня при наличии внутренних источников теплоты.

При больших перепадах температуры необходимо учитывать зависимость коэффициента теплопроводности от температуры, . В этом случае уравнение (в) принимает следующий вид:

Интегрируя уравнение, получаем:

Подставляя значение С в уравнение (е) и решая последнее относительно t, получаем следующее уравнение температурной кривой: