Дилемма. Виды дилемм
Дилемма,
заключение которой является следствием
условных посылок или отрицанием их
основания
Дилемма,
в заключение которой входят следствия
условных посылок
Дилемма,
заключением которой является дизъюнкция
следствий условных посылок
или
отрицаний
их оснований
Дилемма,
в заключение которой входят отрицания
оснований условных посылок
Сложная
Конструктивная
ДеструктивнаяПростая
Дилемма,
в заключение которой входят
следствия
условных посылок
Классификация дилемм
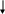
Схема 44.
СХЕМА 45.
ЗАНЯТИЕ 4/4. Практическое занятие.
«Дедукция и ее роль в мышлении»
Время -2 часа.
Цели занятия:
1. Углубить и закрепить знания теоретических положений по изучаемой теме.
2. Сформировать навыки выполнения умозаключений из двух простых суждений.
3. Получить практику достижения истинного вывода в ПКС, опираясь на знания его общих правил, правил фигур и правильных модусов каждой фигуры.
4. Научиться делать истинные выводы из сложных суждений.
Содержание занятия:
Основная часть
Вопрос 1. Общая характеристика простого категорического силлогизма
определение ПКС;
разбор ПКС: понятие о крайних терминах, меньшем и большем терминах, меньшей и большей посылках;
средний термин ПКС и его значение;
аксиома ПКС.
Вопрос 2. Правила терминов и посылок силлогизма.
общие правила ПКС: правила терминов и правила посылок;
фигуры ПКС, правила фигур;
модусы ПКС, значение правильных модусов.
Вопрос 3. Выводы из сложных суждений и их роль в мышлении.
чисто условное умозаключение;
условно-категорическое умозаключение;
разделительно-категорическое умозаключение;
условно-разделительные (лемматические) умозаключения.
II. Контрольный опрос. (Проверка теоретических знаний. Может проводиться как в устной, так и в письменной форме).
1. ПКС: сущность и структура.
2. Общие правила ПКС: правила терминов, правила посылок.
3. Фигуры и модусы ПКС. Частные правила фигур.
4. Чисто условное умозаключение.
5. Условно-категорическое умозаключение и его правильные модусы.
6. Разделительно-категорическое умозаключение и его модусы
7. Лемматические умозаключения. Дилемма и ее виды.
III. Дидактический тренинг. (Решение задач и упражнений).
Образцы решения задач и упражнений.
Задача: Сделайте вывод из посылок. С помощью общих правил ПКС, частных правил фигур и модусов ПКС установите, следует ли заключение с необходимостью.
Примеры:
а) А: Все спасатели (Р+) являются мужественными людьми (М–).
А:
Все офицеры (S+)–
мужественные люди (M–)
?
Решение:
1. Опираясь на первое правило терминов (в ПКС должно быть только три термина, средний термин должен быть взят в одном значении), приходим к выводу о возможности связи крайних терминов. Следовательно, данное правило соблюдено. Заключением из приведённых посылок будет суждение
«Все офицеры – спасатели».
2. Однако мы не убеждены в его истинности. Что бы развеять или подтвердить сомнения, необходимо продолжить анализ данного ПКС по другим правилам.
3. Второе правило терминов гласит: «Средний термин должен быть распределён хотя бы в одной из посылок». В противном случае он не сможет выполнить свою функцию – связать крайние термины в заключении.
В нашем примере каждая из посылок является общеутвердительным суждением (А). Средний термин (М) выполняет роль предиката в большей и меньшей посылках. А нам уже известно (см. «распределённость терминов в суждениях»), что предикат в утвердительных суждениях не распределён, следовательно, не распределён и средний термин ни в одной из посылок в нашем примере. Таким образом, второе правило запрещает признать истинность заключения:
«Все офицеры – спасатели».
4. Невозможность получения истинных заключений в подобных случаях подтверждается так же правилами фигуры данного силлогизма:
В нашем примере мы имеем дело со второй фигурой ПКС
Р
M
S М
Её правила:
1) Большая посылка должна быть общим суждением.
2) Одна из посылок должна быть отрицательным суждением.
Опираясь на данные правила, обнаруживаем, что в анализируемом примере нет отрицательной посылки, следовательно, и по этому основанию, т.е. по правилам второй фигуры, нельзя признать напрашивающееся заключение «Все офицеры – спасатели» истинным.
5. Помимо перечисленных, логика даёт нам ещё одну возможность проверки истинности заключения – обратиться к правильным модусам второй фигуры. Модуса ААА (''barbara'') среди правильных модусов второй фигуры нет, следовательно, и по этому основанию признать истинным заключение: «Все офицеры – спасатели» возможности нет.
б). I: Некоторые упражнения по логике вызывают затруднение.
I
:
Некоторые упражнения по логике связаны
с выяснением объёмных отношений между
понятиями
?
Решение:
1. Обе посылки являются частноутвердительными суждениями, следовательно, истинный вывод из них невозможен. (См. правила посылок ПКС).
в) А: Все преподаватели кафедры философии М+ имеют учёную степень (р-).
А
:
Все преподаватели кафедры философии
(М+)
– профессора (S–-)
?
Решение:
Из общих суждений в посылках мы вынуждены сделать частное заключение (I). Некоторые профессора (S-) имеют учёную степень (Р-).
В данном случае вступает в силу правило крайних терминов: термин, не распределённый в посылке, не может быть распределён и в заключении.
Пример:
А: Коса (М+) – девичья краса (Р–)
А: Коса (М+) – это сельскохозяйственный инструмент (S-)
?
Решение:
1. Давая логическую характеристику суждениям, обнаруживаем общий для них термин «коса», что позволяет нам связать крайние термины в заключении. Придерживаясь уже известного нам правила: «термин, не распределенный в посылке, не может быть распределен и в заключении» формулируем частноутвердительное заключение:
I: Некоторые сельскохозяйственные инструменты(S-) украшают девицу (P-).
2. Сформулированное суждение кажется нелепостью. Но не будем гадать. Логика требует опоры на правила, одно из которых звучит следующим образом: «в ПКС должно быть только три термина, при этом средний термин должен быть взят лишь в одном и том же смысловом значении».
В нашем примере термин «коса» в первой посылке мыслится как волосы, растущие на голове, а во втором суждении – как сельскохозяйственный инструмент. В нарушение правила произошла ошибка: «учетверение терминов».
Таким образом, заключение:
I: Некоторые сельскохозяйственные инструменты (S-) украшают девицу (P-).
Не является истинным.
Задача: Найдите основание и следствие в условных посылках, сделайте вывод, постройте его схему. Если условная посылка явно не выражена, сформулируйте её в явной логической форме (со связкой ''если…, то…'').
Пример:
Если заседание совета состоится сегодня (р), то завтра мы сможем переоборудовать цех (q). В таком случае выпуск новой продукции начнётся уже на следующей неделе (r).
Решение:
1. Первое суждение является условным, где:
- ''Заседание совета состоится сегодня'' – основание суждения (р);
- ''Завтра мы сможем переоборудовать цех'' – следствие суждения (q);
- Символическая запись суждения: (р q).
2. Во втором суждении основание явно не выражено. Выражение «в таком случае» подразумевает следствие первого суждения (q). В явной логической форме (со связкой '' если…, то… '') его можно представить следующим образом:
''Если завтра мы сможем переоборудовать цех (q), то выпуск новой продукции начнётся уже на следующей неделе (r), где:
- ''Завтра мы сможем переоборудовать цех '' – основание данного суждения (q);
- ''выпуск новой продукции начнётся уже на следующей неделе'' – следствие суждения (q).
3. Из явных условных посылок строим умозаключение:
Е
сли
заседание совета состоится сегодня
(p),
то завтра мы сможем переоборудовать
цех (q).
Е
сли
завтра мы сможем переоборудовать цех
(q)
, то выпуск новой продукции начнётся
уже на следующей неделе (r).
Если заседание совета состоится сегодня (p), то выпуск новой продукции начнётся уже на следующей неделе (r).
С
хема
вывода: (p→q)(q→r)
p→r
Задача: Используя условную посылку, постройте умозаключения по каждому из возможных модусов, запишите их схемы, укажите правильные модусы. Если условная посылка явно не выражена, сформулируйте её в явной логической форме (со связкой '' если…, то…).
Пример:
Река, вышедшая из берегов, заливает водой прилегающие территории.
Решение:
Приведём данное суждение к явной логической форме (со связкой '' если…, то…).
Если река выходит из берегов (р), то вода заливает прилегающие территории (q). p → q
2. Строим умозаключение по каждому из возможных модусов:
а) Если река выходит из берегов (p), то вода заливает прилегающие территории (q).
Р
ека
выходит из берегов (p).
Вода заливает прилегающие территории (q).
Схема вывода:
p
→ q , p
q – Модус правильный
б) Если река выходит из берегов (p), то вода заливает прилегающие территории (q).
Р
ека
не выходит из берегов (
p)
?
С
Модус
неправильный.
Могут быть
и другие причины того, что прилегающие
к реке территории заливает вода
p
→ q,
p
?
в) Если река выходит из берегов (р), то вода заливает прилегающие территории (q).
Вода
заливает прилегающие территории.(q)
?
Схема вывода:
p → q , p
?
Модус неправильный. У одного и того же
следствия могут быть разные основания.
г) Если река выходит из берегов (p), то вода заливает прилегающие территории (q).
В
ода
не заливает прилегающие территории
.
Река не выходит из
берегов.
Схема вывода:
p → q , p
?
Модус правильный. Вывод следует с необходимостью.
Задача: Сделайте вывод из посылки разделительно – категорического умозаключения, определите модус, постройте его схему, укажите вид дизъюнкции: строгая или нестрогая, полная или неполная.
Пример:
Пожар возник или вследствие нарушения правил пожарной безопасности (р.), или в результате стихийного бедствия (q) , или поджога (r). Другой причины быть не могло.
Решение:
Установлено, что пожар возник в результате поджога (r).
Результатом вывода из данных посылок будет следующее суждение:
Неверно, что пожар возник вследствие нарушения правил пожарной безопасности или в результате стихийного бедствия.
Схема вывода:
р q
r
, r
- утверждающе –
отрицающий модус;
р; q - дизъюнкция полная, строгая.
Задача: Используя условные посылки, постройте умозаключение в форме дилеммы. Определите ее вид, запишите формулу дилеммы.
Пример:
«Возвеличит молва (m) – то вина не твоя (n).
Полетит голова (p) – то вина не твоя (n)» (О. Хайям)
Решение:
1. В данном примере два разных основания в условных посылках «возвеличит молва (m)» и «полетит голова (p)» ведут к одному и тому же следствию: «вина не твоя (n)»
2. Для построения умозаключения в форме дилеммы необходимо сформулировать третью посылку, которая должна быть сложным разделительным суждением и в которой будем утверждать истинность оснований условных посылок.
Либо молва возвеличит (m), либо полетит голова (p).
3. В заключении приходим к простому категорическому суждению, в котором утверждается истинность следствия условных посылок.
Вина не твоя (n).
Рассуждение приобретает следующий вид:
«Возвеличит молва (m) – то вина не твоя (n).
Полетит голова (p) – то вина не твоя (n)» (О. Хайям)
Либо молва возвеличит (m), либо полетит голова (p).
Вина не твоя (n).
4. Данное умозаключение является простой конструктивной дилеммой. Формула умозаключения:
m → n
p → n
m p
n
Пример:
«Когда б мне власть была дана (m), вершинам всем, являя разум,
Я даровал бы в мире разом любимых женщин имена (n).
Когда б мне власть была дана (m), неся ответственность пред веком,
Я матерей бы имена присвоил пограничным рекам (q)» (Р. Гамзатов)
Решение:
1.В данном примере одно и то же основание в двух условных посылках «мне власть была дана (m) ведет к двум разным следствиям (n и q).
2. Для построения умозаключения в форме дилеммы необходимо сформулировать третью посылку, которая должна быть сложным разделительным суждением и в которой будем отрицать истинность следствий условных посылок.
Но я не смог сделать то (Øn) или другое (Øq)
3. В заключении приходим к простому категорическому суждению, в котором отрицается истинность оснований условных посылок.
Мне не дано было власти (Øm)
4. Рассуждение приобретает следующий вид:
«Когда б мне власть была дана (m), вершинам всем, являя разум,
Я даровал бы в мире разом любимых женщин имена (n).
Когда б мне власть была дана (m), неся ответственность пред веком,
Я матерей бы имена присвоил пограничным рекам (q)» (Р. Гамзатов)
Но я не смог сделать то (Øn) или другое (Øq)
Мне не дано было власти (Øm)
5. Данное умозаключение является простой деструктивной дилеммой. Формула умозаключения:
m → n
m → q
Øn Øq
Øm
Пример:
«Кто удачно нашел себе зятя (m), приобрел сына (p), а кто неудачно (n), потерял также и дочь (q)» (Демокрит)
Решение:
1.В этом высказывании Демокрита разные основания в двух условных посылках «удачно нашел себе зятя (m), и «неудачно нашел себе зятя (n), ведут к двум разным следствиям «приобрел сына (p)» и «потерял также и дочь (q)» .
2. Для построения умозаключения в форме дилеммы необходимо сформулировать третью посылку, которая должна быть сложным разделительным суждением и в которой будем утверждать истинность следствий условных посылок.
Зять может быть удачным (m) или неудачным (n).
3. В заключении приходим к сложному разделительному суждению, в котором утверждается истинность следствий условных посылок.
Приобретешь сына (p) или потеряешь дочь (q).
4. Рассуждение приобретает следующий вид:
«Кто удачно нашел себе зятя (m), приобрел сына (p), а кто неудачно (n), потерял также и дочь (q)» (Демокрит)
Зять может быть удачным (m) или неудачным (n).
Приобретешь сына (p) или потеряешь дочь (q).
5. Данное умозаключение является сложной конструктивной дилеммой. Формула умозаключения:
m → p
n → q
m n
p q
Пример:
«Не будь сумы на свете да тюрьмы (m),
Я стал бы оптимистом самым рьяным (p).
Когда бы все бессмертны были мы (n),
Я был бы атеистом самым рьяным (q)» (Р. Гамзатов)
Я – не самый рьяный оптимист (p) или не самый рьяный атеист (g)
Либо на свете нет сумы или тюрьмы (m), либо все мы смертны (n).
Решение:
1.В данном четверостишии разные основания в двух условных посылках «Не будь сумы на свете да тюрьмы (m), и «все бессмертны были мы (n), ведут к двум разным следствиям «Я стал бы оптимистом самым рьяным (p)» и «Я был бы атеистом самым рьяным (q)» .
2. Для построения умозаключения в форме дилеммы необходимо сформулировать третью посылку, которая должна быть сложным разделительным суждением и в которой будем отрицать истинность следствий условных посылок.
Я – не самый рьяный оптимист (p) или не самый рьяный атеист (q)
3. В заключении приходим к сложному разделительному суждению, в котором отрицается истинность оснований условных посылок.
Либо на свете нет сумы или тюрьмы (m), либо все мы смертны (n).
4. Рассуждение приобретает следующий вид:
«Не будь сумы на свете да тюрьмы (m),
Я стал бы оптимистом самым рьяным (p).
Когда бы все бессмертны были мы (n),
Я был бы атеистом самым рьяным (q)» (Р. Гамзатов)
Я – не самый рьяный оптимист (p) или не самый рьяный атеист (q)
Либо на свете нет сумы или тюрьмы (m), либо все мы смертны (n).
5. Данное умозаключение является сложной деструктивной дилеммой. Формула умозаключения:
m → p
n → q
p q
m n