VII. Расчёт и построение рабочей области в системе matlab

Исходными данными для расчета являются численные значения для

коэффициентов K1 ÷ K5, которые рассчитываются по формулам (25) .

При расчете по каждому уравнению рассчитываются значения

коэффициента усиления К_ЭУ при пошаговом изменении в некотором диапазоне

постоянной времени Т_ОС. При выборе диапазона необходимо

ориентироваться на заданную величину времени переходного процесса – t_п. В

данном задании t_п = 15с. Поэтому диапазон изменения постоянной Т_ОС не

должен превышать 9 с При этом значения коэффициента усиления,

рассчитанные по первому уравнению обозначаются символом К_ЭУ1, по второму

уравнению – символом К_ЭУ2 и т. д. После окончания расчета в системе координат

К_ЭУ, Т_ОС строятся кривые границ, и выделяется рабочая область.

Программа для расчёта сдержит 55 строк. Ниже представлен текст программы.

km = 100

k1 = 5000

k2 = 80 * (1 + km)

k3 = 5000 * (1 + km)

k4 = 1 + km

k5 = 0.61 * 10^-3 * km

% 1 граница

t1 = 0.1:.01:6;

ke1 = (6*(t1+k3).^2-k1*k4*t1-k2*k4)./(t1.*(k1*k5*t1+k2*k5));

% 2 граница

t2 = 0.1:.01:6;

ke2 = (t2+k3).^3./((k1*t2+k2).^2*k5);

% 3 граница

t3 = 0.1:.01:6;

ke3 = 0.5*k4*(t3+k3)./(k5*(t3*k1+k2-0.5*t3.^2-0.5*t3*k3));

% 4 граница

t4 = 0.1:.01:6;

b = k5*(12*k4*t4-t4-k3);

c = 6*k4^2;

a = 6*t4.^2*k5^2;

ke4 = (-b+sqrt(b.^2-4*a*c))./(2*a);

% разделительная линия

t0 = 0.1:.01:6;

a0 = 0.75*t0.^2*k5^2;

b0 = 1.5*k4*k5*t0-k5.*(t0+k3)*0.75;

c0 = 0.75*k4^2;

ke0 = (-b0+sqrt(b0.^2-4*c0*a0))./(2*a0);

% линия tп=tзад

tzad=15;

ke5 = -1*10.^8:1*10.^6:4*10.^8;

t5 = (tzad-(3*k4./(k5*ke5)))./3;

% вывод графиков

plot(t1,ke1,t2,ke2,t3,ke3,t4,ke4,t0,ke0,t5,ke5);

% координаты надписей над кривыми

text(0.42, 1*10^10, 'ke1');

text(0.55, 2.3*10^10, 'ke2');

text(0.22, -0.1*10^10, 'ke3');

text(0.35, 0.1*10^10, 'ke4');

text(0.02, 0.28*10^10, 'p=1');

text(3, 0.15*10^10, 'work areas');

text(7.9, 0.15*10^10, 'tp=tzad');

% контроль принадлежности к рабочей области

toc = 5

ke = 5*10^7;

a0 = k1*toc+k2;

a1 = toc+k3;

a2 = k4+toc*ke*k5;

a3 = k5*ke;

raz1 = a0*a2-6*a1^2

raz2 = a0^2*a3-a1^3

raz3 = a0*a3-0.5*a1*a2

raz4 = a1*a3-6*a2^2

% вычисление po, tp

po = (a3*a1)/(0.75*a2^2)

tp = 3*a2/a3

После выполнения программы получены следующие данные:

km =100

k1 =5000

k2 =8080

k3 =505000

k4 =101

k5 =0.0610

toc =5

raz1 = -1.0257e+012

raz2 = -1.2545e+017

raz3 = -3.7498e+012

raz4 = -1.3939e+015

po = 0.0088

tp =15.0001

И график рабочей области

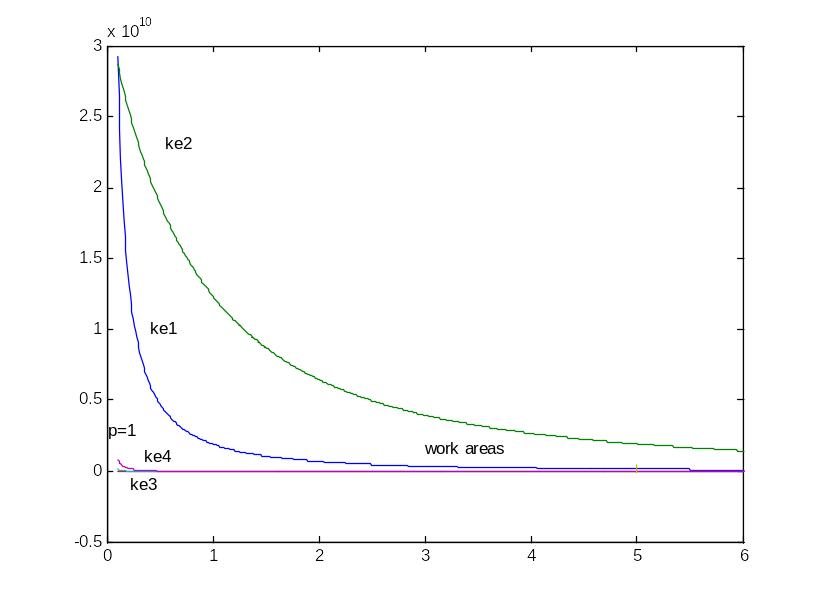
Первые шесть строк содержат сведения о коэффициентах.

В строках 8–9, 11–12, 14–15, 17–21 размещены формулы для расчета

коэффициентов усиления КЭУ1, КЭУ2, КЭУ3, КЭУ4 при пошаговом изменении

постоянной времени корректирующего элемента T_OC. При этом, параметр T_OC в

программе обозначен символом «t» c индексом, совпадающим с номером

рассматриваемого уравнения. Так, в строках 8–9 применено обозначение t1, в

строках 11–12 – обозначение t2 и т. д. Коэффициенты усиления в программе

имеют обозначения ke1, kе2, ке3, ке4. В строках 18, 19, 20 определяются

промежуточные коэффициенты «а, b, с» для расчета К_ЭУ4. В строках 23–27

рассчитывается кривая, разделяющая рабочую область на подобласти

колебательных и апериодических процессов. Для расчетов применена формула р=a₁*a₃/0.75*a₂^2 (28). Далее, если в принять ρ = 1 и записать полученное равенство относительно коэффициента усиления КЭУ, то полученное выражение будет являться уравнением искомой разделительной кривой. Данное уравнение имеет вид

Если принять обозначения:

т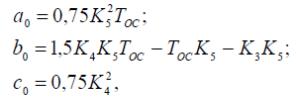 о решение уравнения запишется в виде

В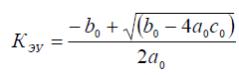 программе постоянная времени T_ОС и коэффициент усиления К_ЭУ,

соответствующий разделительной кривой ρ = 1, обозначены символами t0 и ке0

соответственно.

Таким образом, в первых 27 строках программы выполняются следующие

две операции:

1. Рассчитываются численные значения для коэффициентов К1 ÷К5;

2. Для каждого из четырех уравнений границ рабочей области определяются

массивы чисел необходимые для построения графиков:

ke0 = f(t0);

kе1 = f1(t1);

ke2 = f2(t2);

ke3 = f3(t3);

ke4 = f4(t4);

(29)

При получении массивов значение для постоянная времени T_ОС изменялось с

шагом 0,01 с от 0,1 с до 6с.

Уже понятно, что приведенные в (29) обозначения коэффициентов

отличаются друг от друга только из-за принадлежности к разным графикам.

Фактически все они представляют собой один и тот же коэффициент усиления

САР. Так же и обозначения t0, t1, t2, t3 и t4 соответствуют только

постоянной времени T_ОС.

В строках 30-31 производится построение прямой, на которой будут располагаться все возможные рабочие точки. На этой прямой время переходного процесса равно заданному времени. При этом используется формула

П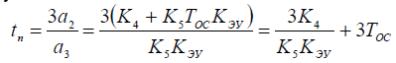 осле подстановки

_tп = 303/0.061*К_эу + 3*Т_ос

Анализируя эту формулу, можно заметить, что первое слагаемое в ней

практически не формирует время t_п, так как в рабочей области величина

коэффициента усиления К_ЭУ находится в диапазоне 10^7÷ 10^8. Второе же

слагаемое вносит существенный вклад в формирование времени переходного

процесса. Если принять К_ЭУ = 5*10^7 и t_П = 15 с (это время определяется заданием), то окажется, что величина постоянной времени Т_ОС = 5 c. Координаты К_ЭУ = 5*10^7, Т_ОС = 5 c определяют место расположения рабочей точки в рабочей области.

Строка 33 организует вывод всех графиков в одном окне. Строки

35–41 организуют надписи над кривыми.

Строки 43–52 организуют проверку существования рабочей области. Для

этого используются неравенства (22), которые в программе записаны в виде

четырех разностей raz1 ÷ raz4. Разности записаны в строках 49–52. В строках

45–48 размещены формулы для расчета коэффициентов уравнения САР. Эти

коэффициенты в программе обозначены прописными буквами a0, a1, a2 и a3. В

строках 43 и 44 задаются координаты точки, проверяемой на принадлежность к

рабочей области. В строке 54 для этой точки рассчитывается значение для

показателя p (если р<1 процесс апериодический, если р>1 - колебательный), а в строке 55 – время переходного процесса.