V. Основные положения метода эффективных полюсов и нулей
Метод эффективных полюсов и нулей (МЭПН) в отличие от других
методов синтеза (например, с использованием логарифмических амплитудных
характеристик (ЛАХ)) ориентирован на преимущественное использование ЭВМ
для решения задач проектирования САР. Метод позволяет решать задачу
оптимизации на ЭВМ заданного критерия качества при наличии большого
количества ограничений и варьируемых параметров. Метод имеет достаточно
простые алгоритмы, что создает возможность не трудоемко выполнить ручные
расчеты показателей качества процессов для определения исходных значений
параметров элементов САР, используемых далее для расчетов на ЭВМ.
Расчеты с использованием МЭПН являются приближенными. Погрешности могут достигать 10-30%. Поэтому на заключительном этапе расчета требуется численное моделирование процессов.
Исходной предпосылкой к применению метода является выполнение требования по колебательности системы. Данное требование имеет вид
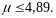(20)
К
олебательность
характеризует запас устойчивости САР
и связана с расположением корней
характеристического уравнения на
комплексной плоскости (рис.10):
(21)
где φк - угол, внутри (и на границах) которого расположены все корни характеристического уравнения системы. На рис.10 показано расположение четырех корней условной системы.
Область изменения параметров элементов системы, где требование (20)
выполняется, называется рабочей областью. Так как переменных параметров в
системе может быть много, то эта область в общем случае ограничивается
многомерной поверхностью. Если переменных параметров два, то рабочая
область будет представлять собой часть плоскости.
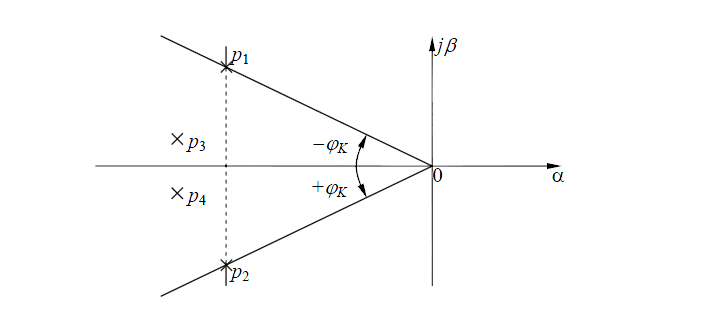
Рис.10. Схема расположения корней
VI. Расчет границ рабочей области
Рабочей является область изменения параметров элементов системы,
внутри которой выполняется требование по запасу устойчивости. Так как
переменных параметров в системе может быть много, то рабочая область в
общем случае ограничивается многомерной поверхностью. Если переменных
параметров два, то рабочая область будет представлять собой часть плоскости.
Именно такой случай имеет место в данном курсовом проекте. Указанная часть
плоскости располагается в системе координат, в которой по одной из осей (ось
ординат) откладывается коэффициент усиления системы , а по другой оси
тот параметр, который наибольшим образом влияет на показатели переходного
процесса. Таким параметром в данном проекте является постоянная времени
корректирующего элемента. Расположение рабочей области в системе
координат ограничивается линиями, называемыми границами. Количество
таких линий-границ зависит от порядка характеристического уравнения
системы. Для системы третьего порядка (19) таких линий-границ четыре.
М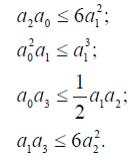
атематически
они представляются следующими
соотношениями:
(22)
В этих соотношениях знак равенства предназначен для описания линий-границ,
а знак неравенства – пространству с той стороны кривой, где выполняются
требования по запасу устойчивости.
Перед началом работы с соотношениями (22) целесообразно определить
численные значения параметров, образующих коэффициенты уравнения (19).
В учебном пособии [1] приведены формулы для расчета параметров. Так,
ф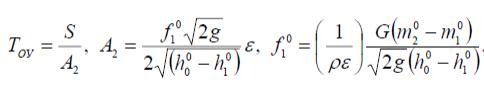
ормулы
для определения постоянной времени
объекта управления имеют
вид:
(23)
Формула для определения площади проходного сечения вентиля на номинальном режиме получена из уравнения равновесного режима. Коэффициент расхода учитывает влияние местных сопротивлений. Для выполнения расчетов целесообразно привести размерности к системе СИ. Выполняем расчет по формулам (23):
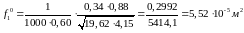
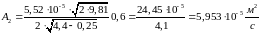
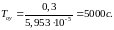
Далее необходимо рассчитать постоянные параметры, входящие в состав
коэффициента передачи разомкнутой системы (16). Переменным параметром
здесь является коэффициент усиления электронного усилителя. Коэффициент
усиления магнитного усилителя задается
КМУ=100
В пособии [1] представлена методика расчета коэффициента передачи измерителя уровня жидкости – КИ. Она достаточно проста, поэтому здесь расчет этого коэффициента не выполняется, а задается. На схеме (рис. 2) выходным сигналом измерителя является напряжение Uh. Выходным сигналом датчика уровня (сильфонного типа) является линейное перемещение свободного конца сильфона.
Следовательно, на схеме (рис. 2) в состав измерителя введена еще и мостовая
электрическая измерительная схема. С учетом этого КИ=0.009*100=0.9
(0.009 – коэффициент передачи сильфона, 100 – коэффициент передачи
мостовой измерительной схемы).
Следующими постоянными параметрами являются коэффициент
передачи объекта управления и коэффициент передачи регулирующего
органа . В пособии [1] приводятся формулы для расчета этих коэффициентов:
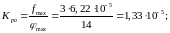
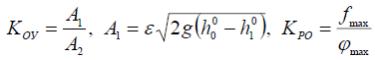
Производим расчёт А1 и Коу
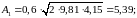
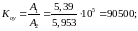
Для расчета параметров KДВ и KРед необходимо знать параметры двигателя. В системах регулирования обычно применяют двигатели постоянного тока с независимым либо другим типом возбуждения. Для выбора двигателя пользуются таблицами, размещаемыми в справочной литературе [1]. Выбор двигателя осуществляют по требуемой мощности, которая рассчитывается по формуле
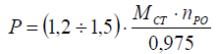
где MСТ – момент статического сопротивления нагрузки, кг*м,
nРО – максимальная частота вращения оси регулирующего органа, об/мин.
P – мощность двигателя, Вт.
Момент MСТ прикладывается к оси регулирующего органа, т. е. к вентилю для его вращения. Поэтому для определения величины момента необходимо знать марку вентиля. Марка вентиля также определяется по справочной литературе. В этой литературе приводятся расходные, геометрические и др. характеристики в том числе и величина MСТ. Чтобы воспользоваться справочником, необходимо знать максимальный расход жидкости через вентиль. В данной работе таким расходом является величина уноса жидкости тканью из рабочей емкости:
Д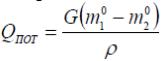
ля
принятых исходных данных
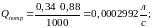
Если расход жидкости изменяется в пределах (0,2 ÷ 0,6) м3, то величину
MСТ можно выбирать из диапазона (1,5 ÷ 2,5) кг·м. Максимальная частота
вращения регулирующего органа nРО рассчитывается по формуле
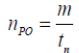
где m – количество оборотов вентиля, совершаемого за время переходного процесса tПП, m=0,2φmax.
Время переходного процесса tПП= 15 с, с учетом φmax = 14 об
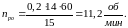
Принимаю MCT=1,9кг*м, и рассчитываю мощность двигателя
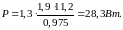
В приложении пособия [1] данной мощности соответствует двигатель
постоянного тока независимого возбуждения СЛ-367. Двигатель имеет
следующие характеристики:
Номинальное напряжение В 110
Полезная мощность Вт 32
Скорость вращения 2500
Ток якоря, А 0,9
Ток обмотки возбуждения, А 0,08
Момент на валу, 0,125
Сопротивление якоря, 1,5
Сопротивление обмотки 1160
возбуждения, Ом
Пусковой момент, 0,220
Момент инерции, 0,07
Вес, кг 2,5
Теперь рассчитываю оставшиеся коэффициенты передач КДВ, КР и постоянную время двигателя TДВ. Для расчета КР необходимо определить передаточное число редуктора i.
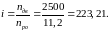
где nРО– скорость вращения регулирующего органа.
Коэффициент передачи редуктора
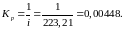
Коэффициент передачи двигателя
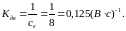
Постоянная времени двигателя
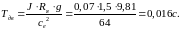
Рассмотрим содержание коэффициентов уравнения (19) с учетом полученных численных значений параметров:
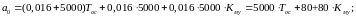
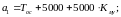
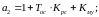
где
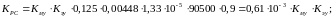
В результате получатся следующие
выражения для коэффициентов уравнения (19):
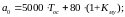
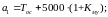
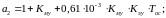
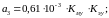(24)
Введем обозначения:
К1 = 5000
К2 = 80*(1+КМУ)
К3 = 5000*(1+КМУ)
К4 = 1+КМУ
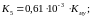(25)
С учетом коэффициентов К1–К5, выражения (24) приобретают простой и
удобный для расчета границ рабочей области вид
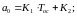
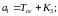
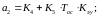
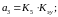(26)
Далее можно получить уравнения границ рабочей области. Для этого
н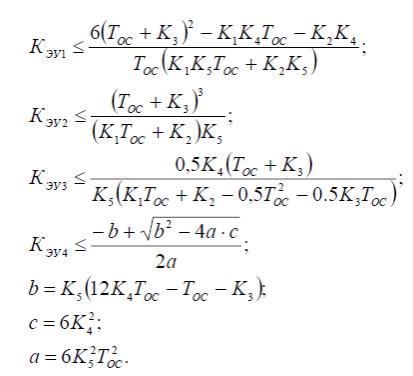
еобходимо
использовать неравенства (22) и выражения
(26). Уравнения имеют
вид
(27)
Выражения (27) становятся уравнениями границ рабочей области при
замене знака «меньше или равно» на знак «равенства». Видно, что границ
должно быть четыре. Ранее уже указывалось, что рабочая область строится в
плоскости изменения двух параметров kЭУ и ТОС. Следовательно, для расчета
кривых, отражающих границы рабочей области необходимо наметить
некоторый диапазон изменения параметра ТОС. Затем этот диапазон разбить на
равные интервалы и для каждой точки, разделяющей смежные интервалы по
формулам (25) и (27) вычислить соответствующие им значения коэффициента
kЭУ. Далее строятся кривые и определяется рабочая область. В данной работе расчёт и построение рабочей области будет производится в системе MATLAB