4. Передаточная функция исполнительного механизма

Мощность от вала двигателя к регулирующему органу передается через редуктор. Редуктор выбирается из стандартного ряда редукторов. В маломощном приводе КПД не является определяющим, поэтому главное при выборе редуктора – его передаточное число.

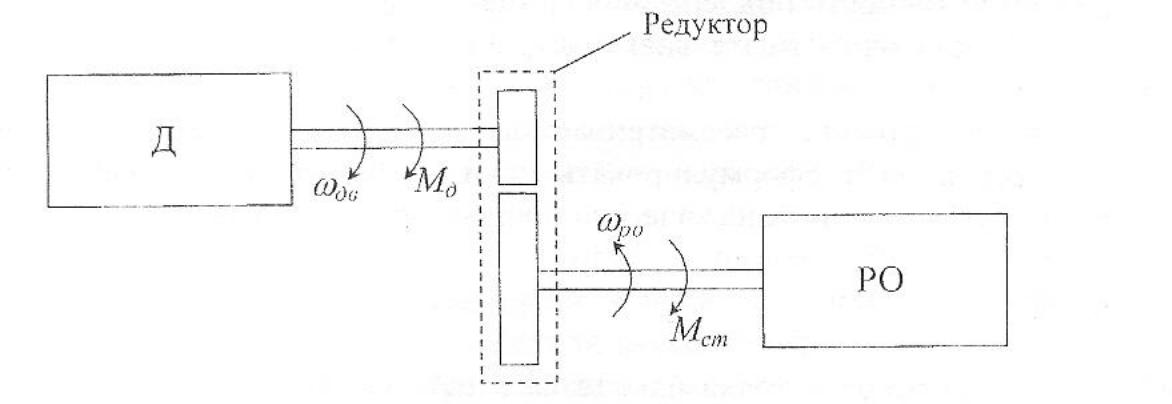
Рис.4. Схема исполнительного механизма

Расчет передаточного числа редуктора i выполняется по формуле

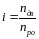
где n_дв – номинальная частота вращения двигателя, .

Величина скорости n_ро определяется из следующих соображений:

предположим, что по требованиям технологического процесса время

регулирования известно и равно t_пп. Предположим также, что регулирующим

органом является перекрывной вентиль, обеспечивающий регулирование

расхода жидкости в емкость. Для выбора вентилей также имеется справочная

литература. Пусть для полного открытия вентиля (исходное положение –

вентиль закрыт) требуется сделать 10 – 15 оборотов. В процессе же регулиро-

вания в течение времени переходного процесса t_пп целесообразно изменять

положение вентиля примерно на угол, соответствующий 3 – 4 оборотам. Это

объясняется тем, что при регулировании расход жидкости через вентиль не

должен сильно изменяться. Можно принять, что максимальное изменение

регулируемой величины (в заданном примере расхода жидкости) не должно

превышать 20 %.

Далее можно определить величину максимальной скорости вращения

вентиля (исполнительной оси регулирующего органа)

Величина максимальной скорости вращения вентиля равно:

,

где m – количество оборотов регулирующего органа, в данном случае m = 3 ÷ 4 оборотам. Коэффициент передачи редуктора как элемента САР рассчитывается по формуле

Редуктор выбирается из стандартного ряда редукторов. В маломощном

приводе к.п.д. не является определяющим, поэтому главное при выборе

редуктора его передаточное число.

Остальные элементы системы (датчики, при необходимости

корректирующие элементы) выбираются по справочникам и каталогам.

5. Передаточная функция регулирующего органа (вентиль).

Регулирующим органом в данном задании служит вентиль. Предполагая его статическую характеристику линейной, передаточную функцию для него можно представить в виде коэффициента передачи

где f_1max - максимальное проходное сечение вентиля;

φ_max - угол поворота вала, при котором происходит полное открытие или закрытие вентиля.

6. Передаточная функция Объекта Управления.

Вывод передаточной функции для рабочей ёмкости, в

которой регулируется уровень жидкости.

Предварительно получим дифференциальное уравнение для рабочей

емкости и затем выражение для передаточной функции.

Регулируемая величина − уровень жидкости в емкости h₁, регулирующее

воздействие − изменение проходного сечения вентиля f₁, возмущающие

воздействия − изменения h₀, G, m₁ и m₂.

Основными уравнениями, описывающими изменение уровня жидкости в

емкости, являются:

1. Уравнение материального баланса

(1)

где ΔV- приращение объема жидкости в емкости за время Δt ;

- объемная подача жидкости в рабочую емкость в единицу времени;

- объемный унос жидкости из рабочей емкости в единицу времени;

При вертикальных стенках емкости

(2)

где S– площадь «зеркала» жидкости;

Δh₁ - приращение уровня жидкости за время .

Подставляя (1) в (2) и переходя к бесконечно малым приращениям dh₁ и

d t, получим

(3)

2. Уравнение расхода при истечении жидкости через вентиль f1

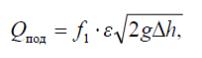( 4)

где f₁ – площадь проходного сечения вентиля, м²;

ε - коэффициент расхода, учитывающий влияние местных сопротивлений в данной работе ε = 0,60 - 0,65;

g – ускорение силы тяжести;

Δh = h₀ – h₁ – перепад уровней жидкости в емкостях.

3. Уравнение уноса жидкости тканью из рабочей емкости

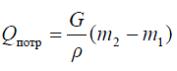(5)

где G – массовый расход ткани, г/с;

ρ – плотность жидкости, г/л;

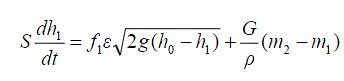m₁, m₂ – абсолютная влажность ткани соответственно на входе и выходе плюсовки, г/г;

Подставляя (5) и (4) в (3), получим уравнение объекта регулирования

₍₆₎

Здесь регулируемая величина – h₁, регулирующее воздействие –

изменение f₁, возмущающие воздействия – изменение h₀, G, m₁, m₂.

Уравнение (6) нелинейное. Выполним его линеаризацию.

Запишем уравнение (6) в следующем виде

Р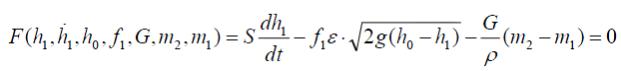 азложим функцию F в ряд Тейлора по отклонениям переменных

величин от номинального режима:

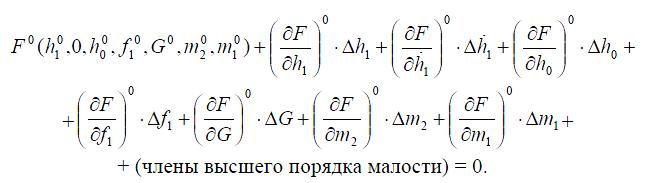
Вычтем из этого уравнения выражение для установившегося движения F0,

и, пренебрегая малыми величинами высшего порядка, получим

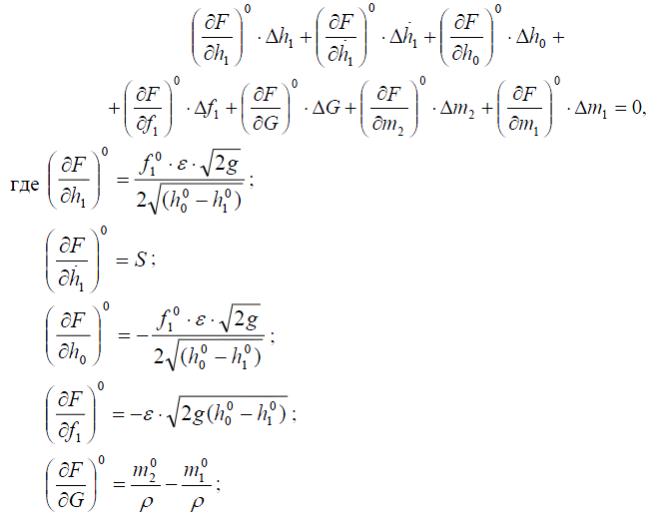
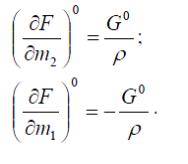
Таким образом, линеаризованное дифференциальное уравнение (6) в

отклонениях запишется:

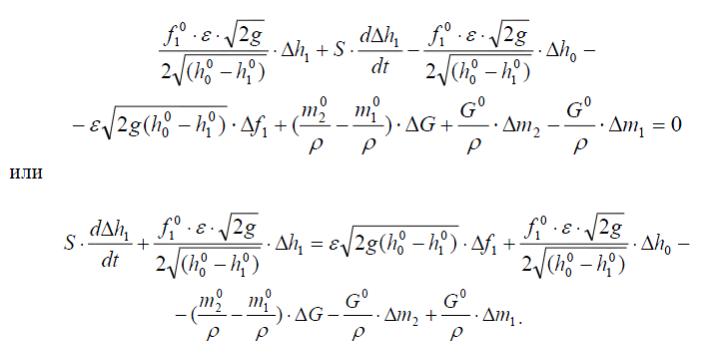_{(7) Введем обозначения:}

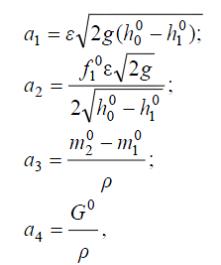
где , , , , , G⁰– значения соответствующих параметров при номинальном режиме работы системы, кроме того, для малых отклонений Δh₁, Δf₁, Δh₀, ΔG, Δm₂ и Δm₁ примем обозначения h₁, f₁, m₁, m₂, G.

С учетом обозначений уравнение (7) принимает вид

(8)

Приведя уравнение (8) к стандартному виду (разделив правую и левую

части на a₂), получим

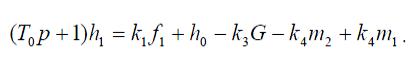₍₉₎

_{Здесь T0 = S/a2 – постоянная времени объекта;}

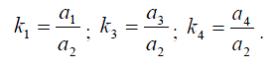
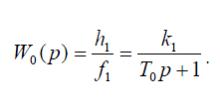
Уравнение (9) позволяет записать передаточную функцию для рабочей ёмкости

Все параметры, необходимые для вычисления постоянной времени и

к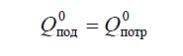 оэффициентов передачи объекта, приведены в задании. Не указано лишь номинальное сечение вентиля , которое необходимо определить из уравнения равновесного режима:

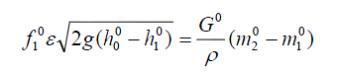и ли