22.The aerodynamic characteristics of a aerodynamic profile in a subsonic compressed flow at Mach numbers smaller then critical value.

The flow over bodies at supersonic speeds is very different from that at subsonic speeds. As discussed earlier, the differential equations for inviscid flow become hyperbolic, rather than elliptic as the Mach number exceeds 1.0.

The angle of the waves generated when the disturbances are small is called the Mach angle:

Sin β = a dt / V dt = 1/M

The Mach wave is a boundary between areas that are affected by the presence of very small disturbances and those that are unaffected. A shock wave, however, is produced by larger disturbances. As the flow is compressed, the temperature changes, the speed of sound changes, and the shock angle becomes greater than the Mach angle.

The important point here is that there are two solutions, one corresponding to weak shock waves and one corresponding to strong shocks. The weak shock solution is the one that actually occurs in most external aerodynamics problems. This solution has a maximum value of δ and θ for any incident Mach number. This means that there is a maximum value of turning angle that is possible.

When the flow is forced to turn a corner, a shock wave is created.

Subsonic aircraft such as the Supermarine Spitfire, BF 109, P-51 Mustang, Gloster Meteor, He 162, P-80 have relatively thick, unswept wings and are incapable of reaching Mach 1.0. In 1947, Chuck Yeager flew the Bell X-1 to Mach 1.0 and beyond, and the sound barrier was finally broken.

23.The aerodynamic characteristics of a finite-span wing in a subsonic compressed flow at Mach numbers smaller then critical value.

Aerodynamic forces acting on finite span wing at subsonic speeds in the presence of heat transfer are investigated using the momentum conservation law for a continuous medium. An analytical expression for the principal vector of aerodynamic forces in view of heat transfer is obtained. The expression allows the effect of heat transfer on the bearing properties of the wing to be investigated. The numerical simulation results of the aerodynamic characteristics of finite span wings that have been obtained with commercial software in solving the Navier−Stokes equations are presented, which completely confirm the results of the analytical studies of the effect of heat transfer on the lift. An analytical estimate of the lift of a flat plate at a zero angle of attack when heating or cooling one of the streamlined surfaces was done.

24.Critical Mach number of an aerofoil section and its relation to the geometrical characteristics and angle of attack of an aerofoil section.

The pressure on the surface of the airfoil is thus:

Note that θ is positive when the flow is being turned away from the freestream direction, and negative when it is being turned back.

Since the same solution applies all along the characteristic line, this is the pressure in the flow field as well, with changes due to dispersion and dissipation.

Unlike the incompressible case, we require supersonic airfoils to produce small perturbations if they are to satisfy the equations. This means small surface slopes everywhere: no blunt leading edges. This means that we can express the surface slope as:

Note that the Cp equations are linear in θ, thus the net Cp is the sum of that due to thickness, camber, and angle of attack. T he net lift and moment is then also the sum of those associated with each of the 3 components. Note that the flat plate at angle of attack is the only component that contributes to the integral.

The result for any supersonic airfoil is then:

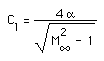(The zero lift angle of attack is always 0)