1.9.1. Операции соединения

В принципе, операции соединение двух или нескольких систем — во многом сходны со способами соединения элементов в электрических цепях, т.е. это достаточно простые операции. Как правило, требуется лишь соединить выход одной системы с входом другой или подать один и тот же входной сигнал на входы двух систем. Поэтому процедура соединения, в некотором смысле, аналогична, например, процедуре разработки общей принципиальной схемы сложного электротехнического устройства, состоящего из отдельных элементов, модулей или блоков.

В общем случае, для того чтобы соединить между собой две системы нужно разбить их множества входов и выходов на определенные системы подмножеств, а именно: во множествах входов и выходов следует выделить группы подмножества подлежащих и не подлежащих соединению.

Введем понятие соединяемых систем. Пусть — общая система с входным объектом и выходным - . Здесь и - компонентные множества.

В общем случае не все, а только некоторые компонентные множества входов или выходов могут служить для реализации соединений. Обозначим через семейство компонентных множеств , которые не участвуют в соединении

,

а через — декартово произведение множеств из ,

.

Обозначим через декартово произведение входных компонентных множеств, участвующих в соединении.

Таким образом, входной объект системы можно представить как произведение двух составных компонент:

.

Поступая аналогичным образом в отношении выхода системы, обозначим через декартово произведение выходных компонент, которые могут участвовать в соединении, а через - декартово произведение выходных компонент, которые не участвуют в соединении. Тогда выход системы можно представить в виде

.

Теперь для каждой такой системы можно образовать, вообще говоря, некоторое счетное множество соединяемых систем

,

которые отличаются друг от друга выбором и , а также типом соединения. Таким образом, связь между системами определенными над и , и системами , определенными над и , заключается в следующем. Оба приведенные случаи по существу - одинаковые системы, которые отличаются одна от другой только типами соединений.

Под соединяемыми системами будем понимать множество

.

Рассмотрим элементарные типы соединений систем и установим соответствующие операции соединения.

Каскадное соединение систем.

Зададим отображение такое, что , если

, , ,

и

.

Э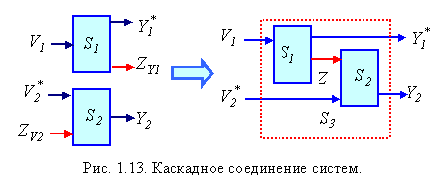 то отображение « » будем называть операцией каскадного соединения или каскадной соединяющей операцией.

Параллельное соединение систем.

Определим отображение такое, что , если

, , то , и .

Т огда отображение «+» будем называть операцией параллельного соединения, или параллельной соединяющей операцией.

Замыкание обратной связи.

Пусть отображение , такое, что , где

, ,

и .

Т огда отображение называется замыканием обратной связи или операцией замыкания обратной связи.

Схематическое изображение операций соединения приведено на рисунках 1.13.-1.15. Следует отметить, что эти операции можно было бы определить и другими способами. Например, вместо того, чтобы определять замыкание обратной связи для одиночной системы и соединять ее выход с входом, как показано, на рис. 1.15.а), можно было бы предположить, что в цепи обратной связи должна быть еще одна подсистема, как показано на рис. 1.15.б). Однако три основные операции, введенные выше, исчерпывают в различных комбинациях большинство интересных случаев, и в этом смысле их можно рассматривать как примитивные. Например, соединение, изображенное на рис. 1.15.б), как следует из рис. 1.13, можно представить в виде (см. рис. 1.15.б).

Рассмотрим реализацию операций соединения на примере двух систем «высшее учебное заведение» - ВУЗ, и «приемная комиссия» -Пк. Вход системы Пк состоит из следующих компонентных множеств: - множество абитуриентов сдавших документы в приемную комиссию, - множество отчисленных студентов, желающих восстановиться на соответствующий курс, и - множество студентов других вузов, желающих обучаться в данном ВУЗе по переводу, т.е. . Выход системы Пк – компонентное множество, состоящее из подмножеств: - множество абитуриентов сдавших успешно вступительные экзамены, - множество абитуриентов не сдавших вступительные экзамены, - множество студентов зачисленных в ВУЗ и - множество студентов, которым отказано в приеме. Множество в свою очередь состоит из двух подмножеств: - множества абитуриентов у которых сумма балов меньше проходного и - множества абитуриентов у которых сумма балов больше проходного балла. Эти множества находятся в отношении порядка, так как у абитуриентов множества сумма баллов меньше, чем у абитуриентов принадлежащих , т.е. . Разобьем множество выходов системы Пк на два подмножества: не подлежащее соединению (на его подмножествах выполняется отношение эквивалентности – «не принятые в ВУЗ») и подлежащее соединению (на его подмножествах также выполняется отношение эквивалентности – «зачислены в ВУЗ»). Множество входов системы ВУЗ совпадает по своей структуре с множеством , обозначим его . Множество выходов состоит из двух подмножеств: - множества студентов отчисленных с первого курса, - множества студентов отчисленных с других курсов, имеющих незаконченное высшее образование, и - множество выпускников ВУЗа, имеющих законченное высшее образование, т.е. . Таким образом, для рассматриваемых систем, получим, что и .

О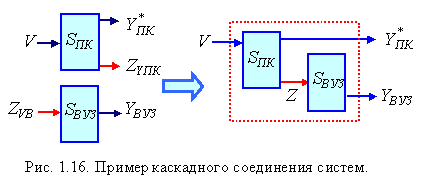 чевидно, что эти две системы могут быть соединены каскадно, в результате получим и .