1.7. Временные системы

Для того чтобы в рамках системного анализа исследовать эволюцию систем во времени, необходимо определить понятие времени в виде такого абстрактного объекта, который наиболее полно отражал бы самые существенные черты интуитивных представлений человека о времени.

Множеством моментов времени (временной системы) будем называть линейно упорядоченное множество, для любых двух элементов которого имеет место отношение линейного порядка. Для дальнейшего будем считать, что в множестве содержится минимальный элемент , такой что .

Пусть и некоторые произвольные множества. Обозначим через и множества всех возможных отображений из в и соответственно, т.е.

.

Временной системой над множествами и будем называть подмножество

при этом множества и называют временными объектами системы. Элементы этих множеств и называют абстрактными функциями времени. Значения этих функций в момент времени обозначают и .

Р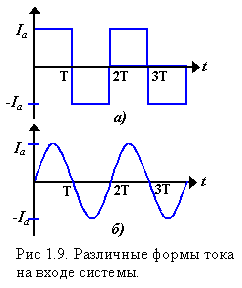 ассматриваемая система «выпрямитель тока» - временная система. Пусть на вход системы подается периодический ток прямоугольной формы (рис. 1.9.а.) с полупериодом равным и амплитудой . Для того чтобы описать систему «выпрямитель тока», как временную, зададим множество значений тока и множество моментов времени в виде множества натуральных чисел, т.е. . Определим временные объекты, как отображения и . Для этого необходимо поставить в соответствие элементам множества - натуральным числам, элементы множества . Как следует из рис. 1.9.а., для элементов множества четным значениям соответствует значение тока , а нечетным - . Тогда для определения элементов получим соотношение

.

График этого отображения приведен на рис. 1.10. Поскольку на выходе направление тока неизменно, то . Таким образом, временная система будет состоять из элементов

.

Рассмотрим случай, когда на вход системы подается ток, изменяющийся по гармоническому закону. В этом случае множество - непрерывно и равно множеству действительных чисел. При этом, элементом множества является непрерывная функция времени . Для того чтобы определить временной объект , воспользуемся функцией

.

Тогда . Исходя этих соотношений для временной системы «выпрямитель тока» получим, что связь между выходом и входом такой системы определяется соотношением

. (1.5.)

График функции выхода системы приведен на рис 1.11.

И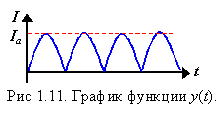 з рассмотренного примера следует, что существует, по крайней мере, два класса временных систем: дискретные системы, для описания которых используются дискретные множества входов и выходов и системы с непрерывными множествами входов и выходов. Дискретные системы рассматриваются в рамках теории автоматов, а непрерывные системы – в рамках теории динамических систем. Для того чтобы перейти к более конкретному описанию системы различных типов, необходимо ввести новые вспомогательные объекты, которые называются объектами состояний, а их элементы - состояниями системы.