1.6. Теоретико-множественное определение системы. Модель «черного ящика»

Основные принципы построения теории систем, заключаются в следующем.

1. Основные понятия теории систем вводятся с помощью формализации. Это значит, что исходя из словесного описания интуитивного понятия системы, дается точное математическое определение.

2. Исходя из основных понятий, полученных в результате формализации, излагаются математические методы системного анализа необходимые для исследования систем.

Понятие системы определяется как некоторое отношение на языке теории множеств.

Пусть задано семейство непустых абстрактных множеств

где - множество индексов, а множества - компоненты системы.

Системой называется отношение на непустых, абстрактных множествах

(1.1)

где - операция декартового произведения множеств. Множество будем называть объектом системы. Если множество конечно, то (1.1) можно переписать в виде

. (1.2)

Другими словами, под системой, заданной на , будем понимать некоторое собственное подмножество декартового произведения :

или

Пусть подмножества и образуют разбиение множества на два подмножества, таких что и . Множество будем называть входным объектом или множеством входов системы, а множество - выходным объектом, или множеством выходов системы. Тогда система определяется отношением

(1.3)

Если является функцией

, (1.4)

т.е. система определяется как отображение множества входов на множество выходов, то соответствующая система будет называться функциональной.

В определении системы с помощью соотношения (1.3) не содержатся объекты, описывающие внутреннее устройство системы. Поэтому ее можно изобразить в виде "черного ящика", выделенного из окружающей среды. Подчеркнем, что уже эта, максимально простая, модель отражает два важных свойства системы: целостность и обособленность от среды.

Д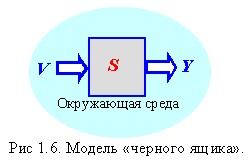 алее, из определения (1.3.) косвенно следует, что хотя "ящик" и обособлен, выделен из среды, он не является полностью от нее изолированным. Результаты деятельности системы, как правило, приводят к заранее известным изменениям в окружающей среде, т.е. система воздействует на среду. Такого типа воздействие на внешнюю среду и называют выходом системы.

В определении имеется указание и на наличие связей другого типа, которые отражают влияние окружающей среды на систему, т.е. такие связи со средой, которые направлены извне в систему. Они называются входами системы.

Систему определенную таким образом, называют моделью черного ящика, чем образно подчеркивается полное отсутствие информации о внутреннем устройстве системы. В рамках этой модели исследуются возможные отношения между входами и выходами системы. Такая модель, несмотря на ее внешнюю простоту и на отсутствие сведений о структуре системы, оказывается полезной, а часто и единственно возможной, на начальном этапе исследования сложных систем.

Приведенные определения системы являются наиболее общими. Действительно, если некоторая система задается какими-то более конкретными математическими конструкциями, скажем системой линейных уравнений, то, очевидно, что эти уравнения одновременно либо определяют некоторое отношение, соответствующее определению (1.1), либо являются его следствием. Например, такая система, как электрическая цепь с сосредоточенными параметрами описывается системой линейных уравнений, которые порождаются двумя типами отношений эквивалентности:

• сумма токов в узлах цепи равна нулю;

• сумма падений напряжений на участках замкнутого контура равна сумме действующих ЭДС.

Естественно что, различным системам соответствуют и различные способы описания, но все они могут быть сведены к отношению вида (1.1).

С уществует обширный класс, так называемых «нечетких систем» (примерами таких систем могут служить системы распознавания образов, экспертные системы и системы искусственного интеллекта), когда систему удается описать лишь словесно на качественном уровне. Тем не менее, все эти словесные утверждения в силу их лингвистических функций будут подпадать под отношение типа (1.1). Действительно, каждое высказывание содержит две основные лингвистические категории: денотаты и функторы, причем денотаты используются для обозначения объектов, а функторы для обозначения отношения между ними. И для каждого правильного множества словесных утверждений существует отношение (в математическом смысле этого слова), описывающее формальную взаимосвязь между объектами, обозначаемыми денотатами (это отношение называется моделью этих утверждений). Таким образом, система, в общем случае, всегда является отношением в смысле (1.1), а уже более узкие классы систем определяются более точно своими специфическими средствами, будь они лингвистическими, математическими, программными или какими-то другими.

Следует отметить, что практически всегда, исходя из модели «черного ящика» для исследуемой системы можно получить данные о ее структуре. Предположим, что необходимо разработать систему, на вход которой подается переменный ток (т.е. направление тока изменяется), который на выходе преобразуется в постоянный ток (направление тока неизменно).

Проведем предварительное рассмотрение задачи. Пусть множество входов (входных зажимов) системы - , а множество выходов (выходных зажимов) - .

Введем в рассмотрение отношение - «направление тока» такое, что для пары (кортежа) ток направлен от к . С учетом этого отношения построим допустимые множества входов и выходов исследуемой системы. Для этого вычислим декартовы произведения

,

.

Тогда множества допустимых входов и выходов, удовлетворяющие заданным условиям, будут иметь вид:

, .

С учетом этих множеств будем иметь

.

Такая модель системы носит пока что исключительно описательный характер (по существу это переформулированное условие задачи исследования).

После этапа предварительного анализа можно установить структуру системы. Для этого немного переформулируем задачу, а именно: установим, как должны соединяться входы и выходы системы, чтобы обеспечить неизменность направления тока на выходных зажимах. Для этого, нужно ввести в рассмотрение новое отношение. Будем называть отношение «порядком соединения»

или .

Кортеж вида указывает, что элемент соединяется с и т.д. Для того чтобы установить порядок соединения входных и выходных элементов исследуемой системы воспользуемся отношением:

Поскольку операция декартового произведения ассоциативна, то это отношение можно переписать в виде

Соответственно, для рассматриваемой системы

в этом случае получим

.

И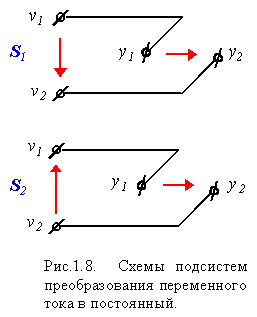 з последнего соотношения следует, что система состоит из двух подсистем: и . Связи между входами и выходами этих подсистем можно изобразить в виде схем, как на рис. 1.8.

Следует отметить, что рассмотренная процедура выделения подсистем из исходной системы, в системном анализе называется процедурой декомпозиции системы. Очевидно, что в данном случае установление структуры системы недостаточно для полноты описания ее поведения или функционирования. Это связано с тем, что в рамках рассмотренной модели не учитывается такой объект как время.