1.10. Нечеткие системы

Пытаясь формализовать человеческие знания, исследователи постоянно сталкиваются с целым рядом проблем. Существует класс явлений, процессов и объектов, для описания которых используются преимущественно качественные характеристики (мало, много, сильный, слабый и т.д.). Эти характеристики обычно размыты (нечеткие) и не могут однозначно интерпретироваться, однако содержат важную информацию. Например, «Одним из возможных признаков гриппа является высокая температура». Это очень осложняет, а чаще всего делает невозможным использование традиционного математического аппарата для их описания. Не исключено, что системы с нечеткими характеристиками можно было - бы описать в рамках классической теории множеств. Однако здесь есть одно принципиальное препятствие, которое содержится в самом определении множества. Для заданного множества и некоторого объекта может выполняться только одно из двух соотношений: либо , либо . При этом само множество можно рассматривать как совокупность эквивалентных элементов (некоторый класс эквивалентности), эквивалентных в том смысле, что все они обладают одинаковым свойством: принадлежат множеству .

Попытаемся теперь составить множество элементы которого – расстояния соответствующие субъективному понятию «близко». В рамках классического подхода такое множество определим следующим образом. Будем считать, что все расстояния меньшие либо равные 1000 м. – это расстояния соответствующие понятию «близко». Таким образом . Однако, у разных людей понятию «близко» соответствуют разные предельные значения таких расстояний. Например, для одной группы людей «близко» - это расстояние до 800 м., для другой группы – до 1500 и т.д. Отсюда следует, что множество , строго говоря, не имеет четкой границы, следовательно, в одном случае может принадлежать множеству , а в другом – нет. При этом элементы множества уже не эквивалентны между собой, так как нельзя однозначно определить их принадлежность данному множеству. Кроме того, с этим понятием связаны еще и определенные градации «очень близко», «не очень близко», «не далеко». Таким образом, в рамках классической теории множеств не удается описать подобные объекты, сохранив при этом нечеткость (расплывчатость) их характеристик.

1.10.1. Нечеткие множества.

В 1965 г. американский математик Л. Заде опубликовал статью под названием «Fuzzy sets», что можно перевести как «Нечеткие множества». В статье дано новое определение понятия множества, предназначенное для описания и исследования сложных, «плохо определенных», «нечетких» систем. В этих системах наряду со строгими, объективными, количественными данными и результатами присутствуют неоднозначные субъективные, качественные данные.

Нечеткость – это такое свойство объектов или явлений, при котором не выполняется отношение эквивалентности: объект одновременно может принадлежать данному множеству и не принадлежать ему. Неопределенность такого типа описывается с помощью функции принадлежности; значение этой функции выражает степень уверенности, с которой мы относим данный объект к указанному множеству. Само множество в итоге становится не определяемым однозначно и называется нечетким множеством.

Новый математический аппарат, основанный на нечетких множествах, используется для описания свойств нечетких систем. Изложим основные понятия теории нечетких множеств.

Носитель – это универсальное множество, к которому относятся все результаты наблюдений, исследований некоторого абстрактного или реального явления, объекта или процесса. Например, если предметом исследования является возраст занятых в определенных отраслях экономики, то носитель – это отрезок вещественной оси =[16, 75], при условии что возраст человека измеряется в годах. Можно сказать что нечеткое множество А – это некоторое подмножество носителя . Оно состоит из неопределенного числа элементов : признаки, по которым элементы включаются в нечеткое множество, не позволяют однозначно отделить все элементы, которые в него входят, от элементов множества U, ему не принадлежащих. О принадлежности некоторого множеству А, можно говорить только с определенной степенью условности, или по другому, для элементов можно задать некоторую количественную характеристику, которая определяет степень принадлежности элемента множеству А. Эту количественную характеристику называют функцией принадлежности нечеткого множества А, и обозначают . Естественно считать что, если для некоторого функция , то этот элемент однозначно принадлежит множеству А. В случае, когда - однозначно не принадлежит множеству А.

В общем случае, что для каждого элемента можно задать такое число , , которое выражает степень принадлежности этого элемента нечеткому множеству . Таким образом, для функции принадлежности областью определения является носитель , а областью значений – промежуток .

Если принимает значения либо только 0, либо только 1, то множество является, как принято говорить, «жестким» (классическим) множеством. Характерным признаком нечеткости множества является наличие хотя бы одного элемента с функцией принадлежности, отличной от 0 и 1. Причем чем больше значение функции принадлежности, тем с большей уверенностью можно отнести данный элемент к множеству А.

Нечеткое множество заданное на носителе – это множество пар вида , т. е. ), где - функция, принимающая значения из промежутка [0, 1], .

С нечетким множеством тесно связано понятие лингвистической переменной, впервые введенное Л. Заде. Это основной тип переменных, которые используются в естественных языках при составлении описания моделей систем (лингвистических моделей). Лингвистическая переменная определятся следующим образом:

,

где - значения лингвистической переменной, – терм-множество значений, т.е. совокупность ее лингвистических значений, – носитель, – синтаксическое правило, порождающее термы множества , – семантическое правило, которое каждому лингвистическому значению  ставит в соответствие его смысл , причем определяет нечеткое подмножество носителя . Множество - называют еще базовой шкалой лингвистической переменной.

Рассмотрим описание лингвистической переменной на следующем примере. Зададим лингвистическую переменную с названием «Возраст работника» с лингвистическими значениями: =«Оптимальный» и =«Не оптимальный». Определим синтаксическое правило как «оптимальный возраст для работы в промышленности», налагаемое на переменную . Тогда полное терм-множество значений может состоять из двух элементов: =«Оптимальный возраст работника» и =«Неоптимальный возраст работника». Носитель - это промежуток , который содержит все возможные значения возрастов работников. На этом носителе определены две функции принадлежности: для терма - нечеткое множество с функцией принадлежности и для - нечеткое множество с функцией принадлежности . Если, по мнению экспертов, оптимальный возраст работника для промышленности – около 40 лет, то семантические правила могут иметь вид: = «Если возраст работника около 40 лет, то это оптимальный возраст для работников промышленности» и = «Если возраст работника сильно отличается от 40 лет, то это не оптимальный возраст для работников промышленности». Исходя из этого можно установить вид функций принадлежности для множеств и , их графики приведены на следующем рисунке.

Функция принадлежности может быть задана аналитически или таблично. Рассмотрим простейшие примеры использования нечетких множеств и способы задания функции принадлежности.

Определим с помощью нечеткого множества понятие «несколько». Для этого необходимо из базовой шкалы, множества натуральных чисел , выделить некоторое нечеткое подмножество чисел , которое соответствует нашему субъективному представлению об этом понятии. Зададим функцию принадлежности множества в виде таблицы.

	1	2	3	4	5	6	7	8	9	10
	0	0,1	0,6	0,8	1	1	0,9	0,7	0,2	0

Значения функции принадлежности можно интерпретировать следующим образом: число 2 на 10% принадлежит множеству , или на 10% процентов соответствует интуитивному понятию «несколько». Аналогичным образом можно ввести нечеткие множества, соответствующие понятиям «много», «мало», «около 50», «почти 20». Приведем примеры нечетких множеств, функция принадлежности которых задается аналитически. Предположим, что из множества действительных чисел необходимо выделить нечеткое подмножество , которое соответствует интуитивному понятию «около 50». Поскольку множества и - непрерывные, то функцию принадлежности лучше всего задать аналитически. Очевидно, что эта функция должна стремиться к единице при , и к нулю - при . Поэтому для задания воспользуемся формулой аналогичной для плотности вероятности нормального распределения

.

З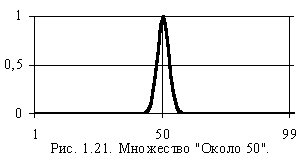 десь - среднее значение случайной величины, а - дисперсия. Будем считать, что понятию «около 50» примерно соответствуют числа из диапазона (45,55). Тогда чтобы построить функцию принадлежности положим = 50, а = 4,5. В результате получим

.

На рис. 1.21. приведен график .

Рассмотрим еще один пример аналитического задания функции принадлежности. Введем лингвистическую переменную «возраст». Ее базовый набор значений – «младенческий», «детский», «юношеский», «молодой», «зрелый», и «старый». Базовой шкалой для этой лингвистической переменной, в общем случае, является множество действительных чисел из интервала (0, 130), . Выделим из множества нечеткое подмножество старых людей . Пусть в результате опроса экспертов было установлено, что возраст 50 лет является переходным между зрелостью и старостью. Тогда функцию принадлежности , можно задать следующим образом:

З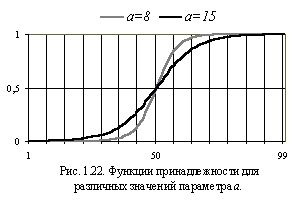 десь переменная - это параметр, учитывающий субъективность оценки возраста («размытости» нечеткого множества): чем больше этот параметр тем более «размытым» будет множество (см. рис. 1.22.).

Пустое нечеткое множество определяется как такое, для которого .

Равенство двух нечетких множеств и определяется следующим образом. Два нечетких множества и равны тогда и только тогда, когда равны их функции принадлежности для всех . Это утверждение можно записать в более компактном виде:

.

Включение нечеткого множества в множество определяется следующим образом: .

Например, множество долгожителей является подмножеством старых людей.

Нечеткое множество называется номинальным тогда и только тогда, когда , в противном случае – субнормальным. Непустое субнормальное множество можно нормализовать, т.е. преобразовать его к номинальному нечеткому множеству, разделив на .

Например, нечеткое множество старых людей - номинальное множество, так как точная верхняя грань его функции принадлежности равна единице:

Рассмотрим основные операции на нечетких множествах. Часть этих операций обозначается точно так же как и в случае классических, четких множеств. Помимо этого операциям на нечетких множествах приписывается лингвистическое толкование.

Объединение нечетких множеств.

О бъединением нечетких множеств и называется множество функция принадлежности которого равна . Этой операции соответствует высказывание « ». Приведенное высказывание раскрывает лингвистический смысл данной операции применительно к нечетким множествам. Например, объединением множеств «Около 50» и «Около 57» будет множество «Около 50 или 57». График функции принадлежности этого множества приведен на рис. 1.23.

Пересечение нечетких множеств.

П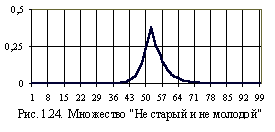 ересечением нечетких множеств и называется множество функция принадлежности которого равна . Этой операции соответствует высказывание « », раскрывающее ее лингвистическое содержание. Например, для множеств «Старый» и «Не старый» пересечением будет множество «Не старый и не молодой». График функции этого множества имеет вид (см. рис. 1.24.).

Отметим, что поскольку функция принадлежности данного множества принимает значения меньшие единицы, то оно является субнормальным. Для данного множества . Разделив на это число, преобразуем данное множество к номинальному. На рис 1.25. приведен график функции принадлежности нормализованного множества.

Дополнение.

Д ополнением нечеткого множеств до множества называется множество функция принадлежности которого равна . Лингвистический смысл этой операции определяется высказыванием « ». Например, для множества «Старый» дополнением является множество «Не старый». График функции принадлежности этого множества приведен на рис. 1.26.

Концентрация.

Для нечеткого множества концентрацией является множество функция принадлежности которого определяется из соотношения

.

Лингвистический смысл этой операции заключается в следующем. Например, для лингвистической переменной «старый», концентрация соответствует высказыванию «очень старый». На рис. 1.27. приведены графики функций принадлежности нечеткого множества «старый» и его концентрации «очень старый».

Размывание.

Размыванием нечеткого множества называется множество функция принадлежности которого определяется из соотношения

.

Л ингвистический смысл этой операции – «не очень». Например, для лингвистической переменной «старый» размывание – это «не очень старый». На рис. 1.28. приведены графики функций принадлежности для нечетких множеств «старый» и его размывания «не очень старый».

Последние две операции применимы только к нечетким множествам.

Декартовым произведением нечетких множеств заданных на универсальных множествах соответственно нечеткое подмножество декартового произведения  с функцией принадлежности вида