
- •Задачи компьютерной графики и ее место среди других методов обработки информации
- •Основные направления компьютерной графики. Основные структурные элементы системы машинной графики
- •Виды данных, представленных в форме изображений
- •Класс 1: тоновые и цветные изображения
- •Класс 2: двухуровневые или представляемые в нескольких «цветах» изображения
- •Класс 3: непрерывные кривые и линии
- •Класс 4: точки или многоугольники
- •Виды данных, представленных в форме изображений Понятие изображения
- •Понятие о структуре изображения. Основные графические элементы (примитивы)
- •Графические элементы (примитивы).
- •Видимые и невидимые поверхности. Ограничения на сложность изображения
- •Ограничения на сложность изображения
- •Тесты глубины Тест 1.
- •Тест 2.
- •Тест 3. Проверка сканирующей прямой
- •Алгоритмы удаления невидимых поверхностей
- •Алгоритм сканирующей прямой Уоткинса
- •Алгоритм Робертса
- •Растровое представление геометрических объектов. Растровая развертка отрезка
- •Растровая развертка отрезка.
- •Растровая развертка сплошных областей. Закраска многоугольников
- •Закраска многоугольников.
- •Растровая развертка сплошных областей. Закраска ограниченной области
- •Алгоритмы отсечения отрезков Отсечение отрезков
- •Алгоритм Сазерленда-Коэна
- •Алгоритм средней точки
- •Алгоритм Кируса-Бека
- •Метод Гуро
- •Метод Фонга
- •Модели расчета освещенности граней трехмерных объектов
- •Методы трассировки лучей. Метод прямой трассировки лучей
- •Классический метод обратной трассировки лучей
- •Методы повышения качества изображения при обратной трассировке лучей Текстурные карты и свойства материалов. Работа с растровыми картами (bmp, png, jpeg)
- •Отображение шероховатости (bump-mapping)
- •Сглаживание (antialiasing)
- •Кубические сплайны
Ограничения на сложность изображения
1. Контур, ограничивающий поверхность аппроксимируется ломаной линией. Тогда хранятся и преобразуются только точки, являющиеся координатами вершин ломаной линии. Остальные точки контура восстанавливаются после проведения всех геометрических преобразований с координатами вершин.
2. Все изображаемые поверхности являются плоскими. Следовательно, изображаемое тело является многогранником, в общем случае произвольной формы. Тогда возможно применение быстрой тоновой заливки плоских граней специальными алгоритмами, т.к. тон не изменяется в пределах отдельной грани. Тон заливки изменяется только от грани к грани в соответствии с положением источника освещенности и удаленности от него.
3. Изображаемые тела являются выпуклыми. Тогда плоская грань невидима, если нормаль к ней образует угол больший 90o с направлением к точке зрения. Тогда объект сложной формы представляется объединениями его выпуклых частей, у которых из рассмотрения сразу исключены все задние, т.е. невидимые грани.
Напомним, что плоский многоугольник является выпуклым, если через каждое его ребро можно провести прямую так, что все вершины многоугольника, не находящиеся на этой прямой, окажутся по одну сторону от нее (окажутся в одной плоскости).
Напомним также, что двумерная проекция выпуклого трехмерного многоугольника так же является выпуклым плоским многоугольником.
После удаления невидимых поверхностей в данной структуре появляется указание о видимости каждой ее вершины.
Если некоторая вершина в этой структуре полностью невидима, то невидимы и все ее вершины нижних уровней.
На самом нижнем уровне число точек ребра и их координаты могут меняться в зависимости от текущего положения изображаемых объектов.
Тесты пересечения на плоскости
Пересечение двух прямых на плоскости
Пусть плоскости заданны уравнениями:

определяется как решение матричного уравнения:

Если
 ,то
прямые параллельны. Дополнительное
условие
,то
прямые параллельны. Дополнительное
условие
![]() определяет
совпадают ли параллельные прямые или
нет. В противном случае точка пересечения
определяется как:
определяет
совпадают ли параллельные прямые или
нет. В противном случае точка пересечения
определяется как:
![]()
Пересечение двух отрезков в плоскости
Пусть заданы две прямые, пересекающиеся
в точке
![]() . На
каждой из них своими начальной и конечной
точками заданы отрезки
. На
каждой из них своими начальной и конечной
точками заданы отрезки
![]() ,
где
,
где
![]()
Тогда два отрезка пересекаются в , если:
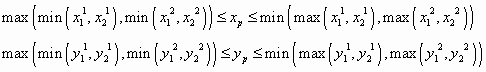
Пересечение плоскости и прямой
Плоскость задана уравнением
![]() ,
где
,
где
![]() -
вектор, перпендикулярный заданной
плоскости (направляющий вектор) длины
-
вектор, перпендикулярный заданной
плоскости (направляющий вектор) длины
![]() ,
а D - смещение плоскости от начала
координат, где
,
а D - смещение плоскости от начала
координат, где
![]() -
расстояние плоскости от начала координат.
-
расстояние плоскости от начала координат.
Уравнение плоскости описывает множество ее точек с координатами (x;y;z). Перепишем его в нормированном виде:
![]()
Если D = 0, то заданная плоскость
проходит через начало координат, а ее
уравнение называется уравнением
плоскости без смещения. Фактически
плоскость может быть представлена
множеством векторов, проведенных их
начала координат в точки
![]() ,
перпендикулярных направляющему вектору
плоскости
.
Другими словами, это векторы, расстояние
от которых до заданной плоскости равно
нулю. Это утверждение можно записать
как:
,
перпендикулярных направляющему вектору
плоскости
.
Другими словами, это векторы, расстояние
от которых до заданной плоскости равно
нулю. Это утверждение можно записать
как:

Заметим, что
![]() .
.
С другой стороны, прямая, проходящая
через две точки
![]() имеет
длину
имеет
длину ![]() .
Ее проекция на ось Х имеет длину
.
Ее проекция на ось Х имеет длину
![]() ,
и определяется направляющим углом
,
и определяется направляющим углом
![]() относительно
оси ОХ. Аналогично
относительно
оси ОХ. Аналогично
![]() . Тогда
значения
. Тогда
значения
![]() представляют
собой проекции единичного направляющего
вектора прямой на оси координат.
представляют
собой проекции единичного направляющего
вектора прямой на оси координат.
Расстояние точки
![]() до
плоскости есть величина
до
плоскости есть величина
![]() с
учетом расстояния
с
учетом расстояния
![]() до
самой плоскости от начала координат.
Тогда длина r от точки
до
точки пересечения с плоскостью
до
самой плоскости от начала координат.
Тогда длина r от точки
до
точки пересечения с плоскостью
![]() есть
величина, полученная из соотношения:
есть
величина, полученная из соотношения:
![]()
Величина
![]() определяется
как угол между направляющим вектором
прямой и нормалью к плоскости.
определяется
как угол между направляющим вектором
прямой и нормалью к плоскости.

Тогда
![]()
Координаты точки пересечения прямой с плоскостью определяется из соотношений:



Тесты принадлежности. Тест видимости
Тесты принадлежности.
Эти тесты проверяют, лежит ли точка Р
внутри плоского многоугольника
![]() .
.
Тест 1.
Пусть ai - угол между
отрезками PiPi+1
и Pi+1Pi+2. Тогда
точка P находится вне многоугольника
F, если
![]() и
внутри, если
и
внутри, если
![]()

Рисунок 10.1. Тест принадлежности 1
Тест 2.
Пусть R - луч из точки Р, проходящий через F, но не содержащий ни одной его вершин Pi. Тогда, если число пересечений F и R нечетно, то Р внутри многоугольника, а если четно, то Р находится снаружи.

Рисунок 10.2. Тест принадлежности 2
Тест видимости
Этот тест применяется к трехмерным телам. С помощью него выявляются задние (невидимые) грани тела. Из уравнения плоскости для каждрй грани определяются координаты ее направляющего вектора (нормаль к плоскости), а затем определяется угол между направляющим вектором и линией проецирования. Грань невидима, если угол между ними больше 900. можно записать как:
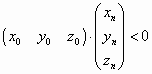
где
![]() -
точка зрения, а
-
точка зрения, а ![]() - нормаль к плоскости.
- нормаль к плоскости.

Рисунок 10.6. Тест видимости
