Алгоритм Кируса-Бека

В работе алгоритма Кируса-Бека используется параметрическое представление отрезка: P_s (t)=P₁+(P₂-P₁)*t;t∈[0;1]. Данный алгоритм позволяет выполнять отсечение не только прямоугольным окном, но и любым выпуклым многоугольником. Рассмотрим отдельное ребро E_i отсекающего многоугольника. Ориентируем нормаль к этому ребру во внешнюю сторону отсекающего многоугольника. Также будем считать, что отсекающий многоугольник обходится против часовой стрелки. Тогда, если ребро – это вектор P_(E(i1)) P_Ei2, то нормаль N_Ei будет пропорциональна (y_Ei2-y_Ei1; x_Ei1-x_Ei2). Обозначим прямую, на которой лежит ребро через L_i. Тогда область, отсекаемая прямой L_i, соответствует точкам P, для которых скалярное произведение векторов (P-P_Ei)) и N_Ei больше 0 (P_Ei — любая точка на ребре E_i). Точка пересечения прямой, на которой лежит отрезок, с отсекающей прямой L_i находится из уравнения ((P_s(t)-P_Ei,N_Ei=0. Решая это уравнение, находим t. Для описываемого алгоритма также важно в каком направлении (внутрь окна или из него) проходит точка при движении по отрезку от P₁ к P₂. Это определяется знаком ((P₂-P₁ ),N_Ei. Будем обозначать такие точки пересечения как: После того, как рассчитаны координаты t для всех возможных пересечений с прямыми L_i, следует выбрать максимальную координату из потенциально входящих и минимальную из потенциально выходящих (t_ВхМакс;t_ВыхМин). Если прямая, на которой лежит отрезок P₁ P₂, пересекает отсекающий многоугольник, то t_ВхМакс<t_ВыхМин. В этом случае, если пересечение [t₁,t₂]=[t_ВхМакс,t_ВыхМин]∩[0,1] непусто, то P_s(t₁) P_s(t₂) и будет искомым отсечённым отрезком, в противном случае отрезок полностью лежит вне отсекаемой области.

Метод Гуро

Этот метод предназначен для создания иллюзии гладкой криволинейной поверхности, описанной в виде многогранников или полигональной сетки с плоскими гранями. Если каждая плоская грань имеет один постоянный цвет, определенный с учетом отражения, то различные цвета соседних граней очень заметны, и поверхность выглядит именно как многогранник. Казалось бы, этот дефект можно замаскировать за счет увеличения количества граней при аппроксимации поверхности. Но зрение человека имеет способность подчеркивать перепады яркости на границах смежных граней - такой эффект называется эффектом полос Маха. Поэтому для создания иллюзии гладкости нужно намного увеличить количество граней, что приводит к существенному замедлению визуализации - чем больше граней, тем меньше скорость рисования объектов.

Метод Гуро основывается на идее закрашива­ния каждой плоской грани не одним цветом, а плавно изменяющимися оттенками, вычисляемыми путем интерполяции цветов примыкающих граней. Закрашивание граней по методу Гуро осуществляется в четыре этапа.

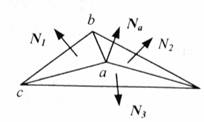
Рис. 1 Нормаль в вершине

	Вычисляются нормали к каждой грани.
	Определяются нормали в вершинах. Нормаль в вершине определяется усреднением нормалей примыкающих граней (рис. 1).
	На основе нормалей в вершинах вычисляются значения интенсивностей в вершинах согласно выбранной модели отражения света.
	Закрашиваются полигоны граней цветом, соответствующим линейной интерполяции значений интенсивности в вершинах.

Вектор нормали в вершине (a) равен

Определение интерполированных значений интенсивности отраженного све­та в каждой точке грани (и, следовательно, цвет каждого пиксела) удобно выполнять во время цикла заполнения полигона. Рассмотрим заполнение контура грани горизонталями в экранных координатах (рис. 2).

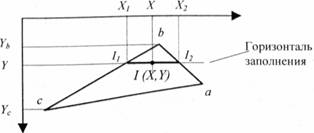
Рис. 2. Заполнение контура грани

Интерполированная интенсивность I в точке (X,Y) определяется исходя из пропорции

 

Отсюда

Значения интенсивностей I₁ и I₂ на концах горизонтального отрезка представляют собой интерполяцию интенсивности в вершинах:

или