Растровая развертка сплошных областей. Закраска ограниченной области

Для закраски ограниченной области используется алгоритм с затравкой. Предполагается, что задана граница области в виде произвольной простой замкнутой линии и указана одна из внутренних точек области. Такая точка называется затравочной. Требуется закрасить нужным цветом связную компоненту области, содержащую затравочный пиксел. Связная компонента области определяет соседние с затравочным пикселом точки (4-х или 8-связные).

Можно представить, что в затравочной точке находится источник, заливающий всю область заданным цветом.

Идея заливки области конструктивно реализуется через использование стека.

Стек - это линейный массив (или список) элементов. В данный список можно вставлять новые элементы и удалять из него элементы. Все вставки и удаления производятся только с одного конца. Это означает, что последний вставленный элемент будет первым извлечен и обработан.

Итак, алгоритм заливки, использующий стек, весьма прост:

1. Положить затравочный пиксел в стек.

2. Если стек не пуст, то извлечь из него пиксел и закрасить. Иначе, если стек пуст, то стоп.

3. Просмотреть все пикселы, соседние с данным.

4. Если соседний пиксел не принадлежит границе и не окрашен в заданный цвет, то поместить его в стек.

5. Перейти к п.2.

Но данный алгоритм весьма неэффективен, т.к. в нем неоднократно просматриваются одни и те же пикселы, а величина стека бесконтрольно растет.

Эффективным является построчный алгоритм заполнения с затравкой.

Будем построчно сканировать экранную плоскость. Отметим, что на каждой строке множество пикселов, подлежащих закраске, состоит из интервалов внутри ограниченной области закраски. Эти внутренние интервалы отделены друг от друга интервалами из пикселов, принадлежащих границе или внешней области.

Отметим также, что пикселы, образующие связный внутренний интервал, соседствуют с пикселами на и под ними, которые являются либо граничными, либо внутренними.

Внутренние пикселы на и под внутренним интервалом в рассматриваемой строке считаются затравочными для соответствующих строк.

Тогда алгоритм выглядит так:

1. Положить затравленный пиксел в стек.

2. Если стек не пуст, то извлечь из него пиксел. Иначе, если стек пуст, то стоп.

3. Закрасить максимально возможный интервал, в котором находится пиксел, влево и вправо до граничных пикселов.

4. Заполнить крайнюю левую и крайнюю правую точки полученного интервала.

5. В соседних строках над и под интервалом найти не закрашенные внутренние пикселы (начать с левой граничной в право).

6. Т.к. они объединены в интервалы, то в каждом из них найти крайние правые пикселы и положить их в стек.

7. Перейти к п.2.

Алгоритм заполняет замкнутую область, в том числе и с отверстиями.

Алгоритмы отсечения отрезков Отсечение отрезков

Самой простой задачей отсечения является задача отсечения отрезков. Сформулируем её на конкретном примере. Будем считать, что область вывода задаётся прямоугольником ABCD. Рассмотрим пример, и в качестве отсекаемой фигуры возьмём треугольник PRQ. 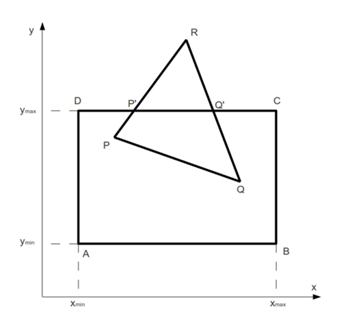Процесс отсечения должен выполняться полностью автоматически. Т.е. для отрисовки треугольника PRQ должны выполниться только команды отрисовки отрезков PQ;PP';Q' Q. При этом координаты точек P';Q' заранее не известны. На практике возможно большое количество взаимных расположений точек отрезка и области вывода. Это разнообразие делает операцию отсечения весьма нетривиальной с алгоритмической точки зрения. Для решения этих задач созданы алгоритмы отсечения.