Задачи компьютерной графики и ее место среди других методов обработки информации 3

Основные направления компьютерной графики. Основные структурные элементы системы машинной графики 5

Виды данных, представленных в форме изображений 6

КЛАСС 1: ТОНОВЫЕ И ЦВЕТНЫЕ ИЗОБРАЖЕНИЯ 6

КЛАСС 2: ДВУХУРОВНЕВЫЕ ИЛИ ПРЕДСТАВЛЯЕМЫЕ В НЕСКОЛЬКИХ «ЦВЕТАХ» ИЗОБРАЖЕНИЯ 6

КЛАСС 3: НЕПРЕРЫВНЫЕ КРИВЫЕ И ЛИНИИ 6

КЛАСС 4: ТОЧКИ ИЛИ МНОГОУГОЛЬНИКИ 6

Виды данных, представленных в форме изображений 8

Понятие изображения 8

Понятие о структуре изображения. Основные графические элементы (примитивы) 9

 Графические элементы (примитивы). 9

Видимые и невидимые поверхности. Ограничения на сложность изображения 10

Ограничения на сложность изображения 11

Тесты пересечения на плоскости 12

Пересечение двух прямых на плоскости 12

Пересечение двух отрезков в плоскости 12

Пересечение плоскости и прямой 13

Тесты принадлежности. Тест видимости 15

Тесты принадлежности. 15

Тест видимости 15

Тесты глубины 17

Алгоритмы удаления невидимых поверхностей 19

Алгоритм сканирующей прямой Уоткинса 20

Алгоритм Робертса 21

Если скалярное произведение уравнения плоскости и этой точки меньше 0, то необходимо поменять знак уравнения этой плоскости, чтобы отразить правильное направление внешней нормали. Остается только вычислить скалярное произведение уравнения плоскости на точку, в которой находится наблюдатель. Если это скалярное произведение меньше 0, то плоскость невидима и необходимо удалить весь многоугольник, лежащий в этой плоскости. Запись этого алгоритма на псеводокоде приводится ниже. 21

Растровое представление геометрических объектов. Растровая развертка отрезка 23

Растровая развертка отрезка. 24

Растровая развертка сплошных областей. Закраска многоугольников 26

Закраска многоугольников. 26

Растровая развертка сплошных областей. Закраска ограниченной области 28

Алгоритмы отсечения отрезков 30

В работе алгоритма Кируса-Бека используется параметрическое представление отрезка: P_s (t)=P₁+(P₂-P₁)*t;t∈[0;1]. Данный алгоритм позволяет выполнять отсечение не только прямоугольным окном, но и любым выпуклым многоугольником. Рассмотрим отдельное ребро E_i отсекающего многоугольника. Ориентируем нормаль к этому ребру во внешнюю сторону отсекающего многоугольника. Также будем считать, что отсекающий многоугольник обходится против часовой стрелки. Тогда, если ребро – это вектор P_(E(i1)) P_Ei2, то нормаль N_Ei будет пропорциональна (y_Ei2-y_Ei1; x_Ei1-x_Ei2). Обозначим прямую, на которой лежит ребро через L_i. Тогда область, отсекаемая прямой L_i, соответствует точкам P, для которых скалярное произведение векторов (P-P_Ei)) и N_Ei больше 0 (P_Ei — любая точка на ребре E_i). Точка пересечения прямой, на которой лежит отрезок, с отсекающей прямой L_i находится из уравнения ((P_s(t)-P_Ei,N_Ei=0. Решая это уравнение, находим t. Для описываемого алгоритма также важно в каком направлении (внутрь окна или из него) проходит точка при движении по отрезку от P₁ к P₂. Это определяется знаком ((P₂-P₁ ),N_Ei. Будем обозначать такие точки пересечения как: После того, как рассчитаны координаты t для всех возможных пересечений с прямыми L_i, следует выбрать максимальную координату из потенциально входящих и минимальную из потенциально выходящих (t_ВхМакс;t_ВыхМин). Если прямая, на которой лежит отрезок P₁ P₂, пересекает отсекающий многоугольник, то t_ВхМакс<t_ВыхМин. В этом случае, если пересечение [t₁,t₂]=[t_ВхМакс,t_ВыхМин]∩[0,1] непусто, то P_s(t₁) P_s(t₂) и будет искомым отсечённым отрезком, в противном случае отрезок полностью лежит вне отсекаемой области. 34

Метод Гуро 35

Метод Фонга 37

Модели расчета освещенности граней трехмерных объектов 39

Методы трассировки лучей. Метод прямой трассировки лучей 41

Классический метод обратной трассировки лучей 42

Методы повышения качества изображения при обратной трассировке лучей 45

Текстурные карты и свойства материалов. Работа с растровыми картами (BMP, PNG, JPEG) 45

Отображение шероховатости (bump-mapping) 45

Сглаживание (antialiasing) 45

Кубические сплайны 46

Задачи компьютерной графики и ее место среди других методов обработки информации

Обработка информации, представленной в виде изображений, на ЭВМ имеет множество разновидностей и массу практических приложений. Эту область обработки информации обычно принято разделять на три направления: машинную графику, обработку изображений и распознавание изображений.

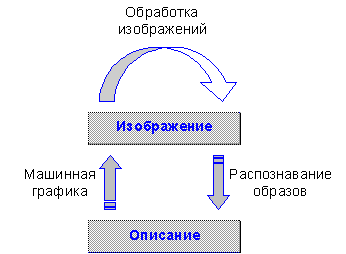
Задача машинной графики — воспроизведение изображений в тех случаях, когда исходной является информация неизобразительной природы; это направление имеет широкий спектр приложений. Термин интерактивная машинная графика относится к устройствам и системам, в которые пользователь вводит исходные данные, сформулированные в терминах порождаемого визуального отображения (например, требуется провести на экране прямую между двумя точками, указанными пользователем).

Выделим некоторые направления компьютерной графики (отметив, что это выделение достаточно условно):

• иллюстративное, которое можно понимать расширительно, начиная с пояснений (визуализации) результатов эксперимента и кончая созданием рекламных роликов;

• саморазвивающее - компьютерная графика должна обслуживать свои потребности, расширяя свои возможности и совершенствуя их;

• исследовательское, в котором инструментарий компьютерной графики начинает играть роль, во многом подобную той, которую в свое время сыграл микроскоп. 

Компьютерная графика и геометрия базируются на таких дисциплинах, как различные разделы геометрии (аналитическая, начертательная, дифференциальная, проективная, прикладная), программирование для ЭВМ, элементы вычислительной математики, понятия о формальных языках, применимых в общении человека и Машины.

Как программно-математические системы, "живущие и работающие" в электронной среде, машинная графика и геометрия складываются из множества программ и их частей (подпрограмм, моделей)  и вызываемых в нужные моменты, в том числе "под управлением" других программ - проектных, конструкторских, ориентированных на решение конкретных задач. Так, системы автоматизированного проектирования состоят из многих частей — подсистем, нацеленных на решение задач разного плана — конструктивных, экономических, технологических и т.д. Машинная графика и геометрия — важные, существенные подсистемы в системах автоматизированного проек­тирования. В конкретных случаях графика и геометрия могут быть объединены в одну программную систему (подсистему).

 Общей основой почти для всех применений машинной геометрии и графики являются двумерные и трехмерные ко­ординатные системы и их преобразования. Подобный геометрический фундамент, общие уравнения, алгоритмы, методы решения задач составляют методическое и математическое "ядро", на которое дальше уже наслаиваются специфические и иногда оригинальные алгоритмы и программы. Таким образом, сама графическая или геометрическая программная система неоднородна, обычно состоит из ряда "слоев" или иерархических уровней.

Сферы применения компьютерной графики:

САПР (системы автоматизированного проектирования);

деловая графика (графическое представление данных);

визуализация процессов и явлений в научных исследованиях (компьютерное графическое

моделирование);

медицина (компьютерная томография, УЗИ и т.д.);

геодезия и картография (ГИС);

полиграфия (схемы, плакаты, иллюстрации);

сфера массовой информации (графика в Интернете, иллюстрации, фото);

кинематография (спецэффекты, компьютерная мультипликация);

быт (компьютерные игры, графические редакторы, фотоальбомы).