4.2. Анализ фундаментальных свойств уоу.

4.2.1. Определение характеристического полинома и спектра системной матрицы, оценка устойчивости.

Xpkoeff=poly(A)

Характеристический полином:

W(p)=p4+18p3+298p2+948p+262

spektr=eig(A)

Корни:

-7.4183 +13.4569i

-7.4183 -13.4569i

-0.3050

-3.6384

Объект является устойчивым, т.к. корни имеют отрицательные вещественные части.

4.2.2. Оценка управляемости, наблюдаемости и полноты уоу.

Матрица управляемости:

Матрица наблюдаемости:

Найдём ранги матриц:

Ранги матриц равны между собой, следовательно, объект является полностью управляемым и наблюдаемым.

4.2.3. Преобразование мв мм уоу к различным базисам.

Основная нормальная (ОН) форма:

Транспонированная основная нормальная (ТОН) форма:

4.3.Синтез динамического наблюдателя состояний.

Синтезируем наблюдатель Калмана для объекта, заданного матрицами в ОН форме::

Выписываем ХП по последней строке А^ОН: p⁴+18.8p³+295.7p²+947.6p+262=0

Корни ХП: p₁=-7+13.4j, p₂=-7-13.4j, p₃=3.64, p₄=0.3.

Выбираем чмсла левее меньшего корня: p₁=-8, p₂=-8.5, p₃=-9, p₄=-9.5.

ХП_набл=(p-p₁) (p-p₂) (p-p₃) (p-p₄)

ХП_набл : p⁴+35p³+458,75p²+2668,75p+5814=0

; ;

Система уравнений для наблюдателя:

;

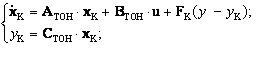
Рисунок 4.3 – Структурная схема объекта с наблюдателем.

Рисунок 4.4 – Переходный процесс по ошибке (y-y_н)

4.4. Реализация модального управления уоу.

Построение системы модального управления для объекта вида:

; ;

N(p): p⁴+35p³+459p²+2669p+5814=0

Корни ХП: p₁=-10+1.6j, p₂=-10-1.6j, p₃=-7+1.1j, p₄=-7-1.1j.

Выбираем чмсла левее меньшего корня: p₁=-10.5, p₂=-11, p₃=-11.5, p₄=-12.

N^c(p)=p⁴+45p³+759p²+5681p+15939=0

Рисунок 4.5 – Структурная схема модального управления объекта.

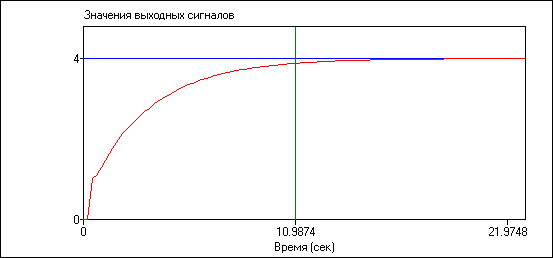
Рисунок 4.6 – Переходный процесс системы.

Рисунок 4.7 – ЛАЧХ и ЛФЧХ системы.

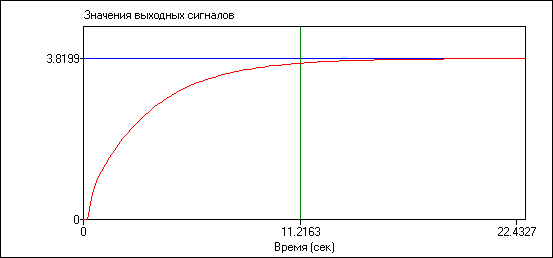
Рисунок 4.8 – Переходный процесс X_1Н.

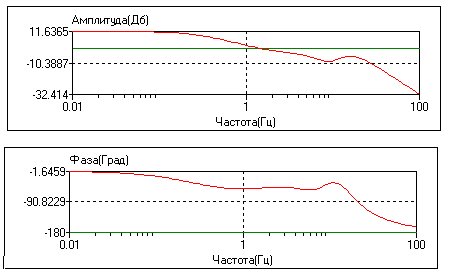
Рисунок 4.8 – ЛАЧХ и ЛЧФХ X_1Н.

Рисунок 4.9 – Переходный процесс X_2Н.

Рисунок 4.9 – ЛАЧХ и ЛЧФХ X_2Н.

Заключение.

В ходе расчётной работы был исследован объект управления по двум входам: получены графики переходных процессов, ЛАЧХ и ЛФЧХ. Была улучшена устойчивость системы с помощью ПД регулятора.

Так же ММ ОУ была преобразована в матрично-векторную форму, по которой можно сказать, что объект является наблюдаемым и управляемым. Был синтезирован динамический наблюдатель состояний и реализовано модальное управление УОУ. По построенным переходным процессам и графикам ЛАЧХ и ЛЧФХ системы и переменных состояний можно сделать вывод, что ошибка стремится к нулю, система является устойчивой.

14