Полюсы(×):

№ Значения

1 -90.0484061442002+0i

2 -14.2857142857143+0i

3 -3.20913026123325+3.22707597784045i

4 -3.20913026123325-3.22707597784045i

5 -2.85714285714286+0i

Рисунок 2.5 – Расположение нулей и полюсов

Коэффициенты числителя: Коэффициенты знаменателя

Т₁ = 1/26.16= 0,038 Т₁ = 1/90.05= 0,011

Т₂ = 1/6.67=0.15 Т₂ = 1/14.28=0.07

Т₃ = 1/3.97=0.25 Т₃ = 1/2.85=0.35

Т₄² = 1/(3.21 ²+3.23 ²) = 0.048

 = 3.21 /(3.21 ²+3.23 ²) ^0,5 = 0.71

Запишем передаточную функцию в канонической последовательно-структурированной форме записи в виде произведения элементарных полиномов.

Оценка свойств объекта:

Объект является устойчивым, т.к. его характеристический полином не имеет нулевых корней.

Коэффициент усиления равен 0.094;

Порядок астатизма равен 0;

Колебательность  = 0.71;

2.2 Получение и исследование динамических и частотный характеристик УОУ.

1. Канал входа u1.

Первый канал входа

Частотные характеристики:

Рисунок 2.6 – ЛАЧХ

Рисунок 2.7 – ЛФЧХ

Рисунок 2.8– ВЧХ

Рисунок 2.9– МЧ

Рисунок 2.10– АФЧХ.

2. Второй канал входа u1.

Частотные характеристики:

Рисунок 2.11 – ЛАЧХ.

Рисунок 2.12 – ЛФЧХ.

Рисунок 2.13 – ВЧХ.

Рисунок 2.14 – МЧХ.

Рисунок 2.15 – АФЧХ.

3. Исследование возможностей и простейших вариантов управления объектом.

Передаточная функция 4-го порядка, астатизм 2-го порядка.

Частотные характеристики и переходный процесс объекта управления:

Рисунок 3.1 – ЛАЧХ и ЛФЧХ .

Рисунок 3.2 – Переходный процесс.

Оценка возможностей статического управления объектом.

3.1 ПД-закон регулирования

Wпд(p)=K_р+Тд(р).

Методика исследования сводится к оценке значений настроек K_р и Тд, обеспечивающих требуемые запасы устойчивости.

Определим расчетное значение величины Тд. Полагая, что начальное значение Кр = 1, то величину Тд определяют из соотношения:

Далее - значение частоты, при котором фазовая характеристика объекта управления (рис. 3.1) опускается ниже ординаты ``-π`` на 10 угловых градусов.

Строим ЛАЧХ и ЛФЧХ с ПД-регулятором. Значение Т=14.3

Вводим полученное значение в передаточную функцию регулятора и определяем запасы устойчивости по ЛАЧХ и ЛФЧХ.

Рисунок 3.3 -ЛАЧХ и ЛФЧХ разомкнутой САУ с ПД-регулятором

Запас устойчивости по амплитуде равен бесконечности, а запас устойчивости по фазе - 2 градуса.

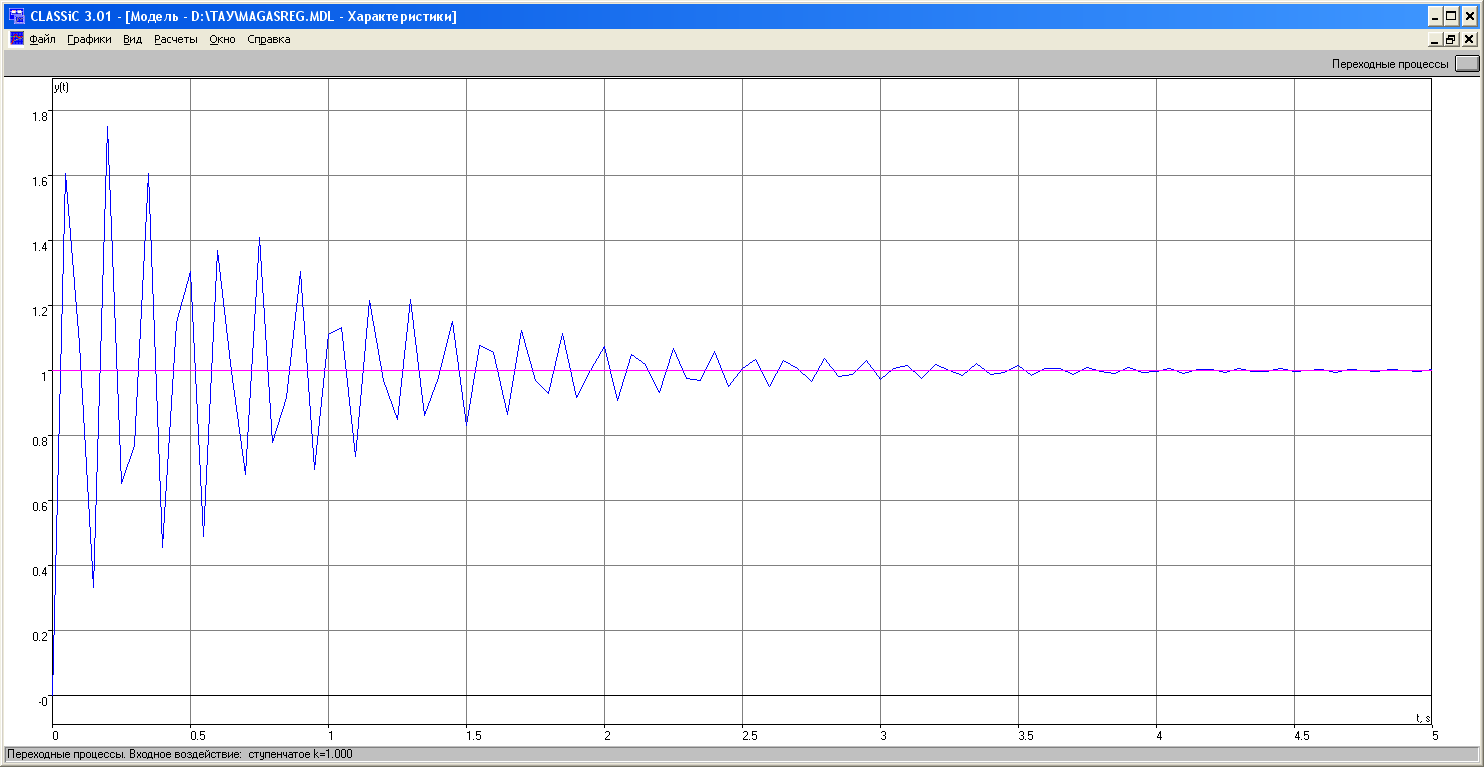
Рисунок 3.4 – Переходной процесс объекта управления с ПД- регулятором

4. Анализ фундаментальных свойств объекта в мв форме описания.

4.1. Преобразование мм оу в матрично-векторную форму описания.

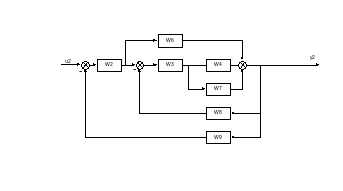
Рисунок 4.1 – Структурная схема объекта управления по второму входу.

; ; ; ; ;

; ; ; .

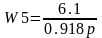Представим каждый элемент схемы через элементарные звенья.

Рисунок 4.2 – Структурная схема объекта, выраженная через элементарные звенья.

Общий вид МВ ММ: