2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ И ИССЛЕДОВАНИЕ 1

УСЛОВНОГО ОБЪЕКТА УПРАВЛЕНИЯ……………………………….5 1

4.2.1. Определение характеристического полинома и спектра 1

системной матрицы, оценка устойчивости………………………………….19 1

2. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ И ИССЛЕДОВАНИЕ УСЛОВНОГО ОБЪЕКТА УПРАВЛЕНИЯ. 4

Нули(+): 5

Полюсы(×): 5

Нули(+): 7

Полюсы(×): 7

4.2. Анализ фундаментальных свойств уоу. 20

4.2.1. Определение характеристического полинома и спектра системной матрицы, оценка устойчивости. 20

4.3.Синтез динамического наблюдателя состояний. 21

Содержание.

Введение……………………………………………………………………2

1. ВЫБОР ВАРИАНТА……………………………………………………3

2. Математическое описание и исследование условного объекта управления……………………………….5

2.1 Получение ПФ по каналам внешних воздействий……………………5

2.2 Получение и исследование динамических и частотный

характеристик УОУ…………………………………………………………9

3. ИССЛЕДОВАНИЕ ВОЗМОЖНОСТЕЙ И ПРОСТЕЙШИХ

ВАРИАНТОВ УПРАВЛЕНИЯ ОБЪЕКТОМ………………………………13

3.1 ПД-закон регулирования…………………………….………………….15

4. АНАЛИЗ ФУНДАМЕНТАЛЬНЫХ СВОЙСТВ ОБЪЕКТА

В МВ ФОРМЕ ОПИСАНИЯ…………………………………………………17

4.1. Преобразование ММ ОУ в матрично-векторную форму описания…..17

4.2. Анализ фундаментальных свойств УОУ……………………………….19

4.2.1. Определение характеристического полинома и спектра системной матрицы, оценка устойчивости………………………………….19

4.2.2. Оценка управляемости, наблюдаемости и полноты УОУ……………19

4.2.3. Преобразование МВ ММ УОУ к различным базисам………………..20

4.3.Синтез динамического наблюдателя состояний…………………………20

4.4. Реализация модального управления УОУ……………………………….22

Заключение……………………………………………………………………..25

1. Выбор варианта.

Исходными материалами КР являются структурная схема условного объекта управления (УОУ) и математические модели структурных звеньев этой схемы. Выбор индивидуального варианта этих данных осуществляется с использованием обобщённой структурной схемы.

Вариант №101.

В соответствии с этим номером по указанным в таблицам выбираются передаточные функции обобщённой структурной схемы и их параметры (коэффициенты).

j=101-72*1=29

; ; ; ;

i=105-4*26=1

Возмущающее воздействие – .

; ;

j=101-14*7=3

; ; ; .

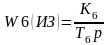j=101-13*7=10

к₀=0,23; к₁=7,8; к₂=0,73; к₃=4,8; к₄=0,18;

к₅=3,2; к₆=0,27; к₇=1,9; к₈=0,54; к₉=6,1.

T_i=T_i^табл* к_0, j=101-17*5=16;

T₂=8,3 *0,23=1,91; T₃=0,16 *0,23=0,04; T₄=1,5 *0,23=0,35;

T₆=3,7*0,23=0,85; T₇=0,32*0,23=0,07; T₉=0,65*0,23=0,15.

; ; ; ; ;

; ; ; .

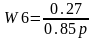Рисунок 1 - Общая схема

2. Математическое описание и исследование условного объекта управления.

2.1 Получение пф по каналам внешних воздействий.

Рисунок 2.1 - Структурная схема объекта управления

Рисунок 2.2 - Структурная схема объекта управления по первому каналу входа u1.

Эквивалентная передаточная функция по каналу входа u1:

Преобразуем эту передаточную функцию в каноническую форму записи:

Полученная передаточная функция имеет 5-й порядок и обладает астатизмом 1-го порядка.

Найдем корни числителя и знаменателя передаточной функции.

Нули(+):

№ Значения

1 -26.7315639188169+0i

2 -7.21704342462131+0i

3 -3.35774237955113+0i

4 -0.637674153244011+0i

Полюсы(×):

№ Значения

1 -90.0484061442002+0i

2 -14.2857142857143+0i

3 -3.20913026123324+3.22707597784046i

4 -3.20913026123324-3.22707597784046i

5 -2.85714285714285+0i

6 0+0i

Рисунок 2.3 – Расположение нулей и полюсов

Коэффициенты числителя: Коэффициенты знаменателя

Т₁ = 1/26.73 = 0,037 Т₁ = 1/90.05= 0,011

Т₂ = 1/7.22=0.13 Т₂ = 1/14.28=0.07

Т₃ = 1/3.36=0.29 Т₃ = 1/2.86 = 0.35

Т₄ = 1/0.64=1.56 Т₄² = 1/(3.21 ²+3.23 ²) = 0.048

 = 3.21 /(3.21 ²+3.23 ²) ^0,5 = 0.71

Запишем передаточную функцию в канонической последовательно-структурированной форме записи в виде произведения элементарных полиномов.

Оценка свойств объекта:

Объект является неустойчивым, т.к. его характеристический полином имеет нулевой корень.

Коэффициент усиления равен 0.446;

Порядок астатизма равен 1;

Колебательность  = 0.71;

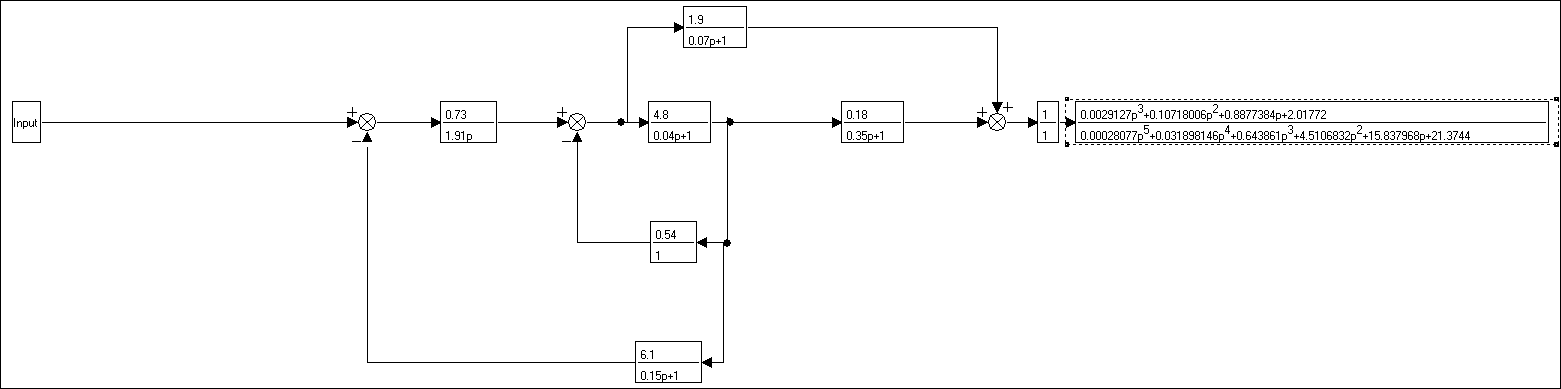
Рисунок 2.4 – Структурная схема объекта управления по первому каналу входа u1.

Эквивалентная передаточная функция по каналу входа u1:

Преобразуем эту передаточную функцию в каноническую форму записи:

Полученная передаточная функция имеет 5-й порядок и не обладает астатизмом.

Найдем корни числителя и знаменателя передаточной функции.

Нули(+):

№ Значения

1 -26.1585154674398+0i

2 -6.66666666666667+0i

3 -3.97231160022936+0i