Завдання 2. Множинна регресія та фіктивні регресори при сезонному прогнозуванні

Фірма “А” на період 1-4 квартал 2004 р. бажає отримати прогноз обсягу продажу товарів. Даними про обсяги їх продажу за попередні 5 років скористатися з 1-го завдання лабораторної роботи №3.

1. Визначити значення фіктивних регресорів для моделі множинної регресії.

2. Побудувати модель множинної регресії від фіктивних регресорів.

3. Знайти відповідні сезонні компоненти для кожного кварталу та 95%-ві довірчі інтервали для коефіцієнтів регресії.

4. Знайти прогноз на наступні 4 квартали. Значення отриманого прогнозу та сезонних компонент порівняти із значеннями, отриманими в лабораторній роботі №3.

5. По результатам прогнозування зробити висновки.

Методичні вказівки до виконання завдання 2

1. Спочатку запишемо фактичні дані у вигляді таблиці:

   Порядковий № кварталу

   Обсяг продажу

2. Побудуємо лінійне рівняння регресії Y по i, в якому Y – це обсяги продажу, і – порядковий № кварталу.

3. Підставимо значення і в рівняння регресії та знайдемо відповідні значення .

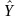4. Розрахуємо детрендове значення для кожного кварталу за формулою:

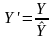
Значення занесемо в таблицю, яка має структуру:

Порядковий № кварталу, і

Обсяг продажу, Y

Значення тренда,

Детрендове значення, Y’

5. Розглянемо модель множинної регресії:

де ;

Ф⁽¹⁾ = 1 для 1-го кварталу і Ф⁽¹⁾ = 0 – для всих інших кварталів;

Ф⁽²⁾ = 1 для 2-го кварталу і Ф⁽²⁾ = 0 – для всих інших кварталів;

Ф⁽³⁾ = 1 для 3-го кварталу і Ф⁽³⁾ = 0 – для всих інших кварталів.

Для знаходження коефіцієнтів регресії побудуємо таблицю із значеннями фіктивних регресорів, структура якої буде мати вигляд:

Порядковий № кварталу, і

Ф(1)

Ф(2)

Ф(3)

6. Для знаходження коефіцієнтів множинної регресії застосуємо метод найменших квадратів. В якості матриці Х виступають значення регресорів, в якості матриці Y – значення .

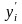7. Для отриманих коефіцієнтів регресії визначаємо 95%-ві довірчі інтервали за формулою:

де - значення t-критерію Ст’юдента при n-спостереженнях та k-коефіцієнтів регресії;

s – стандартна помилка регресії;

z_jj – j-ий діагональний елемент матриці (M^TM)^-1.

8. Використовуючи отримані значення параметрів регресії, визначаємо сезонні компоненти наступним чином:

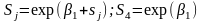
9. Знаходимо 95% довірчий інтервал для S₄ , як і для параметрів регресії. Якщо на даному інтервалі коефіцієнт не приймає нульового значення, то статистично значимий і його можна використовувати для подальших розрахунків.

10. Щоб отримати 95%-вий довірчий інтервал для S₁, потрібно розглянути наступну модель множинної регресії:

Проводимо аналогічні розрахунки, як і для знаходження S₄ (див.п. 6-9).

11. Щоб отримати 95%-вий довірчий інтервал для S₂, потрібно розглянути наступну модель множинної регресії:

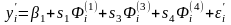
Проводимо аналогічні розрахунки, як і для знаходження S₄ та S₁ (див.п. 6-9).

12. Щоб отримати 95%-вий довірчий інтервал для S₃, потрібно розглянути наступну модель множинної регресії:

Проводимо аналогічні розрахунки, як і для знаходження S₄, S_1, S₂ (див.п. 6-9).

13. Після знаходження довірчих інтервалів і перевірки коефіцієнтів сезонності на значимість, знаходимо прогноз на 4 наступні квартали шляхом перемноження відповідного значення коефіцієнту сезонності на останні значення Y (наприклад, S₁ помножити на останнє значення Y, що відповідає першому кварталу).