Методичні вказівки до виконання завдання 6

Лінійна модель заданих динамічних рядів описується формулою

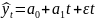, (2.35)

де 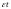- випадкова величина.

Прогнозна модель для заданого типу рівняння матиме вигляд:

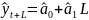(2.36)

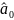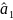_{Для розрахунку параметрів} і використовують систему рівнянь Брауна і знаходять їх через експоненціальні середні і

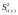
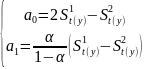, (2.37)

де, - параметр згладжування, який розраховується, як ;

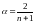n - кількість членів ряду;

і - експоненціальні середні відповідно першого та другого порядків, які розраховуються, як:

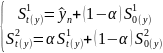(2.38)

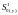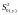, - початкові рівні експоненціальних середніх відповідно першого та другого порядків;

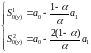, (2.39)

де а_0, а₁ – параметри лінійного рівняння, розраховані методом найменших квадратів;

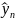- теоретичне значення останнього рівня ряду.

Порядок виконання завдання

1. Методом найменших квадратів знаходять параметри лінійного рівняння /а_0, а₁/, розраховують теоретичні рівні динамічного ряду /див. методик у завданні 3/.

2. Обчислюють параметр згладжування а.

3. Знаходять початкові рівні експоненціальних середніх першого та другого порядків , .

4. Знаходять експоненціальні середні першого та другого порядку і .

5 Розраховують параметри рівняння для прогнозу динаміки і .

6. Визначають прогнозні рівні ряду на п’ять років.

7. Знаходять похибки при лінійному прогнозуванні, використовуючи формулу

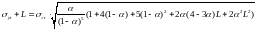(2.40)

де ,

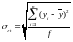де, - середнє арифметичне значення динамічного ряду;

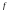- число ступенів вільності ( =n-2).

Завдання 7

На основі динаміки окремих показників, наведених у табл. 2.8. розрахувати тісноту зв'язку між ними, використавши метод парної кореляції.

Вихідні дані

Таблиця 2.8 – Динаміка показників

Рік	Загальний обсяг товарообігу, млрд. грн.	Середньорічний дохід на душу населення, грн.	Чисельність населення, млн. чол.
1	45.5	1716	50.6
2	47.1	1752	50.8
3	48.2	1920	50.8
4	49.4	2112	50.9
5	53.8	2220	51.0
6	60.1	2268	51.2
7	63.3	2364	51.3
8	68.8	2500	51.6
9	73.2	2575	51.7
10	78.3	2904	51.8

Методичні вказівки до виконання завдання 7

Для визначення тісноти зв'язку між двома показниками /факторами/ використовують формулу коефіцієнта парної кореляції

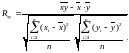(2.41)

де 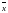та - середнє значення відповідно першого і другого показника;

n - кількість спостережень.

Якщо 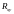=0 - то величини x i y – незалежні;

Якщо | |<0.5 – зв’язок між ними слабкий;

Якщо 0.5<| |<0.8 зв’язок між ними сильний;

Якщо | |=1 зв'язок є функціональним і залежність набуває вигляду лінійної функції

Для оцінки достовірності коефіцієнта кореляції розраховують критерій достовірності.

,

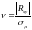де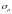 - похибка коефіцієнта кореляції.