Задача № 6 Расчет и назначение посадки с зазором для подшипника скольжения

Исходные данные: 1) номинальный размер подшипника d ; 2) ширина вкладыша или втулки подшипника L ; 3) высотные параметры шероховатости поверхностей вала R_ad и вкладыша или втулки R_aD 4) радиальная нагрузка на цапфу R ; 5) частота вра­щения вала п ; 6) динамическая вязкость масла μ .

Определить: 1) наименьший и наибольший допустимые зазоры; 2) по­садку с зазором.

Иллюстрации: 1) схема подшипника скольжения в состоянии покоя и в рабочем установившемся режиме; 2) схема расположения полей допусков на размеры сопрягаемых поверхностей.

Расчет и назначение посадки с зазором для подшипника скольжения выполняется в следующей последовательности:

1. Определяется среднее удельное давление в подшипнике

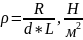
где R - радиальная нагрузка на цапфу, Н;

d - номинальный диаметр подшипника, м;

L - ширина вкладыша или втулки подшипника, м.

2. Задаваясь высотами неровностей трущихся поверхностей отверстия R_aD и вала R_ad, определяется допускаемая толщина поверхностного слоя,

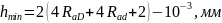
где 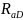— высотный параметр шероховатости отверстия, мкм;

— высотный параметр шероховатости вала, мкм.

3. По частоте вращения вала определяется угловая скорость

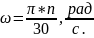
4. Рассчитывается значение коэффициента A_h

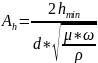
где μ - вязкость масла динамическая, Па*c.

5. По найденному значению A_h определяется по рисунку 2.8 минимальный относительный эксцентриситет Х_min и вычисляется наименьший допустимый

зазор S_min.

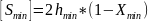
Если величина X_min оказывается меньше 0,3, то по рисунку 2.8 для данного соединения L/d определяют величину А_х, при х = 0,3. После этого рассчитыва­ют наименьший допустимый зазор.

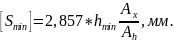
6. По найденному значению A_h определяется по рисунку максимальный от­носительный эксцентриситет Х_max и рассчитывается наибольший допустимый зазор.

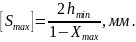
Используя значения 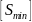и 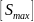по [4] подбирается посадка, при которой выполняется условие

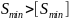
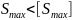
Если этому условию удовлетворяет несколько посадок, то рекомендуется использовать предпочтительные менее точного квалитета. При отсутствии не­обходимой посадки можно ее построить, используя разрешенные поля допус­ков отверстия и вала, или изменить параметры подшипника скольжения и по­вторить расчет.

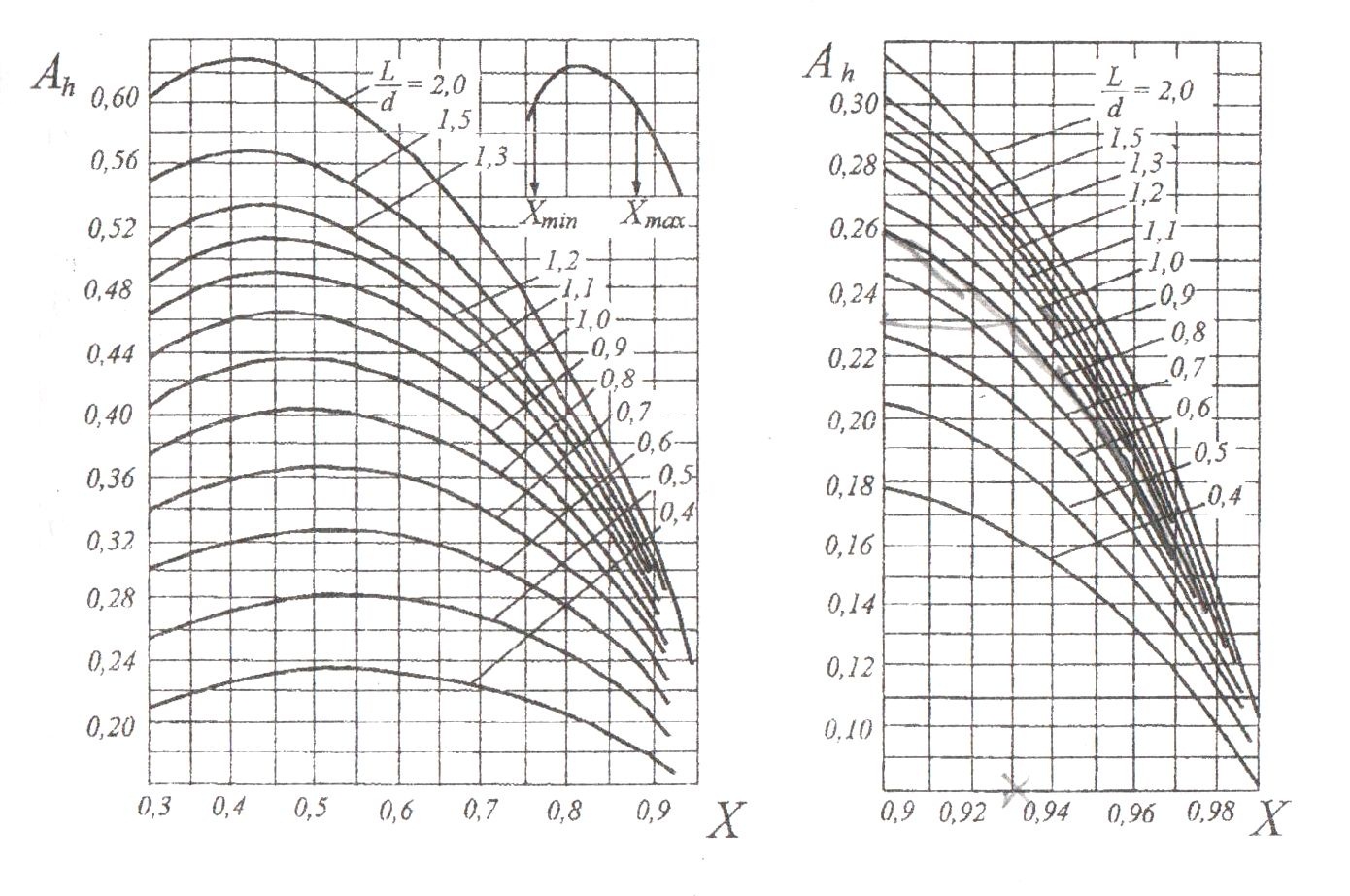
Рисунок 7 – Зависимость коэффициента A_h от относительного эксцентриситета X

Решение:

Данные: D=46 мм ; L=53 мм ; R=4800 Н ; μ=0,04 Па*с. ; n=1000 об/мин ; R_aD=0.1 мкм ; R_ad=0.3 мкм ;

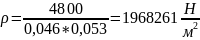
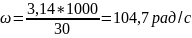
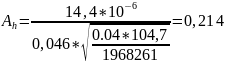
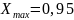
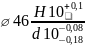
Рисунок 8 - Схема расположения полей и допусков для отверстия и для вала.

Задача №7 Расчет переходной посадки

Исходные данные:

1. Номинальный диаметр соединения: d=215 мм.

2. Допуски вала и отверстия:

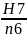
Определить:

1. Максимальный, минимальный и средний натяги.

2. Допуски вала и отверстия.

3. Вероятность зазора и вероятность натяга.

Решение:

1. По номинальному размеру и типу посадки определим максимальный D_max и минимальный D_min размеры отверстия, максимальный d_max и минимальный d_min размеры вала:

Схема расположения полей допусков на размеры сопрягаемых поверхностей изображен на рисунке

Рисунок 9 - Расчетная схема расположения полей допусков отверстия и вала в системе вала.

Размеры вала:

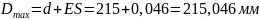
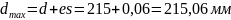
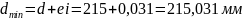
2. По предельным размерам отверстия и вала определяем средний натяг:

Допуски отверстия T_D и вала T_d:

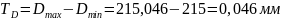
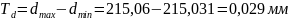
3. Определяем среднее квадратичное отклонение натяга σ_N:

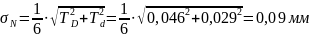
4. Вычисляем предел интегрирования:

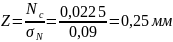
По найденному значению Z определяется функция Ф(Z) (приложение Б)

Z=0,25 тогда Ф(Z) = 0,0987

5. Определяем вероятность натягов P_N и вероятность зазоров P_S в зависимости от предела интегрирования Z:

Если Z < 0 , то