- •Введение
- •Задача № 1 Назначение посадки и обоснование посадки с зазором или переходной
- •Решение.
- •Задача № 2 Расчет рабочего калибра для элемента соединения
- •Задача №3 Назначение посадки в соединении с подшипником качения и требований к точности сопряженных поверхностей деталей
- •Задача №4 Расчет размерной цепи методом полной взаимозаменяемости
- •Задача №5 Расчет размерной цепи теоретическо-вероятностным методом (прямая задача)
- •Задача № 6 Расчет и назначение посадки с зазором для подшипника скольжения
- •Задача №7 Расчет переходной посадки
- •Задача №8 Расчет и назначение посадки с натягом
- •Задача № 9 Разработка рабочего чертежа детали
- •Заключение
- •Библиографический список
Задача №4 Расчет размерной цепи методом полной взаимозаменяемости
Исходные данные:
y6 –вид замыкающего звена по заданному механизму;
Размеры (звенья размерной цепи).
Определить:
Номинальный размер и предельные значения замыкающего звена;
Допуск на замыкающее звено;
Иллюстрации:
Схема размерной цепи;
Таблица с результатами вычислений.
Решение:
Расчет размерной цепи методом полной взаимозаменяемости выполняем в следующей последовательности:
1. Построим схему размерной цепи:

Рисунок 6 – Схема размерной цепи.
2. Составим уравнение размерной цепи:
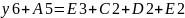
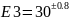
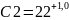
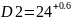
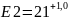
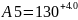
3. Определяем номинальное значение замыкающего звена:
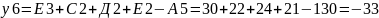 Предельные
значения замыкающего звена определяем
по зависимостям:
Предельные
значения замыкающего звена определяем
по зависимостям:
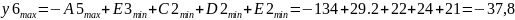
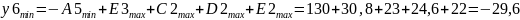
5. Допуск замыкающего звена определяем из соотношения:
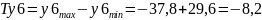
6. Проверка результата на основании закона суммирования погрешностей в линейной размерной цепи:
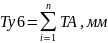
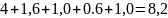
Таблица 3 – Результаты расчета размерной цепи по методу максимума – минимума.
Виды размеров |
Условное обозначение |
Значения размеров, мм |
Предельные отклонения, мм |
Допуски, мм |
Составляющие |
A5 |
|
+4.0 |
4 |
Е3 |
|
|
1.6 |
|
C2 |
|
+1.0 |
1.0 |
|
D2 |
|
+0.6 |
0.6 |
|
Е2 |
|
+0,6 |
1,0 |
|
Замыкающий |
Y6 |
|
|
8,2 |
Задача №5 Расчет размерной цепи теоретическо-вероятностным методом (прямая задача)
Исходные данные: 1)номинальные размеры звеньев (из задачи №4); 2)допуск на замыкающее звено (из задачи №4); 3)закон рассеяния размеров – нормальный (Гаусса); 4)допустимый процент брака (процент риска) P=0.27%.
Определить: 1)допуски на составляющие звенья.
Иллюстрации: 1)таблица с результатами вычислений.
Расчет размерной цепи вероятностным методом выполняется
в следующем порядке:
1. Принимаем, что рассеяние размеров звеньев близко к нормальному закону, т.е. коэффициент относительного рассеяния составляющих звеньев λi ≈1/3, коэффициент относительного рассеяния замыкающего звена λ∑=1/3,
коэффициент αi = 0.
2. Рассчитаем допуски составляющих размеров по способу одной степени точности, принимая процент риска Р = 0,27 %. При Р = 0,27 % коэффициент
процента риска t = 3.
Определяем среднее число единиц допуска составляющих звеньев
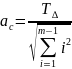
Где T∆ - допуск замыкающего звена, мкм (из задачи № 5);
(т-1) - количество составляющих звеньев в цепи;
i - единица допуска составляющего звена.
Единицы допуска можно определить по зависимости
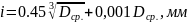
Где Dcp - среднее геометрическое граничных значений интервала, в котором
находится конкретный размер, мм.
По числу ас определяем средний квалитет точности для всех составляющих размеров.
3. Проверяем правильность назначения допусков составляющих звеньев по уравнению
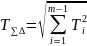 ,мм
,мм
4. Оценим процент риска Р, так как Т∆ ≠ [Т∆ ] по зависимости
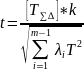
По таблице 2.5 находим значение Р. Если Р ≤ 0,27 %, условие удовлетворяется. Если значение Р > 0,27 %, необходимо выбрать более высокий квалитет точности, проверить правильность назначения допусков составляющих звеньев Т∆ и оценить процент риска Р.
Таблица 4 - Значение коэффициента t при нормальном распределении размеров замыкающего звена для различных процентов риска Р
р, % |
0,01 |
0,05 |
0,1 |
0,27 |
0,5 |
1 |
2 |
3 |
5 |
10 |
32 |
t |
3,89 |
3,48 |
3,29 |
3,00 |
2,81 |
2,57 |
2,32 |
2,17 |
1,96 |
1,65 |
1,00 |
Решение:
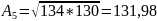
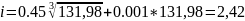
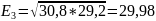
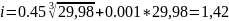
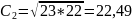
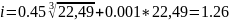
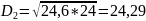
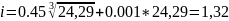
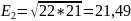
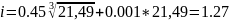
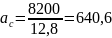
Выбираем 15 квалитет. Назначаем допуски составляющих звеньев
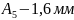
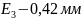
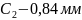
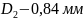
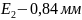
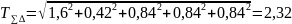
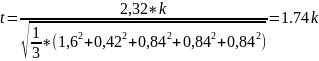
Выбираем k = 2.Тогда t = 3.48. Процент риска по таблице: P ≈ 0.05 %

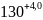
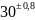
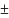 0.8
0.8