2.1.2. Вращающий момент.
На рис. 5 приведена схема Д.М. с подвижной рамкой:
Рис. 5. Схема ДМ с подвижной рамкой.
Сила, действующая на проводнике с током, помещенная в поле постоянного магнита, равна:
где B – индукция (г.с.)
l – активная длина проводника, находящегося в основном потоке постоянного магнита.
Сила, действующая на рамку, имеющую витков:
Для нашей схемы эта сила приложена только к внутренней стороне рамки, т.к. внешняя сторона рамки экранирована от магнитного поля кольцевым ярмом.
Следовательно:
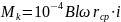
Индукция в зазоре внутрирамочного магнита распределяется по закону, близкому к косинусоидальному:
Следовательно,
2.2 Электродинамические д.М.
Схема ДМ приведена на рис.6.
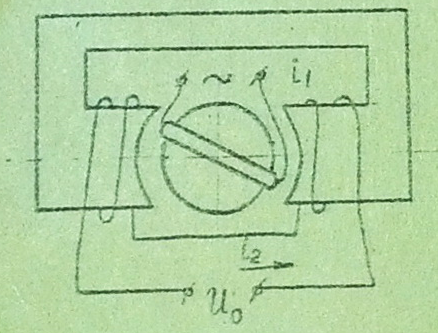
Рис. 6. Схема ДМ.
Величина момента равна:
где
- число намоток рамки.
Значение индукции в воздушном зазоре:
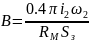
где:
- число витков в неподвижной обмотке,
RM – полное магнитное сопротивление,
-
площадь поперечного сечения потока в
рабочем воздушном зазоре,
-
ток в неподвижной обмотке.
Следовательно:
где
-
крутизна характеристики.
Если магнитное поле в зазоре однородно, корректирующий момент представляет собой функцию тока в рамке и не зависит от угла поворота рамки.
Пусть
тогда
Следовательно, имеется переменная составляющая, оказывающая полезное усредняющее действие на подшипники.
Среднее значение корректирующего момента:
Если
токи
и
сдвинуты по фазу на угол φ, среднее
значение момента зависит от этого сдвига
фазы.
В самом деле
Следовательно:
Среднее значение момента равно:
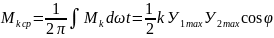
Очевидно, максимальное значение корректирующего момента имеет место при φ=0.