3.4. Интервальная оценка

Интервальная оценка – оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью находится истинное значение оцениваемого параметра. Интервал в интервальной оценке называется доверительным интервалом, задаваемая исследователем вероятность называется доверительной. В практике статистических вычислений применяются стандартные значения доверительной вероятности: 0,95, 0,98 и 0,99 (95%, 98% и 99% соответственно).

Интервальная оценка математического ожидания определяется следующим образом, если исходная выборка распределена по нормальному закону, то можно показать, что оценка математического ожидания в виде среднего имеет дисперсию:

Если при проведении измерительного эксперимента возможно малое число наблюдений или закон распределения неизвестен, то оценка математического ожидания и СКО математического ожидания принимаются равными вычисленным оценкам. При заданной доверительной вероятности можно установить величину доверительного интервала для .

3.5. Построение статистического распределения выборки

Для построения эмпирического статистического распределения необходимо задать последовательность интервалов и соответствующих частот.

Количество интервалов определяется по формуле Стреджесса: 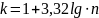, где n – объем выборки;

Длинна интервала находится по формуле:

Центр распределения определяется по формуле:

Границы элементарных интервалов определяются по схеме:

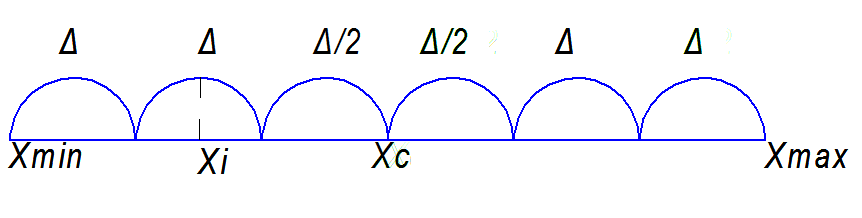
Рис. 16 Границы элементарных интервалов

3.6. Проверка выдвинутой гипотезы о законе распределения исходных данных с доверительной вероятностью 0,95 по критерию Пирсона

Используем для проверки критерий согласия Пирсона (критерий ).

Для того чтобы проверить нулевую гипотезу , необходимо вычислить теоретические частоты и наблюдаемое значение , которое является мерой расхождения данных от теоретического закона:

– теоретическая частота (вероятность) попадания в i-тый интервал.

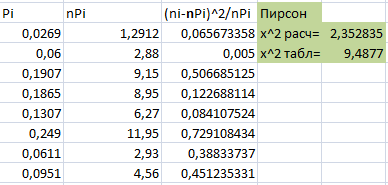
Рис. 17 Расчет критерия Пирсона (при помощи программы Excel)

Найденное значение 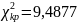сравниваем с расчетным значением 

1. Если нет оснований отвергать гипотезу о распределении выборки по нормальному закону;

2. Если  , гипотеза отвергается.

При этом существует вероятность ошибочного принятия нулевой гипотезы, или ошибочного ее отвержения.

№ – номер интервала;

– нижняя граница интервала;

– верхняя граница интервала;

– середина i-го интервала;

– число значений попавших в i-ый интервала;

– теоретическая вероятность попадания в i-тый интервал;

– нормирующие случайные величины относительно найденного среднего;

– функция Лапласа от нормирующего значения y_i;

=12,087.

=0,639

Исходя из того, что:

Гипотеза о том, что представленный закон распределения является нормальным, принимается.

Идентификация законов распределения представлена на рисунке 18:

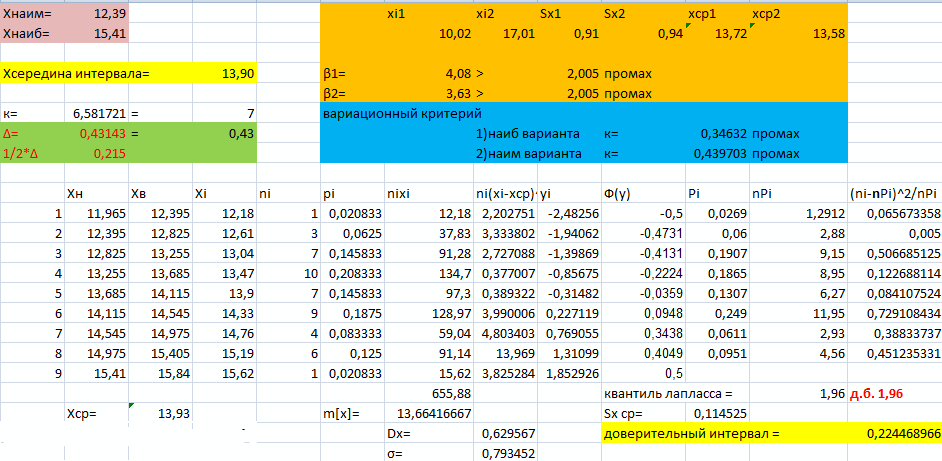
Рис. 18 Идентификация законов распределения

Гистограмма – инструмент, который позволяет наглядно изобразить и легко выявить структуру и характер изменения полученных данных (оценить распределение), которые трудно заметить при их табличном представлении.

Важное преимущество гистограммы заключается в том, что она позволяет наглядно представить тенденции изменения измеряемых параметров качества объекта и зрительно оценить закон их распределения. Кроме того, гистограмма дает возможность быстро определить центр, разброс и форму распределения случайной величины. Строится гистограмма, как правило, для интервального изменения значений измеряемого параметра.

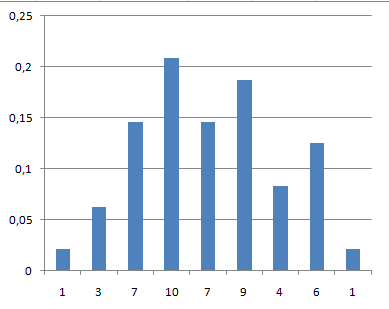
Рис. 19 Гистограмма распределения вероятностей