4. Точность измерения

Точность измерения - характеристика измерения, отражающая степень близости его результатов к истинному значению измеряемой величины. Чем меньше результат измерения отклоняется от истинного значения величины, то есть чем меньше его погрешность, тем выше точность измерения., независимо от того, является ли погрешность систематической, случайной или содержит ту и другую составляющие. Иногда в качестве количественной оценки точности измерения указывают погрешность, однако погрешность является понятием, противоположным точности, и логичнее в качестве оценки точности измерения указывать обратную величину относительной погрешности (без учёта её знака); например, если относительная погрешность равна ±10^—5, то точность равна 10⁵.

5. Источники погрешности

Погрешность обуславливается следующими причинами:

1. математическое описание задачи является не точным, в частности не точно заданы исходные данные описания;

2. применяемый для решения метод часто не является точным: получение точного решения возникающей математической задачи требует неограниченного или неприемлемо большого числа арифметических операций; поэтому вместо точного решения задачи приходится прибегать к приближенному;

3. при вводе данных в машину, при выполнении арифметических операций и при выводе данных производятся округления.

Погрешности, соответствующие этим причинам, называют:

1) неустранимой погрешностью;

2) погрешностью метода;

3) вычислительной погрешностью.

6. Оценка достоверности процедуры контроля

При выполнении контроля решения принимаются в условиях помех, поэтому существует вероятность совершения ошибок первого рода PI (годная деталь признается браком) и ошибок второго рода PII (бракованная деталь признается годной) очевидно что вероятность правильного решения о процедуре контроля вероятность правильного решения:

Оценка вероятности ошибок определяется в области безразмерных величин.

Введем обозначения:

безразмерная величина, характеризующая истинные значения погрешности контролируемого параметра (отклонение от номинального значения):

;

следовательно попадание параметра в допуск можно записать:

.

- безразмерная величина, пропорциональная текущей ошибки измерения , которая находится в пределах :

.

При выполнении измерений на результате сказывается:

1. величина отклонения параметра от номинала;

2. ошибка средства измерения.

Таким образом существует видимое значение контролируемого параметра, которое можно охарактеризовать безразмерной величиной . Величины и являются случайными взаимно независимыми, их можно охарактеризовать функциями распределения (интеграл от плотности)

– плотность распределения случайной величины ;

- плотность распределения случайной величины .

Совместная функция распределения двух случайных величин:

, где

- совместная плотность распределения двух случайных величин.

Совместная плотность распределения:

, тогда

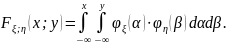
Ошибка I-го рода

Ошибка первого рода или «ложная тревога» — когда нулевая гипотеза отвергается, хотя на самом деле она верна. Вероятность ошибки первого рода: .

Имеют место при условии что контролируемый параметр находится в поле допуска, т.е. при этом видимое значение результата фиксирует выход параметра за пределы допустимых значений:

;

, граничные условия .

Представим область решений для этих условий (область интегрирования для совместной функции распределения)

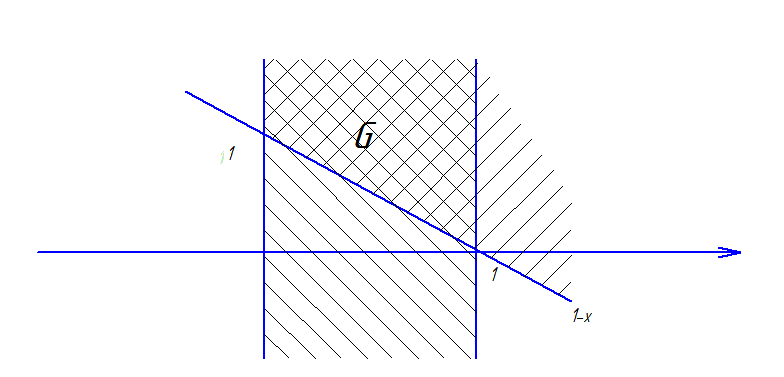
Рис. 5 Область интегрирования для совместной функции распределения

Тогда оценку вероятности ошибок I-го рода можно записать:

Предположим что случайные величины характеризующие погрешности распределены равномерно в пределах:

1. отклонение контролируемого параметра от 12 мк до 65 мк

2. погрешность мк, тогда пределы измерения соответствующих безразмерных величин:

-

-

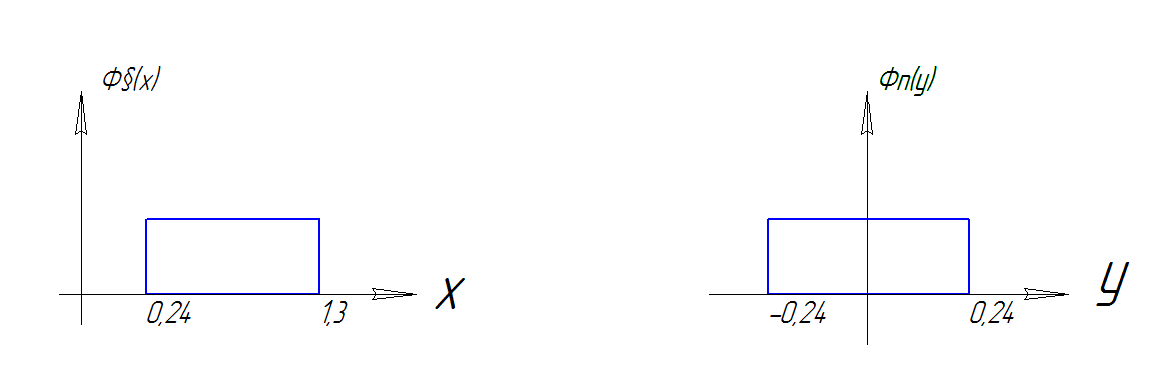
Рис. 6 Пределы измерения безразмерных величин

PI =

Ошибка II-го рода

Ошибка второго рода или «пропуск цели» — когда нулевая гипотеза принимается, хотя на самом деле она не верна. Вероятность ошибки второго рода:

Имеют место при условии, что контролируемый параметр вышел за поле допуска , а видимое значение фиксирует норму

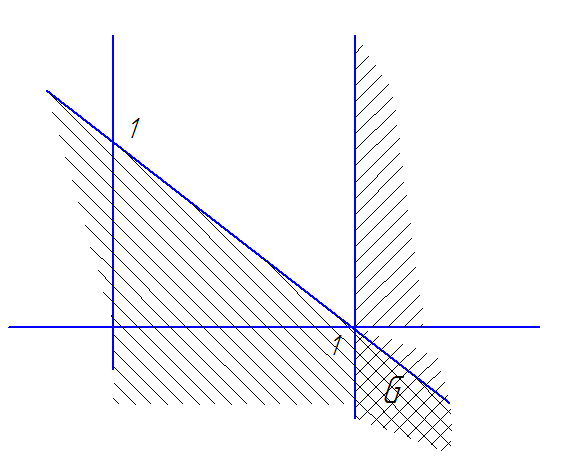
Рис. 7 Область интегрирования для совместной функции распределения

Тогда оценку вероятности ошибок II-го рода можно записать:

PII =

Таким образом при контроле данного изделия с учетом PI и PII вероятность достоверности контроля не менее:

Учитывая что вследствие принятия гипотезы о равномерности распределения погрешностей изготовления контроля и погрешности средства измерения оценки вероятностных ошибок были несколько завышены, оценка достоверности контроля оказывается несколько заниженной.