§ 6.8. Показатели качества сау и методы их определения по распределению корней характеристического уравнения. Интегральные и частотные методы оценки.

1.Показатели качества САУ.

Как было показано выше, устойчивость является необходимым условием практического применения любой реальной системы автоматического управления и регулирования. Вместе с тем, на качество самого процесса регулирования налагаются определенные ограничения, которые выражаются показателями качества САР.

Есть показатели качества, которые характерны для любого изделия, машины, судна и т.п. К ним можно отнести экономичность, простоту изготовления или технологичность, простоту в обслуживании, массогабаритные показатели и т.д.

Ниже будут рассмотрены специфические показатели качества САР, которые характеризуют их динамические свойства в переходном процессе. В соответствии с рис. 1.12 и рис. 1.13, где показаны два вида переходных процессов, к показателям качества будем относить:

- время переходного процесса или время регулирования (оно характеризует быстродействие системы);

- максимальное отклонение в переходный период или величину динамической ошибки ;

- колебательность переходного процесса и величину статической ошибки ; величина статической ошибки определяет точность системы автоматического регулирования.

Из сказанного ясно, что для суждения о перечисленных показателях качества, необходимо построить кривую переходного процесса. Это можно сделать с помощью решения исходного дифференциального уравнения САР, так называемым прямым методом. Он имеет целый ряд трудностей, особенно при решении уравнений высоких порядков. Поэтому в теории управления разработан ряд косвенных методов, позволяющих оценивать основные показатели качества без решения исходных дифференциальных уравнений.

Косвенные методы можно разделить на несколько групп, а именно: анализ качества по распределению корней характеристического уравнения; интегральные оценки; частотные методы.

2. Анализ качества по распределению корней характеристического уравнения впервые был сделан И.А. Вышнеградским (см. п.2.2.1).

Для каждой области диаграммы Вышнеградского (см. рис. 2.5) оказалась оригинальной форма переходного процесса при единичном входном воздействии, как это показано на рис. 2.15 а, б, в.

Рис. 2.15. Формы сходящегося переходного процесса: а) – колебательный; б) - монотонный; в) – апериодический.

3. Интегральные оценки показателей качества.

Они являются комбинированными критериями - оценивают запас устойчивости, быстродействие и статическую ошибку. Интегральные оценки основаны на разработанных условных интегральных показателях, характеризующих достаточно просто отклонение переходного процесса реальной САР от идеального. Под идеальным обычно понимают или ступенчатый процесс, протекающий мгновенно без перерегулирования, или процесс, протекающий по экспоненте с заданными параметрами. Простейшей интегральной оценкой может служить показатель , где - ошибка системы. Показатель представляет собой алгебраическую сумму площадей под кривой переходного процесса (рис. 2.16).

Рис. 2.16. Простейшая интегральная оценка качества САР.

Чем меньше , тем быстрее затухает переходный процесс и тем меньше величина отклонения, т.е. тем выше качество САР. Однако, это справедливо только для систем с апериодическими переходными процессами без перерегулирования, когда не меняется знак ошибки . Качество систем с колебательными переходными процессами характеризуется квадратичной интегральной оценкой , предложенной А.А. Красовским.

Недостатком интегральных оценок является отсутствие наглядного соответствия между значениями показателей I и характеристиками переходных процессов. Трудность применения интегральных оценок для определения показателей качества состоит также в относительной сложности выражений, связывающих их с параметрами системы.

4. Частотные методы оценки показателей качества.

С помощью полученных вещественных или мнимых частотных характеристик можно определять показатели качества САР. Для этого существует два способа оценки качества: по виду вещественной частотной характеристики (ВЧХ) и по номограмме В.В. Солодовникова.

Если комплексная передаточная функция замкнутой САР имеет вид:

, - ВЧХ, - мнимая частотная характеристика, то справедливо отношение: …(2.32).

Данная зависимость часто позволяет уже по виду и параметрам ВЧХ судить о качестве переходного процесса. Рассмотрим некоторые свойства ВЧХ.

1. Изменение масштаба по оси ординат. Если изменить масштаб по оси ординат ВЧХ в n раз, то масштаб кривой переходного процесса изменится в то же число раз. Для доказательства этого свойства достаточно умножить правую и левую части уравнения (2.32) на n. Это свойство иллюстрируют графики, показанные на рис. 2.17 а и б.

2. Изменение масштаба по оси абсцисс. Если увеличить в n раз масштаб аргумента ВЧХ, то масштаб кривой переходного процесса уменьшится в то же число раз. Это свойство иллюстрируют графики, показанные на рис. 2.17 а и 2.18.

3. Установившееся значение переходного процесса. Согласно теореме о конечном значении можно записать:

4. Начальное значение переходного процесса. Согласно теореме о начальном значении можно записать:

.

5. Если ВЧХ может быть представлена суммой характеристик, то переходная характеристика также представляет собой сумму: ;

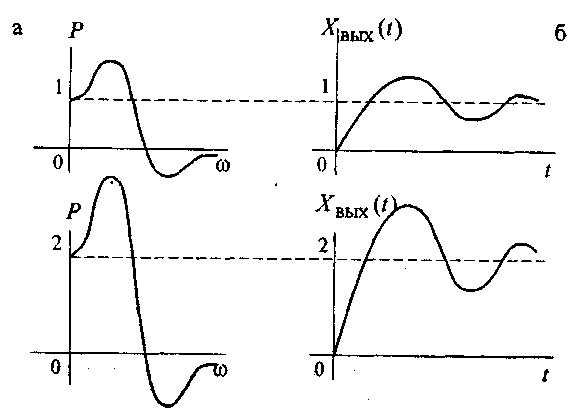
Рис. 2.17. Изменение масштаба по оси ординат: а) – начальные ВЧХ и ;

б) – увеличенные в 2 раза ВЧХ и .

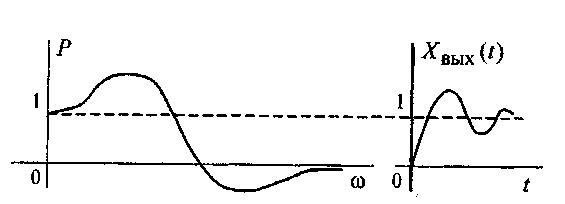
Рис. 2.18. Изменение масштаба по оси абсцисс.

5. Метод построения переходного процесса с помощью трапецеидальных характеристик.

Наибольшее распространение получил метод В.В. Солодовникова, который ввел в рассмотрение единичные трапецеидальные частотные характеристики, имеющие следующие показатели: высота , интервал равномерного пропускания частот , интервал пропускания частот ( - частота среза), коэффициент наклона . Типовая единичная трапеция показана на рис. 2.19 а, а типовая ВЧХ - на рис. 2.19 б.

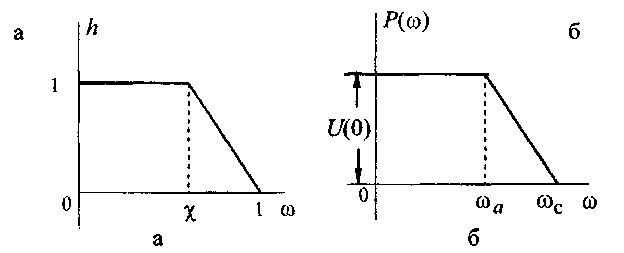
Рис. 2.19. Типовые характеристики: а) - единичная трапеция; б) - типовая ВЧХ.

Единичная трапеция при , полностью характеризуется коэффициентом наклона. Для таких единичных трапеций при произведен по выражению (2.32) расчет единичных переходных функций.

Реальную ВЧХ аппроксимируют суммой неединичных трапецеидальных характеристик. Для каждой неединичной характеристики, пользуясь таблицей h-функций, находят переходную характеристику. По коэффициенту наклона i-й трапеции выписывают значения единичной переходной функции , а затем производят перерасчет для неединичной по формулам: ; .

Переходная характеристика системы находится, как алгебраическая сумма неединичных переходных функций: , где m - число трапеций.