§ 6.4. Критерии устойчивости. Аналитические критерии устойчивости.

Далеко не всегда бывает удобно вычислять корни характеристического уравнения. В теории автоматического управления и регулирования существует достаточно много методов определения знака вещественной части корней характеристического уравнения по значениям его коэффициентов без нахождения самих корней. Эти методы и называются критериями устойчивости.

Критерий устойчивости - это математически сформулированные условия, которым должны удовлетворять коэффициенты характеристического уравнения или какие-либо функции этих коэффициентов, чтобы система была устойчивой.

1. Необходимое условие устойчивости.

Покажем, что необходимым (но недостаточным) условием устойчивости системы является положительность всех коэффициентов характеристического уравнения. Это значит, что при положительности всех коэффициентов система м.б. устойчивой, но не исключена возможность неустойчивости системы. Если же не все коэффициенты характеристического уравнения положительны, то система наверняка неустойчива и никаких дополнительных исследований устойчивости не требуется.

Заметим, что вместо того, чтобы быть положительными, все коэффициенты характеристического уравнения м.б. отрицательными. Умножая все члены характеристического уравнения на минус единицу, можно сделать все коэффициенты положительными, т.е. в этом случае выполнить указанное выше требование.

Для доказательства необходимого условия устойчивости будем вначале предполагать, что все корни вещественные. Представим левую часть характеристического уравнения (5, § 6.4) в виде произведения , где - корни характеристического уравнения. При этом будем считать, что . Это всегда можно выполнить умножением уравнения на минус единицу.

В устойчивой системе все корни д.б. отрицательными, т.е. и т.д. При этом получим .

Если теперь раскрыть скобки и вернуться к уравнению вида (5.5.9), то все коэффициенты уравнения получатся положительными, т.к. перемножая и складывая положительные величины и т.д., нельзя получить отрицательных величин.

При наличии в решении характеристического уравнения комплексных корней с отрицательной вещественной частью, например, , результат не изменится, т.к. множители, соответствующие этим корням, будут иметь вид:

.

Очевидно, что появление такого множителя не может изменить вывод о положительности всех коэффициентов характеристического уравнения.

Имея ввиду рассмотренное выше необходимое условие устойчивости, далее будем предполагать, что все коэффициенты характеристического уравнения положительны.

Необходимое условие устойчивости становится достаточным только для уравнений первого и второго порядков. В этом случае система будет устойчивой при положительности всех коэффициентов характеристического уравнения, в чем нетрудно убедиться прямым нахождением корней уравнения.

Все критерии устойчивости можно разделить на две группы: аналитические и частотные. Рассмотрим наиболее широко применяемые критерии обеих групп.

2. Аналитические критерии устойчивости.

К этой группе относятся критерии, которые позволяют проверить устойчивость аналитическими вычислениями над коэффициентами характеристического уравнения. Они еще часто называются алгебраическими.

2.1. Критерий устойчивости Вышнеградского.

Русским математиком И.А. Вышнеградским в 1876 году было определено условие устойчивости САР, описываемой линейным дифференциальным уравнением третьего порядка. Характеристическое уравнение будет иметь вид:

…(1).

Разделим уравнение (1) на . В результате имеем:

…(2),

где ; ; ; ; .

Перейдем к безразмерному параметру , приняв . Тогда получим уравнение Вышнеградского: …(3).

Условие обеспечения устойчивости системы третьего порядка Вышнеградский определил неравенством или . Предельное условие устойчивости определяется при или уравнением гиперболы, построенной в плоскости координат и как это показано на рис. 2.5.

Кривая границы устойчивости делит плоскость на две области - область устойчивости ( ) и область неустойчивости ( ). Область устойчивости в зависимости от взаимного расположения корней характеристического уравнения может быть разделена на три подобласти, каждой из которых соответствует определенный вид переходного процесса.

По графику областей устойчивости можно для САР третьего порядка по заданным параметрам определить вид переходной характеристики или, наоборот, по желаемому виду переходного процесса подобрать тот или иной параметр системы.

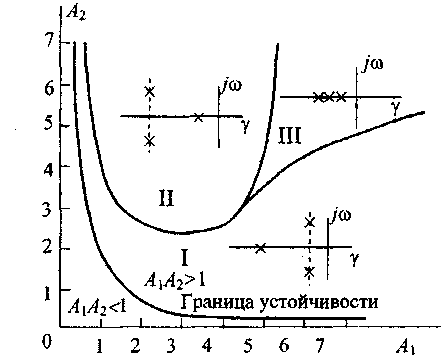
Рис. 2.5. Диаграмма И.А. Вышнеградского.

2.2. Критерий устойчивости Гурвица.

Задача отыскания критерия устойчивости для систем, описываемых ДУ любого порядка, была сформулирована Максвеллом в 1868 году. Эта задача была впервые решена в алгебраической форме Раусом в 1873 году для уравнений четвертой и пятой степени и в 1877 году – полностью.

Поскольку критерий Рауса дан в форме алгоритма, определяющего последовательность математических операций, необходимых для решения задачи, использование его в практике является неудобным.

Поэтому большее распространение получил алгебраический критерий устойчивости, сформулированный в 1885 году математиком А. Гурвицем. Этот критерий был найден Гурвицем по просьбе словацкого профессора Стодолы, занимавшегося исследованием процесса регулирования турбин. Ниже критерий Гурвица приводится без доказательства.

Для характеристического уравнения …(4) составим квадратную матрицу (таблицу) коэффициентов, содержащую n строк и n столбцов:

…(5).

Эта таблица составляется следующим образом.

По диагонали от верхнего до правого нижнего углов выписываются все коэффициенты по порядку от до . Каждая строка дополняется коэффициентами с возрастающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента, а также, если индекс его меньше нуля или больше n, на месте его пишется нуль.

Критерий устойчивости сводится к тому, что при д.б. больше нуля все n определителей, называемых определителями Гурвица, получаемых из квадратной матрицы по следующему правилу:

…(6), …(7), ,…(8),…..

Последний определитель включает в себя всю матрицу. Но т.к. в последнем столбце все элементы, кроме нижнего, равны нулю, то последний определитель Гурвица выражается через предпоследний следующим образом: …(9).

Однако в устойчивой системе предпоследний определитель тоже д.б. положительным. Поэтому условие положительности последнего определителя сводится к условию , т.е. к положительности свободного члена характеристического уравнения.

Условия нахождения на границе устойчивости можно получить, приравнивая нулю последний определитель , при положительности всех остальных определителей. Как следует из (9), это условие распадается на два условия: и . Первое условие соответствует границе устойчивости первого типа (апериодическая граница устойчивости) и второе – границе устойчивости второго типа (колебательная граница устойчивости).

Раскрывая определители, фигурирующие в общей формулировке критерия устойчивости Гурвица, можно получить в виде частных случаев критерия устойчивости для системы первого, второго, третьего, четвертого и более высоких порядков.

1. Уравнение первого порядка: .

Для этого уравнения критерий Гурвица дает , т.е. коэффициенты характеристического уравнения д.б. положительными.

2. Уравнение второго порядка: .

Для этого уравнения критерий Гурвица требует . Последний определитель, как отмечалось выше, сводится к условию положительности последнего коэффициента: . Таким образом, и для уравнения второго порядка необходимым и достаточным условием устойчивости является положительность всех коэффициентов характеристического уравнения.

3. Уравнение третьего порядка: .

Для этого уравнения получаем условия:

. Условие при положительных может выполняться только при .

Следовательно, для уравнения третьего порядка уже недостаточно положительности всех коэффициентов характеристического уравнения. Требуется еще выполнение определенного соотношения между коэффициентами: .

4. Уравнение четвертого порядка: .

На основании критерия Гурвица можно получить, что для уравнения четвертого порядка, кроме положительности всех коэффициентов, требуется выполнение условия:

.

5. Уравнение пятого порядка: .

Для уравнения пятого порядка, кроме положительности всех коэффициентов, должны выполняться еще два условия:

, .

Как видно, уже для уравнения пятой степени условия устойчивости по критерию Гурвица получаются достаточно громоздкими. Поэтому использование этого критерия практически ограничивается уравнениями четвертого порядка.

Существенным недостатком критерия Гурвица является также то, что для уравнений высоких порядков в лучшем случае можно получить ответ о том, устойчива или неустойчива система АР.

При этом в случае неустойчивости системы критерий не дает ответа на то, каким образом надо изменить параметры системы, чтобы сделать её устойчивой. Это обстоятельство привело к поискам других критериев, которые были бы более удобными в инженерной практике.