Тема 6. Устойчивость и качество сау (16).

§ 6.1. Устойчивость динамических систем. Общие определения и понятия.

Для выполнения любых практических задач управления и регулирования система должна быть устойчивой.

Устойчивость - это свойство системы возвращаться в исходный или близкий к нему установившийся режим после выхода из него в результате какого-либо воздействия.

Если САР не может восстановить первоначальный режим, то такой переходный процесс называется расходящимся, а система - неустойчивой.

Неустойчивый переходный процесс может иметь характер колебаний с возрастающей амплитудой, как показано на рис. 2.1 б, или он может монотонно возрастать, как это показано на рис. 2.1 а.

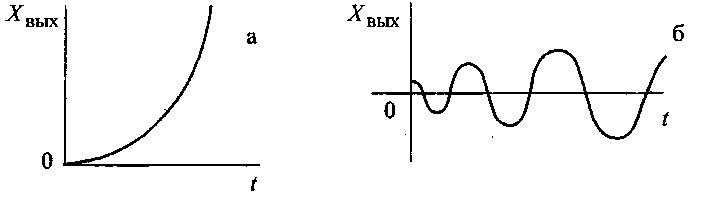
2.1. Неустойчивый переходный процесс: а) – монотонный; б) – колебательный.

Если САР восстанавливает первоначальный режим, то такой переходный процесс называется сходящимся, а система - устойчивой. Виды устойчивых переходных процессов показаны на рис. 2.2, а и б.

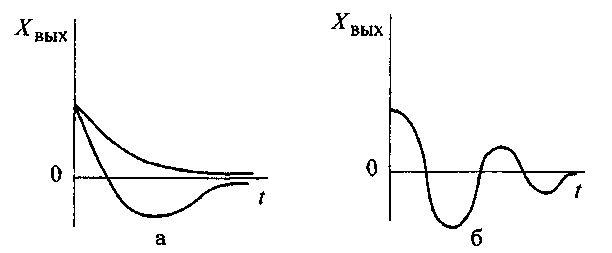
Рис. 2.2. Устойчивый переходный процесс: а) – монотонный; б) – колебательный.

Есть особый случай, когда система переходит в новое установившееся состояние, которое может иметь незатухающие колебания постоянной амплитуды (автоколебания) или монотонно перейти на другой постоянный уровень. Эти примеры иллюстрируются на рис. 2.3. Такие системы называются нейтральными. Для суждений об их устойчивости нужны дополнительные исследования. В теории автоматического управления разработаны математические методы исследования устойчивости. Основой такого исследования являются дифференциальные уравнения, описывающие поведение САР.

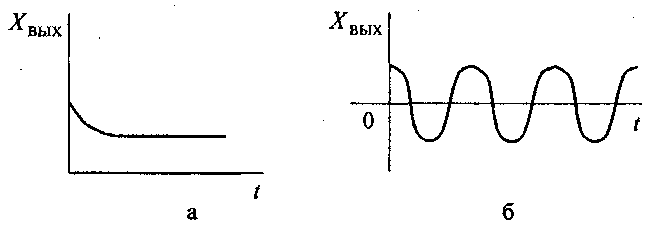
Рис. 2.3. Нейтральный переходный процесс: а) – монотонный; б) – колебательный.

При исследовании устойчивости системы наиболее очевидным представляется прямой метод, который предполагает построение переходного процесса путем решения исходных уравнений САР относительно регулируемого параметра . По виду полученного решения и судят об устойчивости (или неустойчивости) системы.

Прямой метод исследования устойчивости обладает двумя существенными трудностями, а именно: во-первых, реальные САР являются нелинейными или имеют распределенные параметры, что значительно усложняет получение точного аналитического решения; во-вторых, для линейных или линеаризованных систем, описываемых уравнениями выше четвертого порядка, получить решение в конечном виде в общем случае невозможно. Частные же численные решения уравнений динамики САР не позволяют получить общего представления о поведении системы во всем возможном диапазоне изменения параметров.

§ 6.2. Теоремы Ляпунова об устойчивости сау линейного приближения.

Обычно, в качестве первого шага, исследование устойчивости реальной системы заменяется исследованием ее линейного приближения. При этом возникает проблема адекватности линейного приближения и реальной САР, т.е. можно ли судить об устойчивости реальной системы по устойчивости ее линейного приближения. Ответ на этот вопрос дает теория устойчивости движения динамических систем, созданная русским ученым A.M. Ляпуновым. Три теоремы, сформулированные и доказанные им, позволяют судить об устойчивости систем по первому приближению, в области малых отклонений регулируемого параметра, т.е. по линеаризованным уравнениям. Практически это означает, что для решения задачи устойчивости достаточно исследовать переходный процесс при бесконечно малом отклонении системы от базового положения равновесия.

Теорема 1. Если вещественные части всех корней характеристического уравнения системы первого приближения (линеаризованной системы в области отклонений регулируемого параметра) отрицательны, то нулевое решение исходной системы асимптотически устойчиво независимо от членов разложения выше первого порядка.

Теорема 2. Если среди корней характеристического уравнения системы первого приближения имеется хотя бы один с положительной вещественной частью, то нулевое решение исходной системы дифференциальных уравнений неустойчиво независимо от членов разложения выше первого порядка.

Теорема 3. Если среди корней характеристического уравнения первого приближения есть нулевые, то в этом случае для суждения об устойчивости нулевого решения исходной системы необходимо учитывать члены выше первого порядка.

Важная заслуга A.M. Ляпунова заключается в том, что ему удалось найти подход к определению свойства устойчивости, который базируется на очень простой идее, известной из механики, а именно: в положении равновесия любая динамическая система имеет минимум потенциальной энергии.

Известно, что минимум потенциальной энергии всегда можно считать равным нулю. Тогда в любой окрестности положения равновесия потенциальная энергия будет положительной. Применение функций, которые положительны всюду, за исключением положения равновесия, к анализу устойчивости и лежит в основе метода, разработанного A.M. Ляпуновым. Они названы функциями Ляпунова. Единого способа формирования функции Ляпунова для анализа конкретных САР не существует.

Наглядно устойчивость равновесия иллюстрируется рис. 5.1, а, на котором изображен шар, лежащий в некотором углублении. При всяком его отклонении от положения равновесия он будет стремиться возвратиться к нему точно (при отсутствии сил трения) или к некоторой конечной области, окружающей предшествующее положение равновесия (при наличии сил трения). Такое положение шара будет устойчивым.

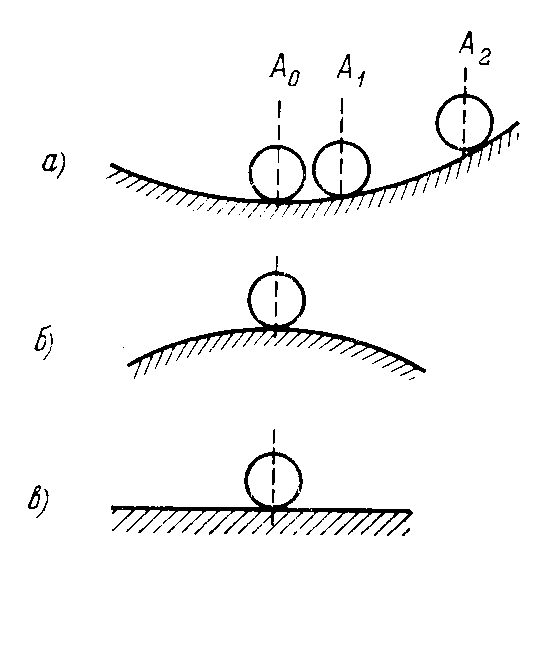
Рис 5.1.

На рис 5.1, б изображен другой случай, когда положение шара оказывается неустойчивым. Рис. 5.1, в соответствует случаю безразличного положения равновесия.

Понятие устойчивости можно распространить и на случай движения некоторой системы. Пусть её состояние определяется независимыми координатами . Заданное движение системы определяется некоторым законом изменения координат: .

Аналогично случаю равновесия, заданное движение можно назвать невозмущенным движением. Приложение внешних сил к рассматриваемой системе вызовет отклонение действительного движения от заданного: и т.д. Это движение будет возмущенным.

Заданное невозмущенное движение будет устойчивым, если в результате приложения внешних сил, которые затем снимаются, возмущенное движение по истечении некоторого времени войдет в заданную область: , .

Данное выражение является близким к строгому понятию устойчивости, введенному русским математиком А.М. Ляпуновым.