Ентропія. Властивості ентропії

Ентропія визначає міру невизначеності всієї безлічі повідомлень на вході каналу і обчислюється як середня кількість власної інформації у всіх повідомленнях:

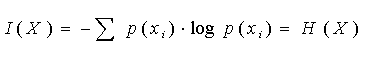(5)

Властивості ентропії:

1. Ентропія H(X) ненегативна: H(X) > 0.

2. Ентропія H(X) < logN.

3. Величина logN = D називається інформаційною пропускною спроможністю алфавіту (інформаційною місткістю алфавіту).

4. Якщо N = 2, то p(x₁) = p, p(x₂) = 1p,

H(Х)= - p log p – (1p) log (1p).

5. Найвища невизначеність, а відтак і максимум ентропії досягається при p = 0,5 і тоді

H(Х) = -log 0,5 = log 2 = 1,

тобто місткість двійкового алфавіту дорівнює 1 біт.

Залежність H(X) від величини р показано на рис. 7.

6. Ентропія для об’єднаних ансамблів:

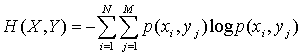. (6)

7. Часткова умовна ентропія

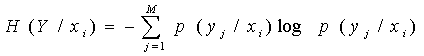. (7)

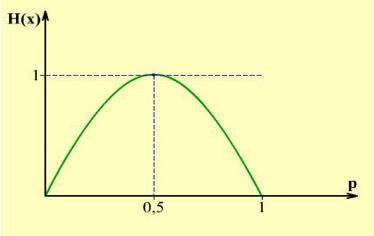
1. Залежність h(X) від величини р

Середнє значення часткових умовних ентропій називається умовною ентропією

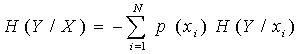. (8)

Вона характеризує невизначеність результату подій у при відомих подіях х.

Якщо врахувати, що математичне очікування є результат усереднювання по всіх станах, то вирази (5), (6) і (8) можна записати у вигляді

,

,

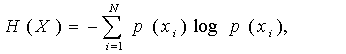
де М – математичне очікування. З теорії ймовірності відомо, що

p(x, у) = p(x) p(у/x) = p(y) p(x/y).

Після логарифмування і застосування операції пошуку математичного очікування одержуємо співвідношення:

H(X,Y) = H(X) + H(Y/X),

H(X,Y) = H(Y) + H (X/Y). (9)

У іншій формі (9) має вигляд

H(X)  H (X/Y) = H(Y)  H (Y/X). (10)

Ліву частину (10) можна інтерпретувати як середню кількість інформації I(X, Y), доставлену в пункт прийому, яка дорівнює середній кількості переданої інформації H(X) мінус середню кількість інформації H (X/Y), втрачену унаслідок дії шумів:

I(X, Y) = H(X)  H (X/Y).

Права частина (10) містить ентропію шуму H(Y/X) при відомому сигналі X:

H(Y/X) = H(Y)  H (Y/X).

Обидві частини рівності (10) однаково придатні для визначення середньої кількості переданою по каналу інформації.

Ентропія систем з безперервною безліччю станів обчислюється за правилами аналізу дискретних систем з попереднім квантуванням щільності ймовірності w (x) з кроком Δх.

Тоді число станів в системі буде дорівнювати

,

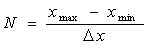а ймовірність станів p(x_i)= w (x_i) Δх.

Використовуючи відомі формули даного розділу, можемо одержати ентропію

.

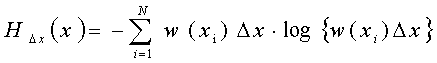Після перетворень і устремління Δх до нуля одержуємо

(11)

Величина H*(X) називається приведеною ентропією. Вона дорівнює:

(12)

31. Інформаційні характеристики неперервних повідомлень. Епсілон- ентропія.

Джерело безперервних повідомлень характеризується тим, що в кожний момент часу повідомлення може приймати безліч значень з нескінченно малою ймовірністю кожного і них, і, якщо б повідомлення могло передаватися абсолютно точно без спотворень, воно несло б нескінченна кількість інформації. Однак на практиці при передачі інформації завжди мають місце спотворення і кількість інформації, що міститься в прийнятому безперервному повідомленні, визначається різницею значень ентропій повідомлення до і після отримання інформації. Ця різниця є кінцевою величиною. Нехай - Реалізація безперервного повідомлення на вході каналу зв'язку, - Реалізація вихідного повідомлення; - Одномірна щільність ймовірності вхідних повідомлень, - Умовна щільність ймовірності х при відомому у (Апостеріорна ймовірність); - Умовна щільність ймовірності у при відомому х, - Спільна щільність ймовірності. Тоді будуть мати місце такі вирази:

1. Ентропія джерела безперервних повідомлень: 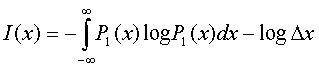, де 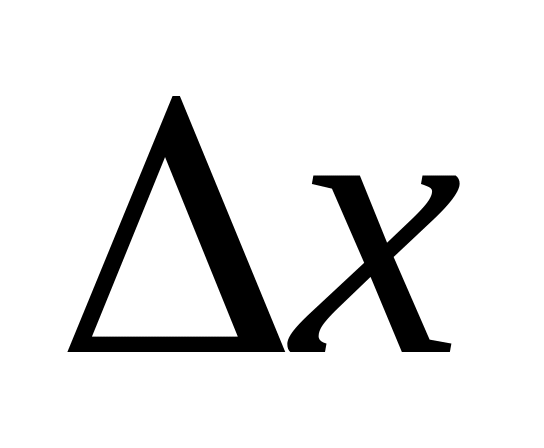- Інтервал квантування (точність вимірювання);

2. Диференціальна ентропія джерела безперервних повідомлень:

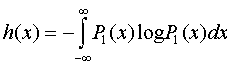
Визначальна кількість інформації в бітах, що припадає в середньому на один відлік.

3. Максимальна диференціальна ентропія джерела безперервних повідомлень:

Яка має місце при нормальній щільності розподілу випадкового процесу:

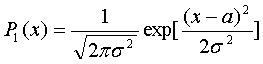
- Математичне сподівання випадкової величини,

- Дисперсія цієї величини,

• - Основа натурального логарифма.

3. Повна середня взаємна інформація:

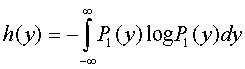- Диференційна ентропія повідомлення на виході каналу зв'язку:

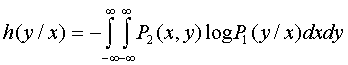
диференціальна умовна ентропія, яка характеризує шумового процесу.

4. Для адитивної суміші 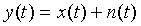при статистичній незалежності нормальних процесів і перешкоди :

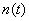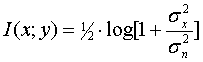
де і - Відповідно дисперсії процесів і .

6. Пропускна здатність каналу зв'язку для нормально розподілених повідомлення і перешкоди:

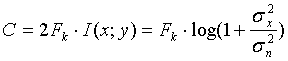, (Біт / с)

де - Смуга пропускання каналу.

7. Пропускна здатність каналу зв'язку при :

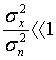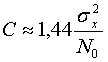, (Біт / с)

де - Спектральна щільність адитивної перешкоди.

8. Пропускна здатність каналу зв'язку при спектральної щільності гауссовского сигналу і спектральної щільності адитивної гауссовой перешкоди визначається:

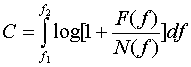
де - Ефективна смуга частот, займана інформаційним сигналом, .

Епсилон -ентропія (ε-энтропия )

Безперервні сигнали сприймаються з обмеженою точністю. Нехай Х - точний сигнал, його щільність ймовірності w (x). Сигнал, відтворений будь апаратурою, відрізняється від вихідного сигналу. Тобто, на виході апаратури маємо інший сигнал Y, відмінний від X. Критерієм близькість двох сигналів X і Y є функціонал:

де h (x, y) - деяка вагова функція, яка має природу відстані.

Функціонал F за своїм виглядом являє собою математичне сподівання функції h (x, y) випадкових аргументів x і y. Якщо підібрати відповідним чином цю функцію, то як критерій близькості двох сигналів можна використовувати умову , де – деяка наперед задана величина. Зазвичай використовують середньоквадратичної критерій

Сигнал Y містить інформацію щодо X у відповідності з виразом

Ентропія H (X) визначається функцією w (x), яка є заданою. Варіюючи функцію w (x / y) можна в принципі домогтися мінімального значення величини при заданих вимогах до точності .

, при обмеженні

Таким чином, ε-ентропія величини X називається мінімальна кількість інформації в одній випадкової величини Y відносно іншої X, при якому задовольняється заданий вимога до вірності відтворення величини X.