30. Інформаційні параметри повідомлень та сигналів. Поняття ентропії.

При введенні кількісної міри інформації було прийнято смисловий зміст повідомлень (семантику) не враховувати, а обмежитися тільки формальними ознаками, важливими з погляду передачі повідомлень по каналах зв’язку. У результаті враховуються тільки число N повідомлень, що підлягають передачі, і ймовірності р(х_i) надходження їх на вхід каналу. Всю сукупність повідомлень представляють у вигляді деякої системи Х із станами x_i

, (1)

де: x_i – окремі повідомлення (або їх типи, класи), p(x_i) – апріорна ймовірність появи повідомлень x_i.

В результаті передачі повідомлення x_i по каналу зв’язку буде одержане повідомлення y_j. Воно може з деякою ймовірністю бути схоже на будь-яке з (x₁, x₂,…x_N) повідомлень. Зокрема воно може бути схоже на передане повідомлення xi. Апостеріорна (післядослідна) ймовірність присутності x_i в y_j дорівнює p(x_i/ y_j).

У основу міри кількості інформації встановлені зміни ймовірності появи повідомлень від апріорного значення p (x_i) на вході каналу до апостеріорного значення p (xi/yj) на виході каналу, пов’язані із викривленнями інформації у каналі.

Порівнюючи ймовірність р(x_i) і p (x_i/y_j) можна встановити міру кількості інформації, переданої через даний канал. Зручною мірою виявився логарифм відношення апостеріорної ймовірності до апріорної.

Кількість інформації, те, що міститься в події y_j щодо події x_i визначається по формулі:

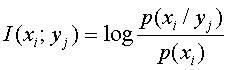
Основою логарифма можуть бути: 2, е  2,72, або 10. Залежно від основи міняються одиниці вимірювання кількості інформації (біти  дв. од.; ніт  нат. од.; хартлі (діти)  дес. од.)

Властивості кількості інформації I(x_i; y_i):

1. Властивість симетрії.

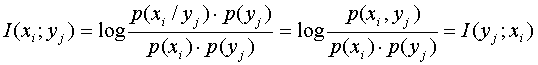
2. Властивість адитивності.

.

Середня кількість взаємної інформації виходить шляхом усереднювання (2) по всіх i і j :

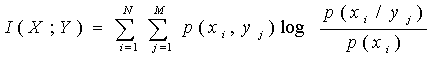
1. Властивість симетрії. Інформація, що міститься в y_j щодо x_i, дорівнює інформації, що міститься в x_i щодо y_j. Це стає очевидним, якщо чисельник і знаменник в (1) помножити на p (yi) і виробити перетворення:

,

оскільки p (x_i, y_j) = p (y_j), p(x_i/ y_j) = p (x_i), p (y_j/ x_i) - ймовірність сумісної появи y_j і x_i.

В результаті вказаної властивості величину I(x_i;y_j) називають кількістю взаємної інформації між x_i і y_j.

2. Властивість адитивності. Інформація, що міститься в парі символів y_j, z_k щодо x_i, дорівнює сумі інформації, що міститься в y_j щодо x_i і інформації, що міститься в z_k щодо x_i за умови, що значення y_j відоме

. (3)

Кількість власної інформації у x_i визначається з (2) при p(x_i/ y_j) = 1

. (4)

Ця величина визначає кількість інформації, необхідне для однозначного визначення xi на виході каналу.

З урахуванням введеного поняття (4) можна перетворити вираз (2) до вигляду

,

де I (x_i / y_j) = -log p (x_i / y_j)  умовна власна інформація.

Середня кількість взаємної інформації виходить шляхом усереднювання (2) по всіх i і j :

.