29. Оптимальний когерентний прийом цифрових сигналів.

У задачі розпізнавання сигналів, що не містять випадкових параметрів (тобто точно відомих), «причинами» є надходження на вхід сигналів , ймовірності яких рівні, очевидно, імовірності появи відповідних елементів . «Наслідками» є реалізації суми сигналу і перешкоди.

Кількісно опис ситуації зручно проводити за допомогою розгляду векторів відповідних коливань. замість сигналів будем оперувати однозначно відповідними їм векторами , а замість реалізацій y (t) - векторами , координати яких визначаються виразом, який в нашому випадку запишемо так:

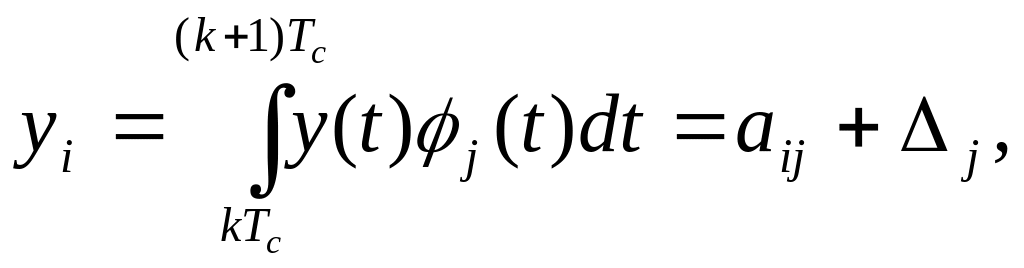(1)

Відповідно до теореми Байеса:

(2)

Як було зазначено, рішення зазвичай виноситься на користь сигналу, що має найбільшу апостеріорну ймовірність. Так як знаменник не залежить від номера I, то вирішальне правило (алгоритм рішення) визначається так:

(3)

Слід звернути увагу на те, що в цих висловах -- щільності ймовірностей, так як компоненти вектора y, як видно з (1), є безперервними випадковими величинами.

У виразі (3) апріорні ймовірності передачи елементів повинні бути задані. Отже, необхідно визначити тільки правдоподібності . Це можна зробити виходячи з того, що перешкода аддитивна. так як

,

то щільність ймовірності деякого значення вектора дорівнює щільності ймовірності, що вектор перешкоди n набуде значення . Звідси випливає, що якщо - відома нам щільність ймовірності вектора перешкоди, то

(4)

Останній перехід справедливий тому, що сигнал і перешкоди - незалежні процеси.

Для подальшої конкретизації алгоритму необхідно задати певний вид перешкоди. У більшості випадків мають місце нормальні (гаусові) або близькі до них перешкоди. Обчислення в цьому випадку виявляються найбільш простими. При гауссовских перешкодах кожна компонента вектора розподілена по нормальному закону

(5)

У ряді випадків, зокрема, при рівномірному розподілі енергії перешкоди по смузі розглянутих частот, компоненти вектора є незалежними випадковими величинами. Тоді, як відомо,

(6)

При залежних компонентах вираз для істотно ускладнюється і цей випадок тут розглядати не будемо.

Зазначимо, що , тобто є квадратом довжини (норми) вектора перешкоди.

Отже,

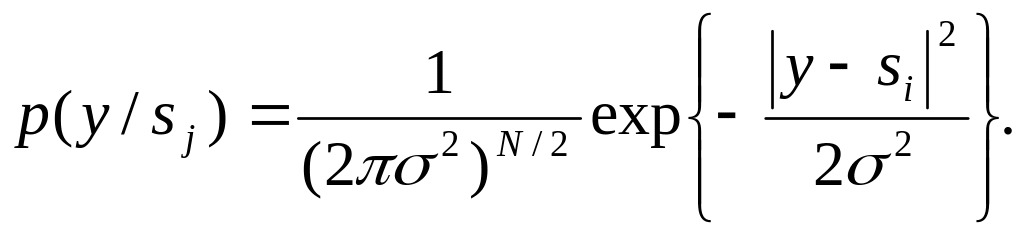(7)

Відкинувши множники, не залежні від номера сигналу i, вирішальне правило (3) можна представити у вигляді

(8)

Приймач, що працює за алгоритмом (8), називається байєсовський або приймачем максимальної апостеріорної ймовірності. Якщо апостеріорні ймовірності елементів однакові, то вирішальне правило спрощується:

(9)

Відповідний приймач називається приймачем максимального правдоподібності. Правило (9) розкриває механізм роботи оптимального приймача.

Отримавши вектор y, за допомогою обробки реалізації y (t) необхідно обчислити відстань від його кінця до кінців векторів всіх можливих сигналів і винести рішення на користь того сигналу, для якого величина буде мінімальною, тому що саме в цьому випадку функція (9) досягне максимуму. Коротко можна сказати, що оптимальний приймач виносить рішення на користь сигналу «найближчого» до y (t).

Вираз (9) досягає максимуму при мінімумі показника експоненти. Отже, правило (9) можна записати в іншому вигляді:

або, враховуючи векторне уявлення

(10)

Тут перший член в дужках не залежить від номера i. Останній член - є енергія i-того сигналу. Якщо енергії всіх сигналів однакові, що зазвичай має місце, то цей член також не залежить від номера i. Таким чином, вирішальне правило можна записати так:

(11)

Справедливість такого переходу зумовлена ​​тим, що другий член в (10) має знак мінус і вираз (10) мінімізується, якщо цей член досягає максимуму. Вираз (11) вже дозволяє визначити структуру оптимального приймача. Однак зручніше це вираз представити в іншому вигляді. Дійсно, врахуємо, що

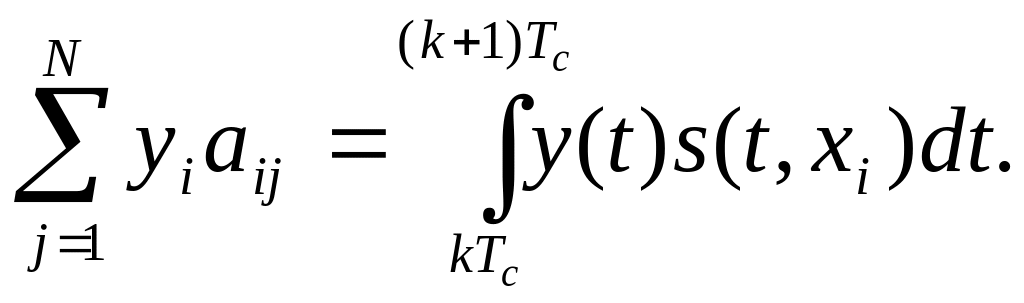(12)

Тоді остаточно отримаємо:

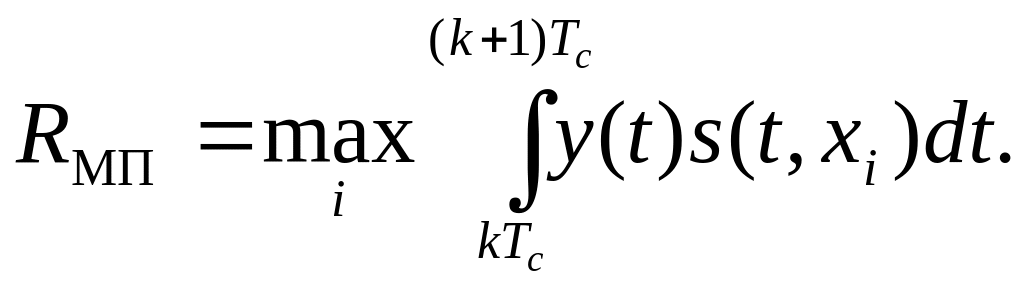(13)

Ця структура називається оптимальним кореляційним приймачем, так як основна операція, що лежить в його основі, це операція кореляції y(t) з усіма можливими сигналами .

З проведеного розгляду випливає, що до складу оптимального приймача повинні входити генератори, що виробляють зразки сигналів , тотожні тим, які використовуються на передавачі. Крім того, між роботою генераторів передавача і приймача повинна дотримуватися синхронність і синфазность, тобто забезпечуватися ідеальна синхронізація.