28. Оптимальний некогерентний прийом цифрових сигналів у гауссовому каналі.

Раніше було показано, що якщо імпульсний відгук лінії являє собою - функцію, то така лінія тільки послаблює передається сигнал, не змінюючи його форми. Нехай ослаблення сигналу а - повільно змінюється випадкова величина, практично постійна на інтервалах тривалістю Тс. Якби а була постійною і відомою величиною, то здійснювався б прийом точно відомих сигналів з ​​вирішальним правилом

(1)

При випадковому значенні а слід усереднити результат за законом розподілу р (а); тоді при равновероятностних сигналах вирішальне правило набуде вигляду:

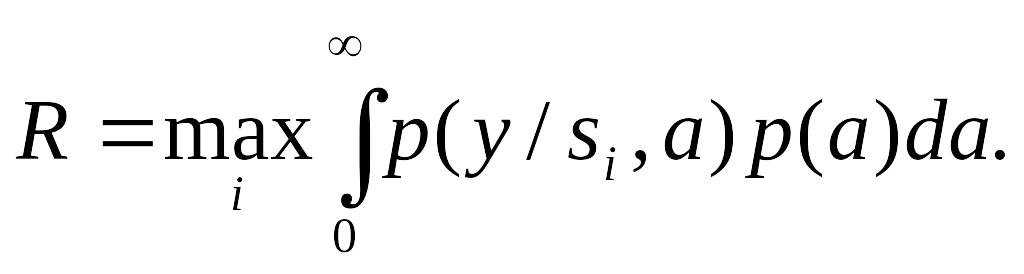(2)

Зі співвідношення (2) випливає, що при такому підході структура оптимального приймача залишиться колишньою (інваріантної до випадкових значень а). Імовірність же помилок (за інших рівних умов) зростає. При випадковому значенні а ці вирази необхідно усереднити по р. (а). Зокрема, для протилежних сигналів усереднене значення ймовірності помилки Р0ш має визначатися відповідно до виразом:

(3)

Для розподілу р (а), що підкоряється закону Релея можна показати, що:

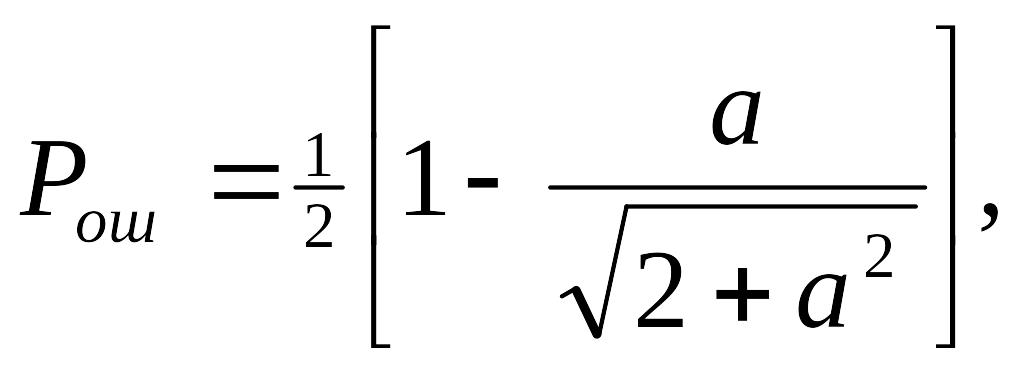(4)

де . Неважко бачити, що при однакових значеннях а ймовірність помилок, розрахована за формулою (4), значно перевищує імовірність помилок. Фізична причина збільшення ймовірності помилок ясна: зростання а призводить до деякого зменшення ймовірності помилок, однак падіння а призводить до значного зростання цієї імовірності внаслідок зазначеного вище «порогового ефекту».

Розглянемо далі випадок, коли лінія вносить до сигнали тільки випадковий зсув початкової фази, що має місце в переважній більшості реальних ситуацій. При цьому, якщо

то сигнали на виході лінії (вході приймача)

(5)

Вихідні сигнали (5) можна представити у вигляді двох складах з випадковими амплітудами, але постійними фазами:

(6)

де a і b можуть, на відміну від попереднього випадку, приймати і позитивні і негативні значення.

З (6) видно, що дія лінії можна звести до появи в точці прийому двох складових сигналу: косинусоїдальної і синусоїдальної. Аналіз цього випадку, пов'язаний з виконанням усереднення по обох випадковим параметрами a і b, досить громіздкий.

Наведемо кінцеве вираження для вирішального правила:

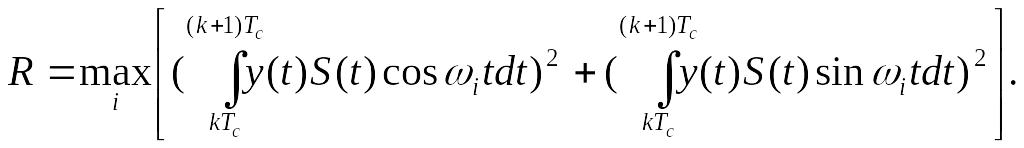(7)

З нього випливає, що оптимальний приймач виробляє кореляцію прийнятої реалізації у (t) зі зразками обох доданків сигналу. Зведення результатів у квадрати перед складанням і вибором максимуму викликано тим, що величини a і b можуть бути як позитивними, так і негативними.

Цей алгоритм можна реалізувати і за допомогою узгоджених фільтрів. Тут містяться детектори огинають вихідних коливань узгоджених фільтрів, після яких і проводиться відлік. Фізика процесів також ясна: якщо на вхід узгодженого з сигналом фільтра подати зрушений по фазі сигнал, то в силу лінійності фільтра відбудеться запізнювання коливання і на виході фільтра. Тому відлік в момент t = T_С не співпаде з максимумом напруги. У силу випадковості цього зсуву найкращою стратегією виявляється відлік обвідної, а не миттєвого значення коливання.

Порівняємо випадок прийому сигналів при відсутності випадкової фази (тобто точно відомих за формою сигналів) і при наявності випадкової фази. Перший випадок прийнято називати когерентним, а другий - некогерентним прийомом (саме цей випадок найчастіше має місце на практиці).

(8)

Порівнюючи вирази для когерентного і некогерентного прийому при однаковому значенні ймовірності помилки, можна встановити, який енергетичний програш дає застосування некогерентного прийому порівняно з когерентним. Розрахунки показують, що для забезпечення при некогерентном прийомі потрібне збільшення енергії сигналу на 15-30% в порівнянні з когерентним, тобто програш невеликий.

У більш загальному випадку неідеальність лінії обумовлює випадкові зміни амплітуди і фази. Ймовірність помилок від цього збільшується, тому що незалежно діють обидва розглянутих фактора. Можна показати, що в цьому випадку вірогідність помилок при розпізнаванні бінарних ортогональних сигналів дорівнює:

(9)

де - Середнє значення енергії прийнятих сигналів.