27. Потенціальна завадостійкість. Розрахунок імовірності помилки для різних сигналів.

З а визначенням В.А. Котельникова потенційної завадостійкістю називається максимум ймовірності правильного рішення, досяжний при заданих умовах прийому сигналів на тлі перешкод (шумів).Два сигнала та

Алгоритм прийняття рішення в приймачі:

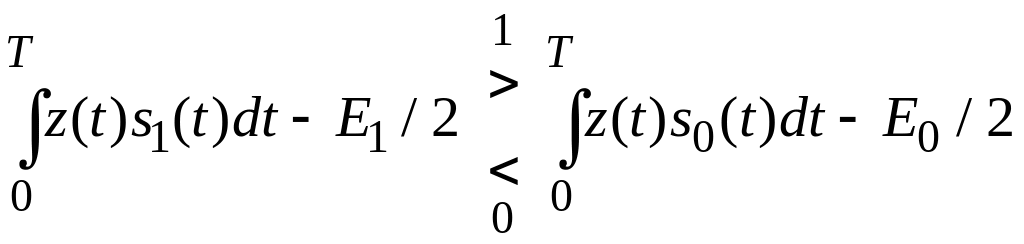
Або:

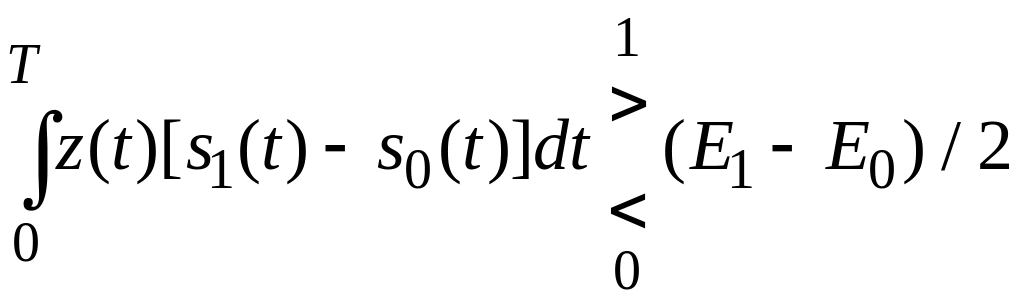
Прийняття рішення засноване на порівнянні з порогом деякої гауссовской с.в.

Помилки при прийомі полягають у тому, що при передачі першого сигналу приймається рішення про прийом другого і навпаки. Враховуючи, що гауссова розподіл симетрично і апріорні ймовірності рівні, легко бачити, що сумарна (середня) ймовірність помилки дорівнює будь-який з умовних ймовірностей помилок.

З найдемо умовну ймовірність помилки, то є ймовірність події, що полягає у прийнятті рішення про наявність сигнал за умови, що в спостережуваному коливанні присутній сигнал

Ця подія відповідає виконанню нерівності: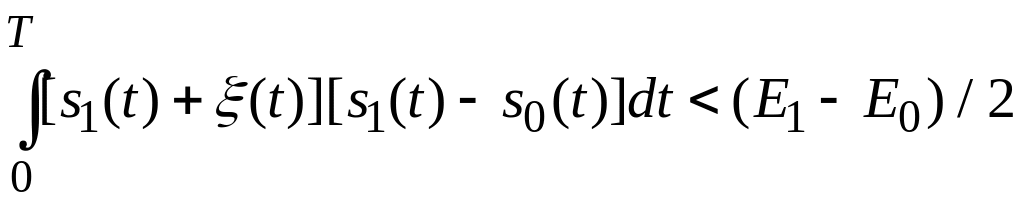

Перепишемо цей вираз:

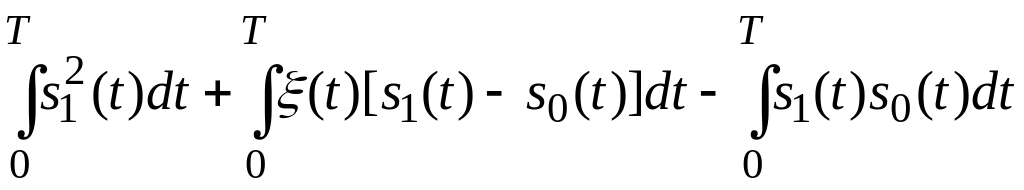
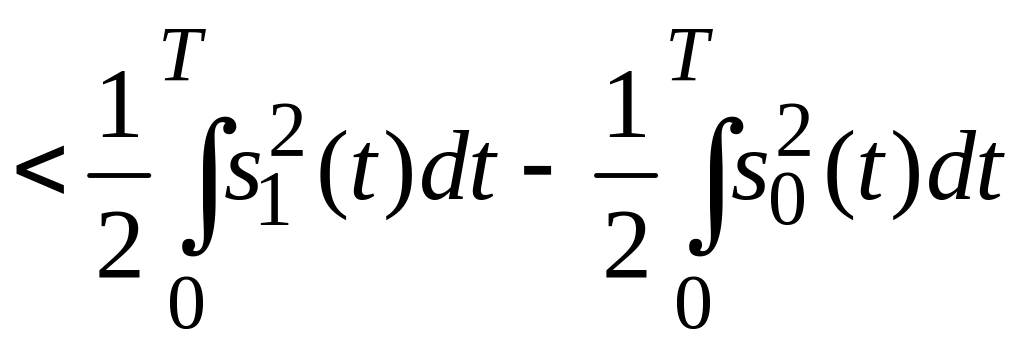
П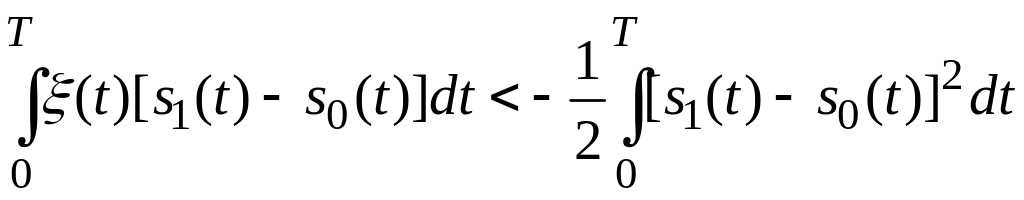 ісля очевидних перетворень отримаємо:

Б удемо називати різницевим сигналом:

Ліва частина нерівності:

являє собою випадкову величину, що має нормальний розподіл з нульовим середнім; позначимо її і знайдемо її середній квадрат, рівний дисперсії:

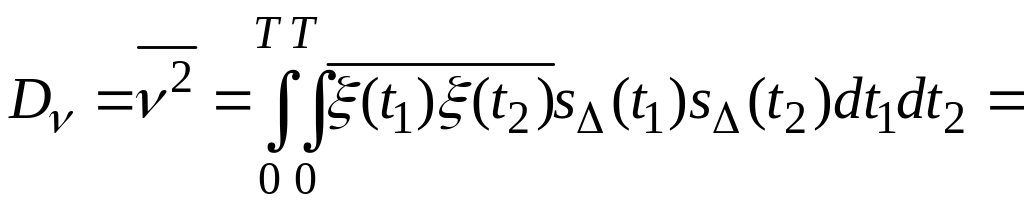
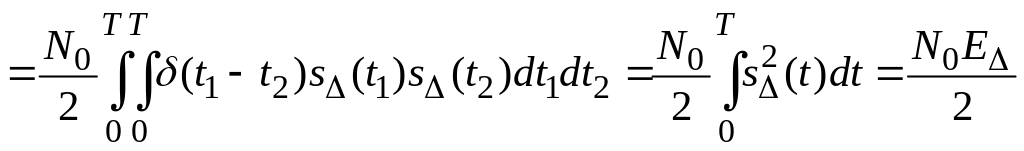
Цікавить нас ймовірність виконання нерівності:

– це ймовірність того, що нормальна випадкова величина з нульовим середнім і дисперсією

приймає значення менше, ніж .

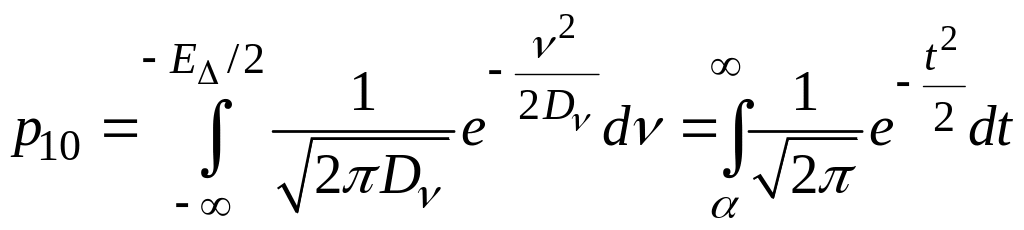
Ця ймовірність дорівнює:

д е – центрована нормальна випадкова величина з одиничною дисперсією,

– позитивне число.

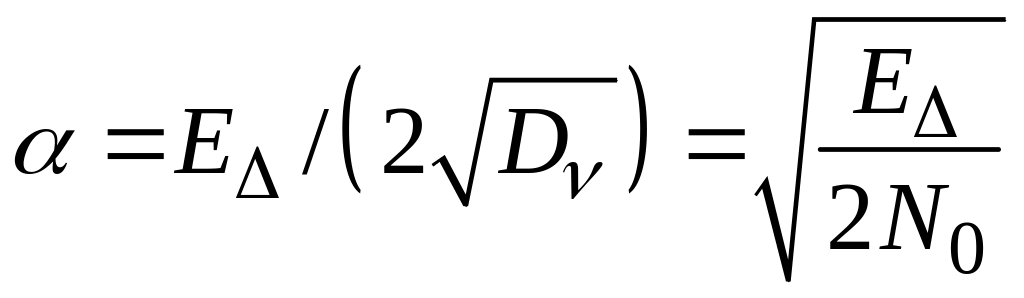
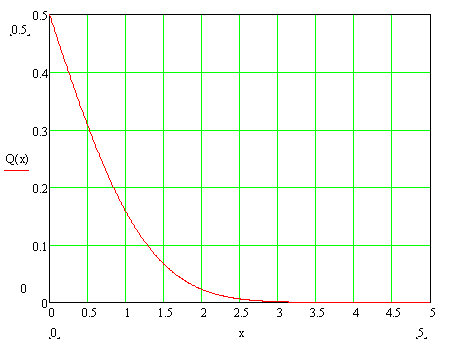
Очевидно, ймовірність залежить тільки від:

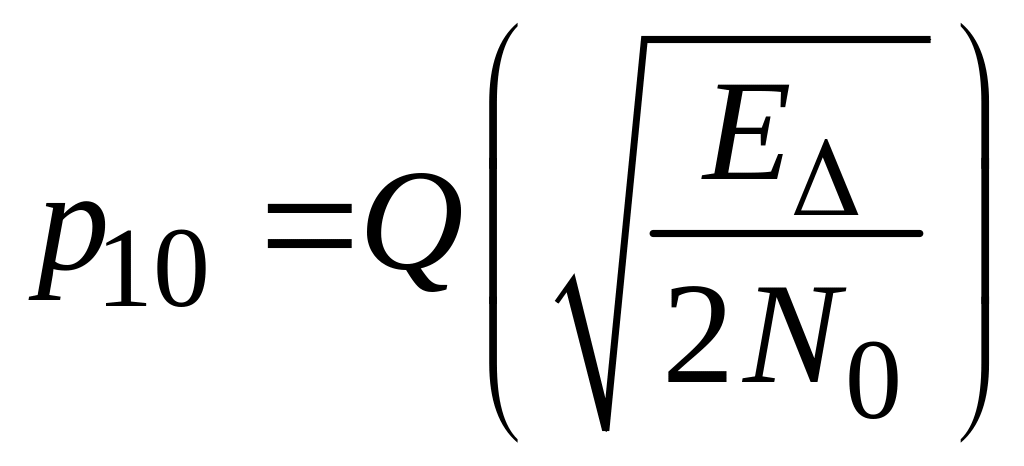
інтеграл ймовірності:

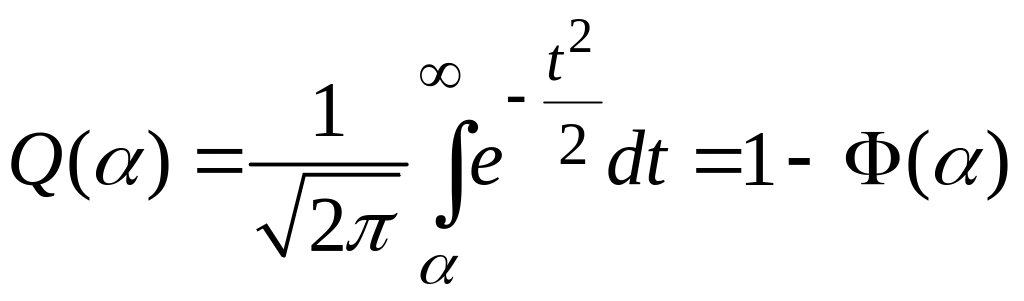
, інтеграл ймовірності

Таким чином, умовна ймовірність помилки,

рівна середньої ймовірності помилки при когерентному прийомі сигналів на фоні білого шуму, визначається енергією різницевого сигналу і спектральною щільністю потужності шуму.

Розглянемо потенційну завадостійкість двійкового когерентного приймача максимального правдоподібності для різних способів модуляції, вважаючи, що енергія посилки фіксована.

А мплітудна модуляція з пасивной паузою.

У цьому випадку та енергія різностного сигнала рівна (норма рівна ), рис. а

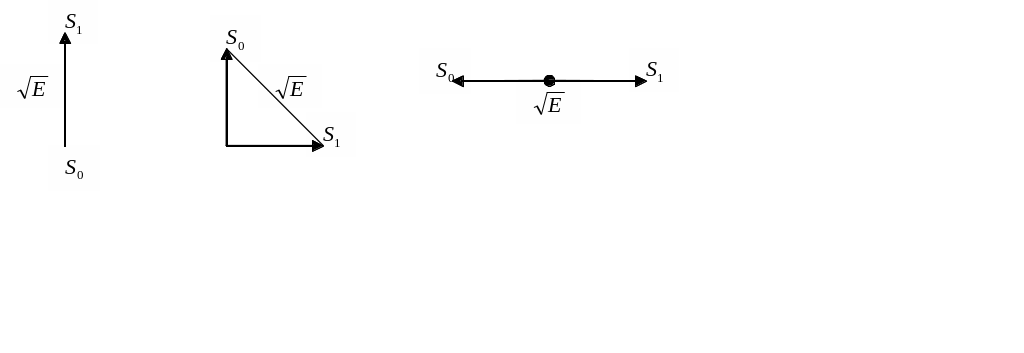
Отже, потенційна перешкодостійкість визначається середньою ймовірністю помилки:

Частотна модуляція з ортогональними сигналами

Два сигналу є радіоімпульси однакової форми з різними несучими частотами, так, що сигнали взаємно ортогональні, рис. б. Енергія різницевого сигналу дорівнює, а середня ймовірність помилки:

Підвищення потенційної завадостійкості при переході від АТ-ПП до частотної телеграфії видається природним, оскільки в другому випадку вдвічі зростає середня потужність передавача. Однак середня імовірність помилки може бути додатково знижена без збільшення потужності передавача, якщо перейти до взаємно зворотним сигналам, рис. в

Фазова модуляція з маніпуляцією фази на 180 °

У 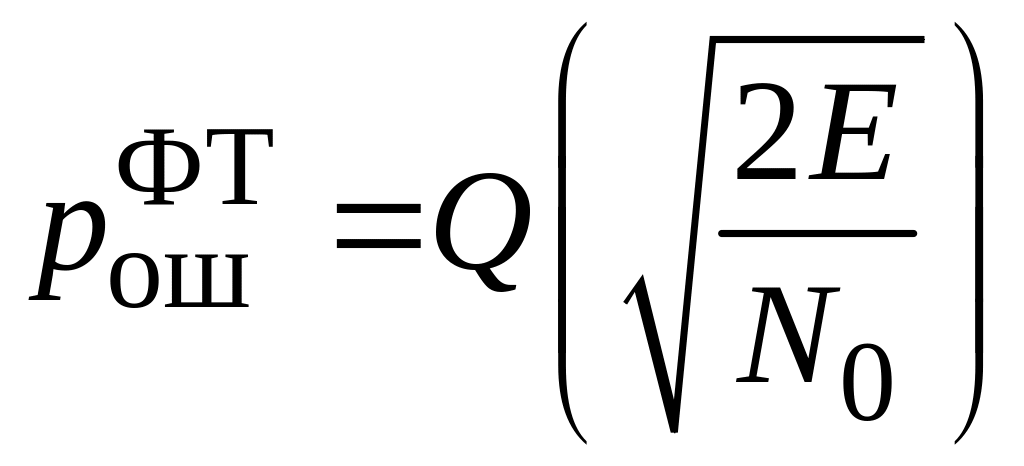разі фазової телеграфії з взаємно зворотними сигналами енергія різницевого сигналу становить . Середня ймовірність помилки дорівнює:

і подальше підвищення потенційної завадостійкості за рахунок вибору форми сигналів при заданій енергії, очевидно, неможливо.

Амплітудна, частотна та фазова модуляція

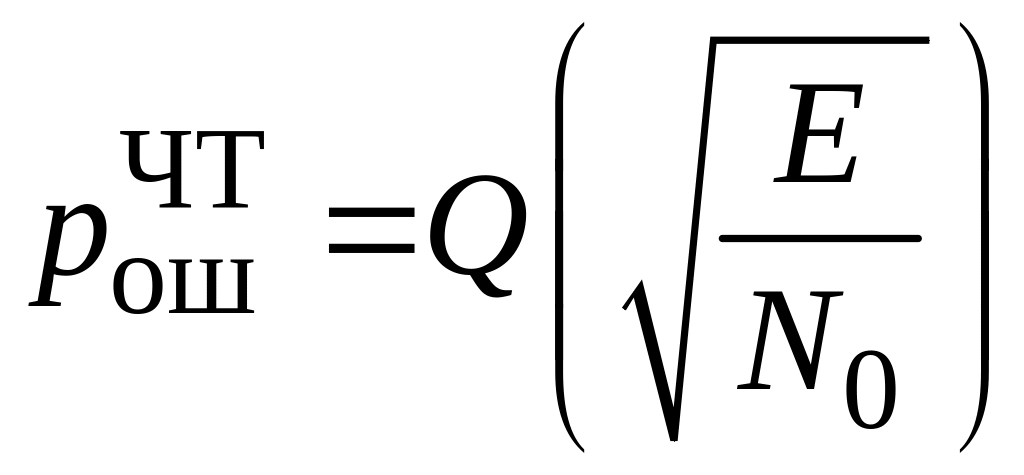
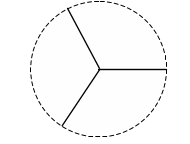
Зауважимо, що якщо використовуються три сигнали однакової енергії, то для досягнення максимальної завадостійкості вони повинні мати взаємний

ф азовий зрушення 120 °, тобто відповідні сигналам точки повинні розташовуватися на колі радіуса в вершинах рівностороннього трикутника:

Я кщо сигналів чотири, то оптимальним є їх розміщення в вершинах правильного тетраедра, вписаного в сферу радіуса . У загальному випадку оптимальний вибір системи із сигналів відповідає їх розташуванню в вершинах правильного -мірного симплекса, вписаного в -мірну сферу: