22. Класифікація сігналів и Завада. Детерміновані та випадкові сигнали.

Фізичний процес одного з параметрів, який міститься в переданому повідомленні, називається сигналом.

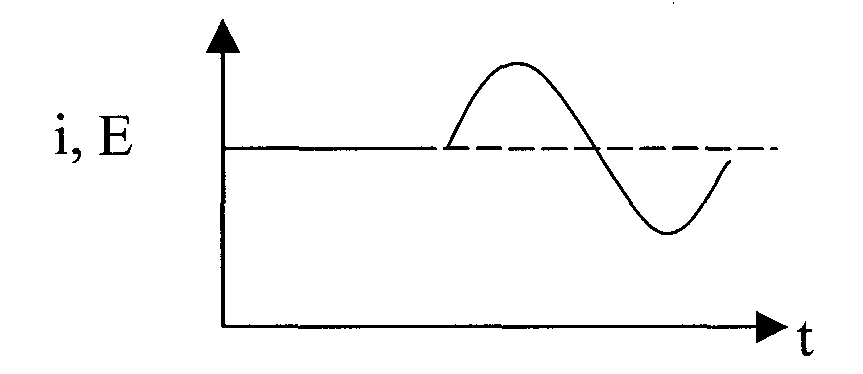
Повідомлення з сигналу можуть бути безперервними і дискретними.

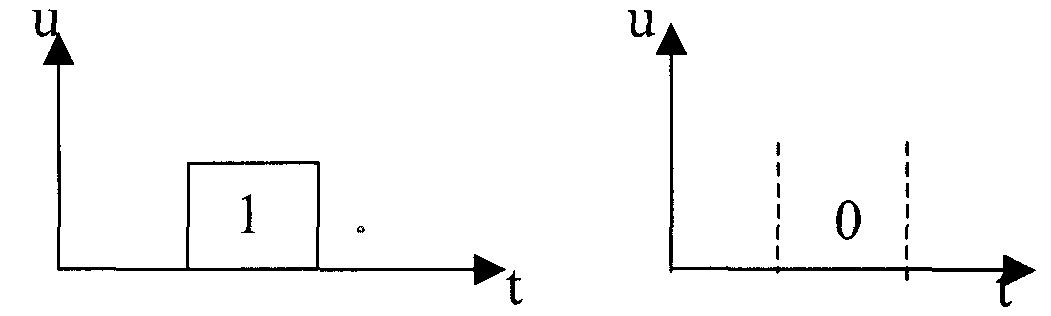
Безперервним називається такий сигнал, який приймає будь-яке значення в заданих межах.

Якщо ж сигнал (або повідомлення) може приймати будь-які значення в деякому інтервалі, то він називається безперервним по станах, або аналоговим.

1) Сигнал, безперервний за рівнем і за часом.

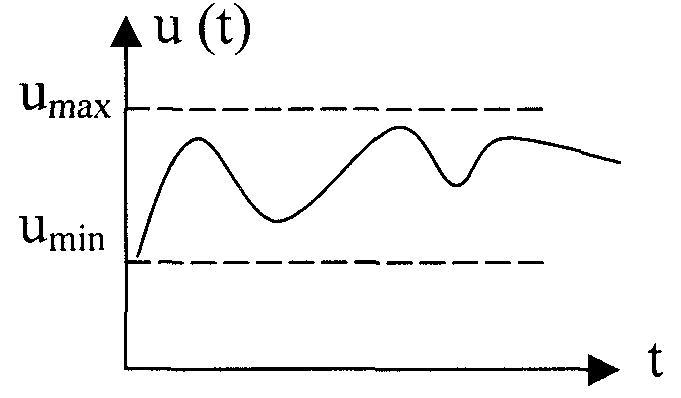
2) Сигнал безперервний - за рівнем і дискретний за часом.

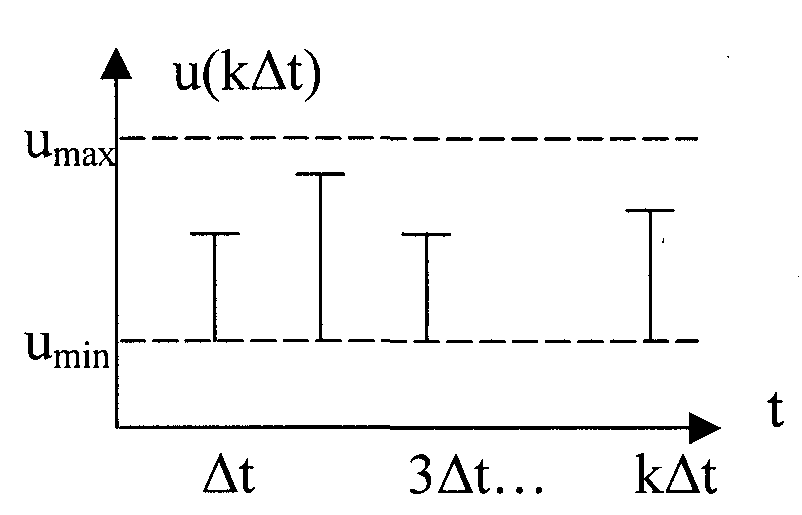
3) Сигнал дискретний за рівнем, безперервний у часі.

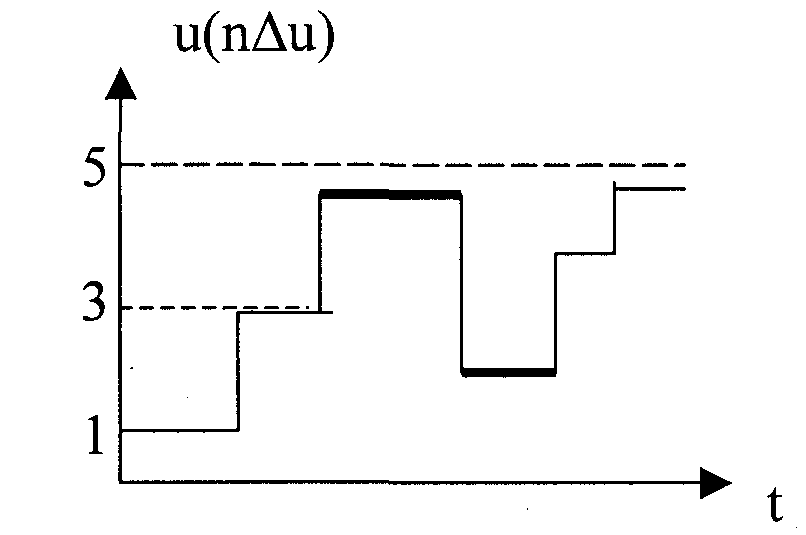
4) Сигнал дискретний за рівнем і за часом.

u(n u)

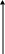
к t

Дискретним за рівнем (3) називається такий сигнал, що приймає тільки певні дискретні значення.

Сигнал дискретний за рівнем іноді називають квантованим сигналом. Сигнал дискретний за рівнем і в часі називається цифровим сигналом (ЦС).

Реальний сигнал є функцією часу і носить випадковий характер. Усі сигнали діляться на:

1. Детерміровані сигнали

2. Випадкові.

Детермінований сигнал - будь-який сигнал, параметри і миттєве значення в момент часу можуть бути передбачені з імовірністю одиниця.

Випадкові сигнали-функції часу, значення заздалегідь невідомі і можуть бути передбачені лише з деякою ймовірністю, меншою одиниці.

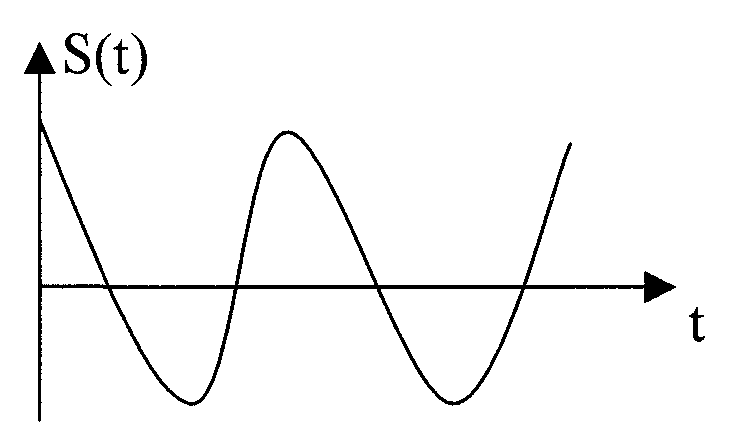
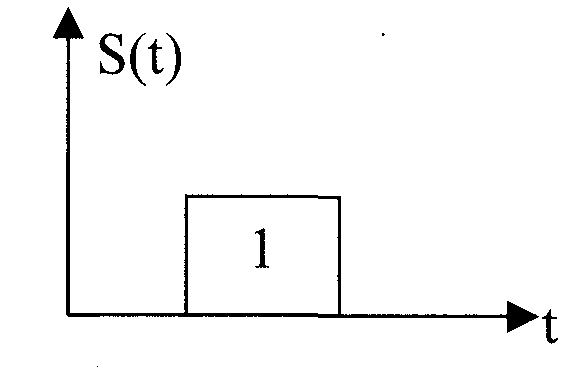
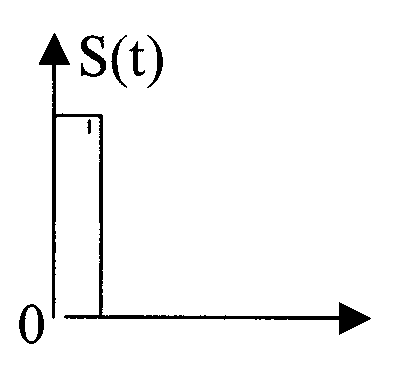
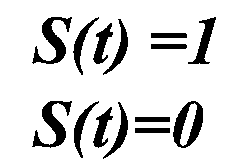
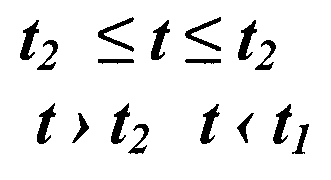
Сигнали відомої форми є випробувальними.

Детерміновані сигнали являють собою відому функцію часу (тобто можна підбирати для них відповідні математичні вирази).

Випадковим називається такий сигнал, миттєве значення якого носить випадковий характер.

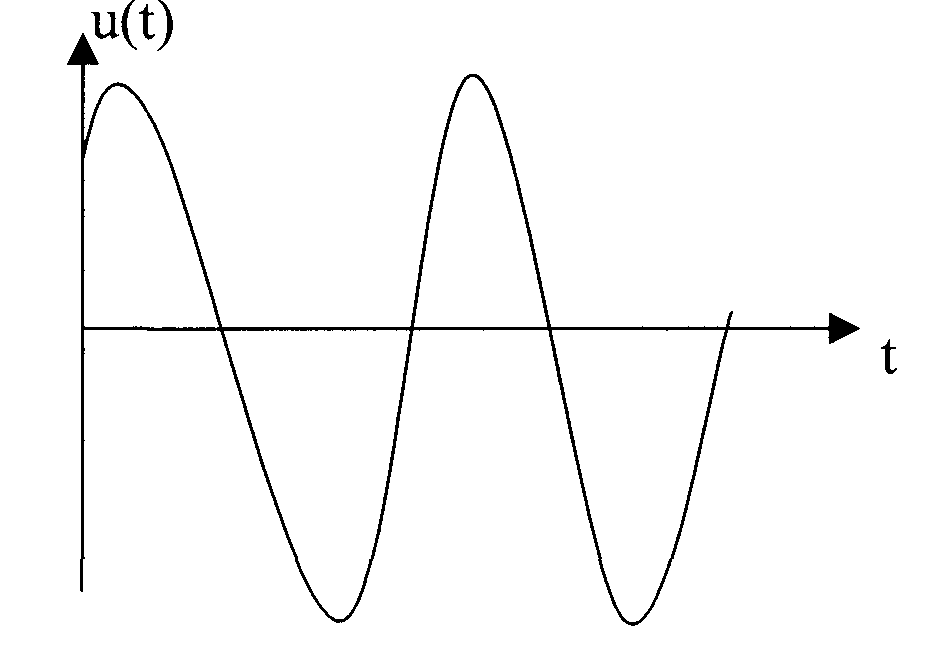
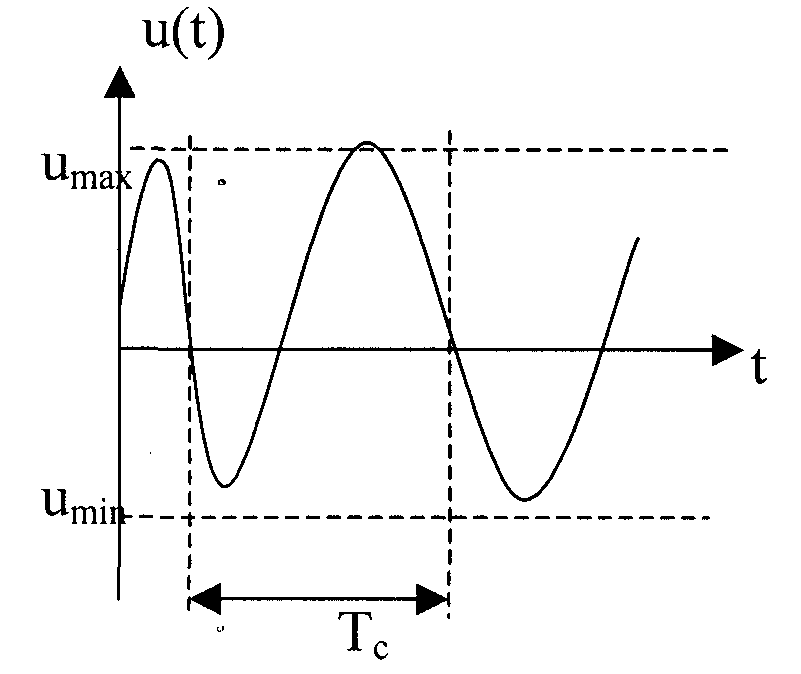
Найбільш повною характеристикою випадкових сигналів (процесів) є їх n-мірний закон розподілу.

Чим більше n тим точніше відомості про поведінку випадкового сигналу (процесу), тобто n -> ∞

При проходженні через КЗ сигнал U (t) спотворюється і U (t) ≠ V (t)

Завадою - називається будь-який вплив на корисний сигнал (або приймач), в результаті якого погіршується достовірність прийнятих сигналів. Перешкоди діляться на зовнішні і внутрішні. До зовнішніх перешкод відносяться: грозові розряди, робота зварювального апарату. електричний транспорт, радіоелектронна медична апаратура. До Внутрішніх перешкод відносяться власні шуми, шуми елементів пристрою. Всі ці перешкоди в залежності від впливу на корисний сигнал S (t), U (t) поділяють на дві групи: 1. Адитивна перешкода - це перешкода яка підсумовується з корисним сигналом S (t) + W (t) = X (t)-адитивна перешкода. 2. Мультиплікативна перешкода X (t) = μ (t) • S (t), де μ (t) - вплив перешкоди на рівень корисного сигналу. Адитивна перешкода може бути флуктуаційної, імпульсної (перешкода, зосереджена в часі), квазігармоніческая (перешкода, зосереджена по частоті).

23. Дискретизація аналогових сигналів. Теорема відліків.

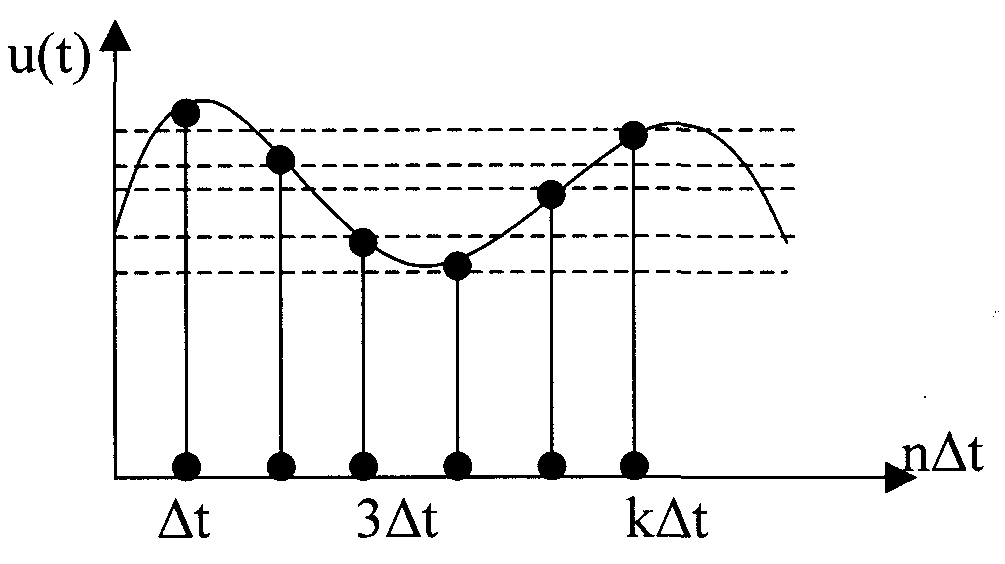
Дискретизація - заміна значень безперервного сигналу U (t) на від-лічильні значення, узяті через проміжки часу Δt = l/2Fe.

Дискретизацією за рівнем називається – квантуванням

В результаті квантування миттєві значення сигналу замінюються значеннями найближчого допустимого або дозволеного рівня сигналу. Відстань між найближчими дозволеними рівнями називається кроком квантування  U. Крок квантування ділиться на: рівномірний; нерівномірний. Цифровий сигнал - сигнал, дискретний в часі і за рівнем (сигнал після дискретизації і квантування).

Перевага дискретизації і квантування - у можливості передавати сигнал дискретним чином. При цьому помилка з'являється тільки в тому випадку, якщо рівень перешкоди перевищує крок квантування. З'являється можливість регенерації сигналів. Інша перевага - можливість передачі по одному каналу.

Теорема відліків Віттакера - Найквіста - Котельникова - Шеннона (теорема Котельникова) свідчіть, Що ЯКЩО безперервній сигнал x (t) має спектр, обмежень частотою Fmax, то ВІН Може буті однозначно и без Втрата відновленій за Своїми дискретними відлікамі, узятімі з частотою f_діскр = 2 * Fmax, або, по-іншому, за відлікамі, узятімі з періодом T_дискр=

Теорему Котельникова можна сформулювати зворотнім чином: Для того, щоб відновити сигнал на прийомі без втрат, необхідно, щоб частота дискретизації була хоча б у два рази більша за максимальну частоту вихідного сигналу. F_д ≥ 2F_max

Теорема Котельникова розглядає ідеальний випадок, коли сигнал почався нескінченно давно й ніколи не закінчиться, а також не має в часовій характеристиці точок розриву. Саме це має на увазі поняття «спектр, обмежений частотою F_max».

Реальні сигнали скінченні у часі і, звичайно, мають у тимчасовій характеристиці розриви, відповідно їх спектр безкінечний. У такому випадку повне відновлення сигналу неможливо й з теореми Котельникова випливають 2 наслідки:

1)Будь-який аналоговий сигнал може бути відновлений з якою завгодно точністю за своїми дискретними відліками, узятими із частотою, де — максимальна частота, якою обмежений спектр реального сигналу.

2)Якщо максимальна частота в сигналі перевищує половину частоти переривання, то способу відновити сигнал з дискретного в аналоговий без перекручувань не існує.