Билет 2
2)Значение физической величины — одно или несколько (в случае тензорной физической величины) чисел, характеризующих эту физическую величину, с указанием единицы измерения, на осн
Производная физическая величина (англ. derived quantity) – физическая величина, входящая в систему
Производными величинами первой очереди являются такие производные величины, в определяющих уравнениях которых присутствуют только основные физические величины. Например, такие производные величины, как скорость и ускорение, явлются производными величинами первой очереди, потому что в их определяющих уравнениях присутствуют только основные величины: длина и время. Производными величинами второй очереди являются производные величины, в определяющих уравнениях которых имеется (кроме основных величин) хотя бы одна величина первой очереди. И так далее в том же порядке. Подобная классификация производных величин необходима, на наш взгляд, при составлении списков (перечней) физических величин в любом справочнике или учебнике, так как только расположение физических величин по признаку их очередности согласуется с принципом причинности. Отметим, что в современных справочниках и учебниках признак очередности в перечнях физических величин не соблюдается. Производные величины когерентны (согласованы), если в их формулах размерности отсутствует числовой коэффициент. В системе единиц СИ все единицы производных величин когерентны. Но этот признак отсутствовал в некоторых системах единиц, существоваших до СИ. Все системы физических величин когерентны, так как размерности их основных величин не зависят друг от друга.величин и определяемая через основные величины этой системы.
3)
Средняя квадратическая погрешность:
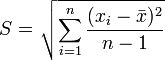
Средняя квадратическая погрешность среднего арифметического:
Средняя квадратичная погрешность 0 ряда измерений А\...АЛ одной и той же величины X равна корню квадратному из среднего арифметического квадратов случайных абсолютных погрешностей этих измерений:[30, С.29] Средняя квадратичная погрешность вычисляется по заданной максимальной допустимой следующим образом:[30, С.31] В теории ошибок доказывается, что средняя квадратичная погрешность линейной функции независимых аргументов равна корню квадратному из суммы квадратов произведений средних квадратичных погрешностей аргументов на коэффициенты при этих аргументах, т. е. средняя квадратичная погрешность среднего арифметического[31, С.43] Коэффициент цср для квадратичной зоны Средняя квадратичная погрешность 'цср = Относительная средняя квадратичная погрешность '0|icp = Результаты тарирования [30, С.233] Примеры: 1. Погрешность измерения подачи насоса. Средняя квадратичная погрешность одиночного измерения подачи сужающим устройством, получающаяся из-за неточности измеренияисходных величин, вычисляется по уравнению (1-53)[30, С.227] Пример 1. Определить погрешность измерения подачи насоса. Средняя квадратичная погрешность одиночного измерения подачи сужающим устройством, получающаяся из-за неточности измерения исходных величин, вычисляются по уравнению (1-61):[31, С.248] Наиболее употребительным критерием оценки точности измерений является средняя квадратичная погрешность о, которая характеризует степень разброса погрешностей и должна подсчитываться по соотношению[31, С.35] При нормальном законе распределения погрешностей можно считать, что абсолютная средняя квадратичная погрешность а связана с максимальной погрешностью Амане соотношением[30, С.29] Для оценки точности измерений возможно применение различных критериев. Наиболее распространенным критерием является средняя квадратичная погрешность.[30, С.29] Графическое осреднение уменьшает погрешности измерения давлений, частоты вращения и величины ун — ^в вдвое. Следовательно, средняя квадратичная погрешность напора в графике характеристики[31, С.250] Если расход определять по диаграмме, записанной самопишущим прибором с помощью планиметра, то для оценки погрешности измерения следует ввести под корень еще два слагаемых: ад и сгпл (<7Д — среднеквадратичная погрешность хода диаграммы и 0пл — среднеквадратичная погрешность планиметрирования).[224, С.73]
Билет 3
2) Методические погрешности определяются несовершенством метода измерения, использованием упрощающих предположений и допущений при выводе расчетных формул, влиянием измерительного прибора на объект измерения. Например, результат измерения температуры с помощью термопары может содержать методическую погрешность, вызванную нарушением температурного режима исследуемого объекта (вследствие внесения термопары).
Инструментальные погрешности зависят от погрешностей применяемых средств измерений. Неточность градуировки, конструктивное несовершенство, изменение характеристик прибора в процессе эксплуатации и другие факторы являются причинами инструментальных погрешностей.
Погрешности измерения возникают также из-за неправильной установки средства измерения, влияния на него магнитных или электрических полей, наличия дополнительных и динамических погрешностей. Дополнительные погрешности обусловлены отклонением условий, в которых работает прибор, от нормальных. Динамические погрешности возникают из-за инерционности применяемых технических средств при достаточно быстрых изменениях измеряемой величины. Все эти погрешности отличают от инструментальных (ГОСТ 8.009-84), поскольку они связаны не столько с самими средствами измерений, сколько с условиями, при которых они работают. Их устранение производится иными способами, нежели устранение инструментальных погрешностей.
Субъективные погрешности определяются неправильным снятием показаний прибора человеком (оператором), что может случиться, например, из-за неправильного направления взгляда при наблюдении за показаниями стрелочного прибора (погрешность от параллакса). Использование цифровых приборов и автоматических методов измерения позволяет исключить такого рода погрешности. Обнаружение причин и источников систематических погрешностей позволяет устранить их или исключить посредством введения поправки.
3)
Коэффицие́нт мо́щности — безразмерная физическая величина, характеризующая потребителя переменного электрического тока с точки зрения наличия в нагрузке реактивной составляющей. Коэффициент мощности показывает, насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Коэффициент мощности необходимо учитывать при проектировании электросетей. Низкий коэффициент мощности ведёт к увеличению доли потерь электроэнергии в электрической сети в общих потерях. Чтобы увеличить коэффициент мощности, используют компенсирующие устройства. Неверно рассчитанный коэффициент мощности может привести к избыточному потреблению электроэнергии и снижению КПДэлектрооборудования, питающегося от данной сети.
Для расчётов в случае гармонических переменных U (напряжение) и I (сила тока) используются следующие математические формулы:
Здесь 
—
активная мощность, 
—
полная мощность, 
—
реактивная мощность.
Билет 4
1)
Абсолютная погрешность – это значение, вычисляемое как разность между значением величины, полученным в процессе измерений, и настоящим (действительным) значением данной величины.
Абсолютная погрешность меры – это значение, вычисляемое как разность между числом, являющимся номинальным значением меры, и настоящим (действительным) значением воспроизводимой мерой величины.
Относительная погрешность – это число, отражающее степень точности измерения.
Приведенная погрешность – это значение, вычисляемое как отношение значения абсолютной погрешности к нормирующему значению.
Инструментальная погрешность – это погрешность, возникающая из-за допущенных в процессе изготовления функциональных частей средств измерения ошибок.
Методическая погрешность – это погрешность, возникающая по следующим причинам:
неточность построения модели физического процесса, на котором базируется средство измерения;
неверное применение средств измерений.
Субъективная погрешность – это погрешность возникающая из-за низкой степени квалификации оператора средства измерений, а также из-за погрешности зрительных органов человека, т. е. причиной возникновения субъективной погрешности является человеческий фактор.
Статическая погрешность – это погрешность, которая возникает в процессе измерения постоянной (не изменяющейся во времени) величины.
Динамическая погрешность – это погрешность, численное значение которой вычисляется как разность между погрешностью, возникающей при измерении непостоянной (переменной во времени) величины, и статической погрешностью (погрешностью значения измеряемой величины в определенный момент времени).
Аддитивная погрешность – это погрешность, возникающая по причине суммирования численных значений и не зависящая от значения измеряемой величины, взятого по модулю (абсолютного).
Мультипликативная погрешность – это погрешность, изменяющаяся вместе с изменением значений величины, подвергающейся измерениям.
Систематическая погрешность – это составная часть всей погрешности результата измерения, не изменяющаяся или изменяющаяся закономерно при многократных измерениях одной и той же величины.
Случайная погрешность – это составная часть погрешности результата измерения, изменяющаяся случайно, незакономерно при проведении повторных измерений одной и той же величины.
2)