3.3.4 Загальний вигляд задачі оптимального управління

Незважаючи на велике різноманіття задач оптимального управління, всі вони можуть бути представлені в одному узагальненому вигляді. Всі задачі управління характеризуються цілеспрямованістю, тобто направлені на отримання певного результату. Цей результат може бути різним: наприклад, отримання максимального прибутку, мінімізації витрат, економії ресурсів тощо. Све це різноманіття кінцевих результатів математично виражається цільовою функцією (ЦФ):

ЦФ1 : П_{рибуток} → max ( прибуток повинен бути направлений до максимуму)

ЦФ2 : В_{артість} → min ( вартість проекту повинна бути мінімізована)

ЦФ3 : В_итрати→ min (витрати на реалізацію роботи повинні бути мінімальними)

Зрозуміло, що залежно від обраного методу рішення задачі, математичний вираз цільової функції може бути різним.

Іншою важливою частиною будь-якої задачі управління є формалізований опис умов, в яких вона повинна вирішуватися. Як правило, ці умови мають обмежувальний характер. Наприклад, на будь-якому підприємстві майже завжди спостерігається нестача фінансових ресурсів, енергетичних і т.д. Подібні обмеження також мають певний математичний вираз:

ОБМ 1 : Ф ≤ в₁ (фінансові витрати не повинні перевищувати величину в₁ )

ОБМ 2 : Е ≥ в₂ ( енергетичні витрати не повинні перевищувати величину в₂ )

В кожній задачі управління фігурують і змінні. Наприклад, кількість продукції різного виду, які випускає підприємство: Х₁, Х₂, Х_і. Для підприємств зв'язку частіше використовують термін "послуги", який по значенню прирівнюється до терміну "продукція". Ці змінні завжди мають позитивне значення, що визначається граничними умовами:

ГРУ : Х_і > 0

Таким чином, будь-яка задача управління може бути представлена у вигляді трьох складових: цільової функції, обмежень і граничних умов. Загальний вид задачі оптимального управління такий:

ЦФ : П → max (min);

З₁ ≤ а₁

Обмеження З₂ ≤ а₂

З_і ≤ а_і

Г раничні ∞ > х₁ ≥ 0;

умови

∞ > х₂ ≥ 0;

∞ > х_j ≥ 0.

Конкретизація задачі оптимального управління буде проведена на прикладі лінійного програмування.

3.4 Метод лінійного програмування як приклад вирішення проблем оптимізації управління [19, 27]

Метод лінійного програмування є самим розробленим і часто застосовується. Задачі лінійного програмування є формалізованими, є відпрацьований математичний апарат і необхідне програмне забезпечення для її рішення на ЕОМ. Далі розглянемо загальну форму задачі лінійного програмування, методи її рішення і конкретний приклад задачі стосовно до роботи підприємств зв'язку.

3.4.1 Загальна форма задачі лінійного програмування та її складові

В загальному вигляді задача лінійного програмування має такий вигляд: необхідно знайти максимум (мінімум) цільової функції

С = ∑ с_j * x_j → min (max)

П ри обмеженнях ∑а_{і j} х _j ≤ в_j ; i=1,m; j=1,r; ∞ > х_j ≥ 0.

В розгорнутому вигляді задача може бути представлена наступним чином:

ЦФ:С = с₁х₁+с₂х₂+...+с_j х _j+...+с _rх _r→ min(max)

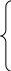а₁₁ х₁ +а₁₂х₂+...+ а_{1 j} х _j+...+ а_{1 r}х _r ≤ в₁

а₂₁ х₁+а₂₂х₂+...+а_{2 j} х _j+...+ а_{2 r}х _r ≤ в₂

ОБМ а_і1 х₁+а_і2х₂+...+а_{і j} х _j+...+ а_{і r}х _r ≤ в_і

а_m1 х1+а_m2х₂+...+а_{m j} х _j+...+ а_{m r}х _r ≤ в_m

ГРУ : ∞ > х_j ≥ 0.

Таким чином, всі вирази, які входять в склад задачі лінійного програмування, представляють лінійні залежності змінних між собою.