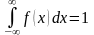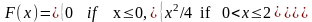1-37
For opposite events
and
one of the following equalities holds:
The probability of an arbitrary event cannot be:
< 0
Two events form a complete group if they are:
Opposite
How many 5-place telephone numbers are there if the digit “0” is not used on the first place?
90000
There are 6 identical balls numbered by 1, 2..., 6 in a box. All balls by one are randomly extracted from the box. Find the probability that the numbers of extracted balls will appear in ascending (increasing) order.
1/720
The events A and B are independent, Р(А) = 0,3; Р(В) = 0,1. Find
.
0,07
Two independent events A and B are compatible,
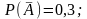and
Find
.
0,97
If an event A can happen only provided that one of incompatible events В1, В2, В3 forming a complete group will occur, Р(А) is calculated by the following formula:
If an event A can happen only provided that one of incompatible events В1, В2, В3, В4 forming a complete group will occur, РА(В2) is calculated by the following formula:
It is known that 10% of all radio lamps are non-standard. Find the probability that there will be no more than 1 non-standard lamp among 4 randomly taken radio lamps.
We say that a discrete random variable X is distributed under a binomial law if
We say that a discrete random variable X is distributed under Poisson law with parameter if
We say that a discrete random variable X is distributed under a geometrical law if
There is no true answer
A random variable X is distributed under Poisson law with parameter . Find M(X).
M (X) =
A random variable X is distributed under a binomial law. Find M(X).
M (X) = np
Dispersion of a discrete random variable X is
Dispersion of a constant C is
0
An improper integral of density of distribution in limits from – till is equal to
A random variable X is given by density of distribution of probabilities:
Find
the function of distribution F(x).
5 independent trials are made, and in each of them an event A occurs with probability р. The probability that the event A will occur at least once is:
The mathematical expectation of a continuous random variable X of which possible values belong to an interval [a, b] is
The dispersion D(X) of a continuous random variable X is determined by the following equality:
A distribution of probabilities of a continuous random variable X is exponential if it is described by the density
A random variable X is normally distributed with parameters a and 2 if its density f(x) is:
The function of distribution of an exponential law has the following form:
The mathematical expectation of a random variable X uniformly distributed in an interval (0, 1) is equal to
½
The probability that a continuous random variable X will take on a value belonging to an interval (a, b) is equal to
Show the differential function of a uniformly distributed random variable:
Four events form a complete group if they are:
there is no correct answer
It is known that 20 % of all details are non-standard. 6 details have been randomly taken. Find the probability that there is no more than 1 non-standard detail of the taken.
A random variable X is given by the density of distribution of probabilities:
Find the function of distribution F(x).
Events A1, A2, A3, A4 are called independent in union if:
Each two of them are independent and each event and all possible products of the rest events are independent.
If X is uniformly distributed over (0, 10), calculate the probability that X < 3:
0,3
If X is uniformly distributed over (0, 10), calculate the probability that X > 6:
0,4
A random variable X is distributed under an exponential law with parameter = 0,5. Find the mathematical expectation of X:
2
A random variable X is distributed under an exponential law with parameter = 0,5. Find the dispersion of X:
4
A die is tossed before the first landing 6 aces. Find the probability that the first appearance of 6 will occur at the third tossing the die.
25/216
1. A reliable event is: an event that necessarily will happen if a certain set of conditions S holds.
2. The probability of a reliable event is the number: 1
3. An impossible event is: event that certainly will not happen if the set of conditions S holds.
4. The probability of impossible event is the number: 0
5. A random event is: an event that can either take place, or not to take place for holding the set of conditions S.
6. The probability of a random event A is the number: 0<p<1
7.
Probabilities of opposite events A and
satisfy the following condition: P(A)+P(
)=1;
P(A)-P(
)=Ø;
P(A)*P(
)=0
8. Let A and B be opposite events. Find Р(В) if Р(А) = 1/6. 5/6
9. If pairwise incompatible events form a complete group, the sum of their probabilities is equal to: 1
10. Let A and B be events connected with the same trial. Show the event that means simultaneous occurrence of A and В. P=AB
11. Let A and B be events connected with the same trial. Show the event that means occurrence of only one of events A and B.
A*B s 4ertoi + *B
112. Let А1, А2, А3 be events connected with the same trial. Let A be the event that means occurrence only one of events А1, А2 and А3. Express the event A by the events А1, А2 and А3. 1* 2*A3 + 1*A2* 3+A1* 2* 3
113. Let А1, А2, А3 be events connected with the same trial. Let A be the event that means none of events А1, А2 and А3 have happened. Express the event A by the events А1, А2 and А3 vse A s 4ertami
114. Let n be the number of all outcomes, m be the number of the outcomes favorable to the event A. The classical formula of probability of the event A has the following form: P(A) = m/n
115. The probability of an arbitrary event cannot be: less than 0, more than 1
116. The dispersion D(X) of a random variable X is equal to 2,25. Find (Х): 15
117. A coin is tossed twice. Find the probability that "heads" will land in both times. 1/4
118. A coin is tossed twice. Find the probability that "heads" will land at least once. 1-1/4=3/4
119. There are 1000 tickets in a lottery. 500 of them are winning, and the rest 500 are non-winning. Two tickets have been bought. What is the probability that both tickets are winning? 0,2498
120. Two dice are tossed. Find the probability that the sum of aces does not exceed 3. 1/12
121. Two dice are tossed. Find the probability that the sum of aces doesn’t exceed 4. 1/6
122. Two dice are tossed. Find the probability that the product of aces does not exceed 2. 1/12
123. There are 10 white, 15 black, 20 blue and 25 red balls in an urn. One ball is randomly extracted from the urn. Find the probability that the extracted ball is white or black. 5/14
124. There are 9 white and 1 black balls in an urn. Three balls are randomly extracted from the urn. What is the probability that all balls are white? 7/10
125.
Calculate
:
455
126.
Calculate
:
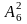30
127. One letter is randomly chosen from the word "COMEDY". What is the probability that this letter is "U"? 0
128. The letters T, A, O, M have been written on four cards. The cards are shuffled and randomly put in a row. What is the probability that the word "ATOM" will be in the row? 1/24
129. There are 4 white and 3 black balls in an urn. Two balls are randomly extracted from the urn. What is the probability that both balls are white? 2/7
130. There are 12 white, 10 black, 10 yellow and 20 red balls in a box. Find the probability that a randomly taken ball is white. 3/13
131. There are 10 white, 15 black, 10 yellow and 25 red balls in a box. Find the probability that a randomly taken ball is black. 1/4
132. How many 5-place telephone numbers are there if the digit “0” is not used on the first place? 90000
133. Two dice are tossed. What is the probability that the sum of aces will be more than 10? 1/12
134. A coin is tossed 8 times. Find the probability that “heads” will land 6 times. 7/64
135. There are 5 children in a family. Assuming that probabilities of birth of boy and girl are equal, find the probability that the family has three boys: 5/16
136. Two shots are made in a target by two shooters. The probability of hit by the first shooter is equal to 0,8, by the second - 0,9. Find the probability of at least one hit in the target. 0,98
137. There are 4 books on mathematics and 6 books on chemistry on a book shelf. Three books are randomly taken from the shelf. Find the probability that all taken 3 books are on mathematics. 1/30
138. There are 4 standard and 3 non-standard details in a box. Two details are randomly taken from the box. Find the probability that only one detail is standard. 4/7
139. Three shooters shoot in a target. Probability of hit in the target by the 1st shooter is 0,75; by the 2nd - 0,8 and by the 3rd - 0,9. Find the probability of hit by all the shooters. 0,54
140. A student knows 8 of 11 questions of an exam. Find the probability that he knows 3 randomly chosen questions. 56/165
141. A die is tossed. Find the probability that an even number of aces will land. 1/2
142. Two shooters shoot in a target. The probability of hit by the 1st shooter is 0,6, and by the 2nd - 0,7. Find the probability that at least one of shooters will hit in the target. 0,88
143. Two shooters shoot in a target. The probability of hit by the first shooter is 0,6, and by the second - 0,7. Find the probability that only one of shooters will hit in the target. 0,46
144. Three dice are tossed. Find the probability that the sum of aces will be 5. 1/36
145. If A and B are independent events then for Р(АВ) one of the following equalities holds: P(A)*P(B)
146. There are 4 white and 6 black balls in an urn. Two balls are randomly taken from the urn.
What is the probability that both balls are black? 1/3
147. There are 15 details in a box, and 10 of them are painted. Three details are randomly extracted from the box. Find the probability that the extracted details are painted. 24/91
148. There are 3 defective lamps among 10 electric lamps. Find the probability that two randomly chosen lamps will be defective. 1/15
149. Probability to fail exam for the first student is 0,3; for the second – 0,5; and for the third – 0,1. What is the probability that only one of them will pass the exam? 0,185
150. The probability of delay for the train №1 is equal to 0,2, and for the train №2 - 0,64. Find the probability that at least one train will be late. 0,872
151. The probability of delay for the train №1 is equal to 0,2, and for the train №2 - 0,64. Find the probability that both trains will be late. 0,128
152. If the probability of a random event A is equal to P(A), the probability of the opposite event is equal to: 1-P( )
153.
Show the formula of total probability:
154. Function of distribution of a random variable X is given by the formula
.
Find density of distribution f(x). proizvodnuyu naiti 2cos2x
155. If an event A can happen only provided that one of pairwise incompatible events В1, В2, В3 forming a complete group will occur, Р(А) is calculated by the following formula: kak v 153 voprose
156. Electric lamps are made at two factories, and the first of them delivers 70%, and the second - 30% of all consumed production. 83 of each hundred lamps of the first factory are standard on the average, and 63 - of the second factory. Find the probability that a bought lamp will be standard. 0,77
157. The probability of hit in 10 aces for a shooter at one shot is 0,8. Find the probability that for 10 independent shots the shooter will hit in 10 aces exactly 7 times. 0,201
158. There are 5 children in a family. Assuming that probabilities of birth of boy and girl are equal, find the probability that there are 3 girls and 2 boys in the family.