
- •Расчет подъемного крана
- •Cиловой расчет параметров процесса резания
- •Нагревание тела из неоднородного материала
- •Функции многих переменных
- •Решение
- •4.2 Предел и непрерывность функции двух переменных
- •4.3 Частные производные
- •Геометрическая интерпретация частных производных
- •Варианты к заданию.
- •Частные производные второго порядка
- •Производная сложной функции
- •Примеры вычисления производных
- •Неявная функция и ее производная
Производная сложной функции
1. Пусть z=f(x,y), x=x(t), y=y(t). Тогда z=f(x(t), y(t)) является сложной функцией одного переменного t, и ее производная по t может быть вычислена по формуле:
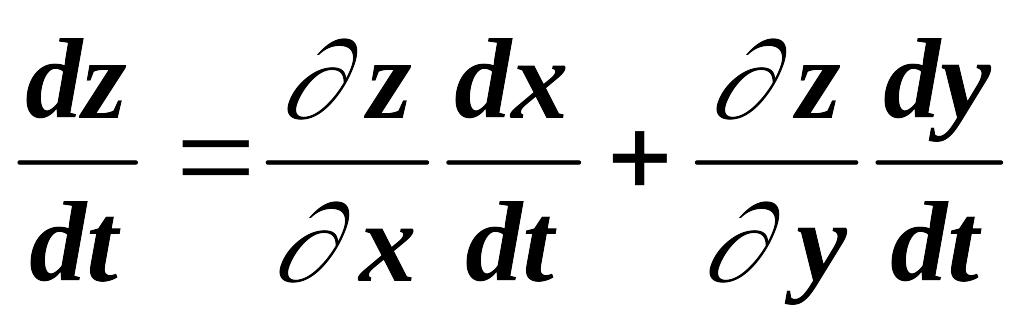 .
.
2. Пусть z=f(x,y), x=x(u, v), y=y(u, v). Тогда z = f(x(u,v), y(u, v)) является сложной функцией двух переменных u и v, и ее частные производные можно вычислить по формулам:
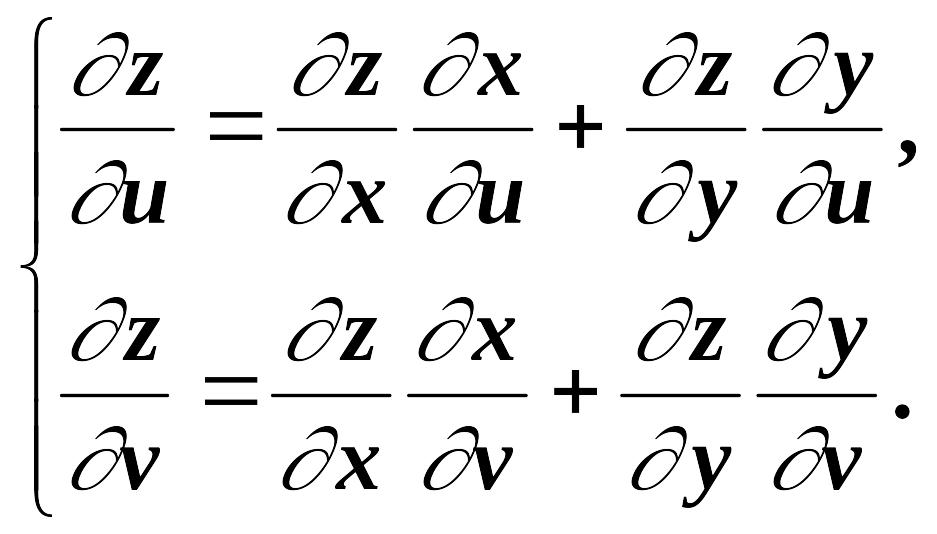
Примеры вычисления производных
Пример 1.
Найти
производную
![]() ,
если
,
если
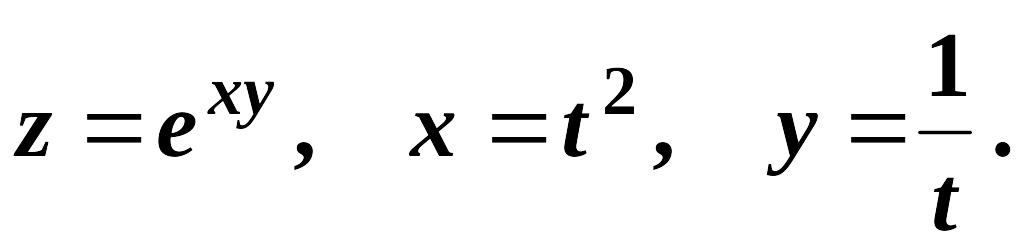
Решение: Применим формулу .
![]() =
=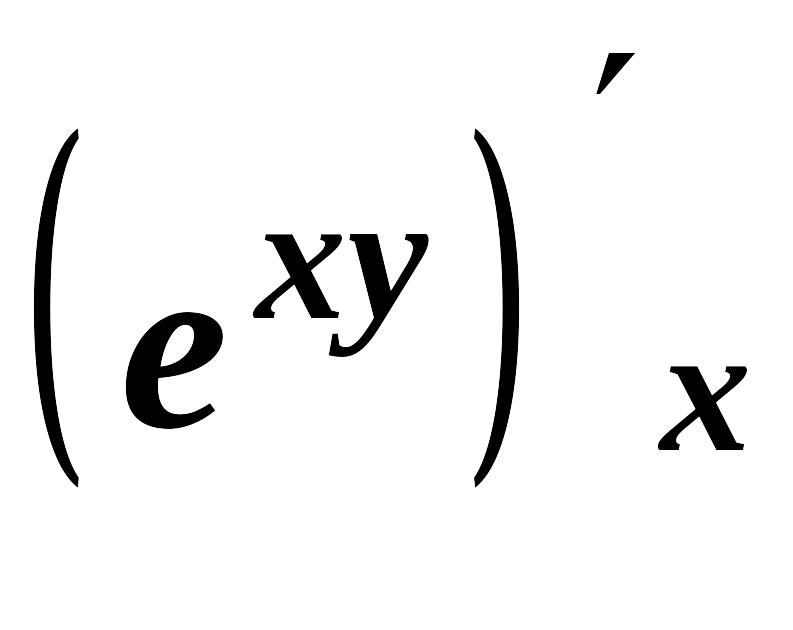 =
=![]() y;
y;
![]() =
=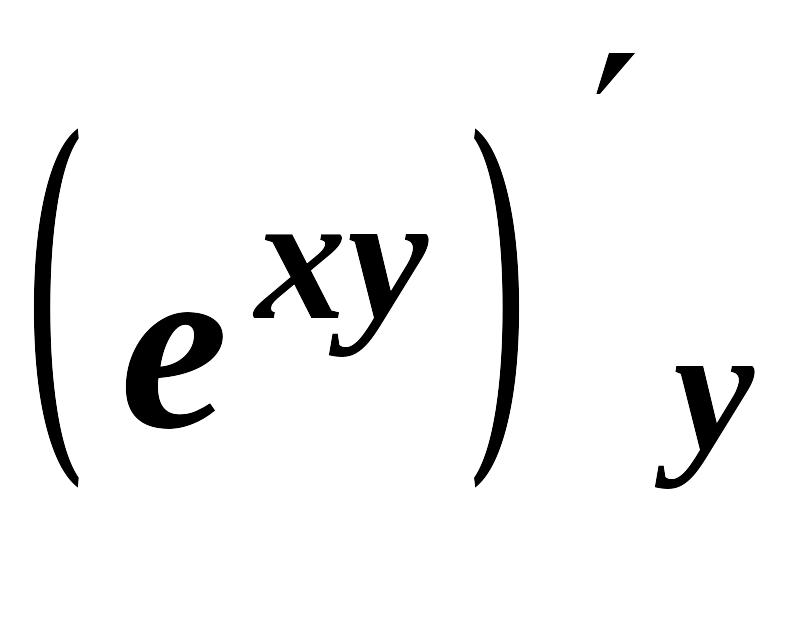 =
×
x;
=
×
x;
![]() =2t;
=2t;
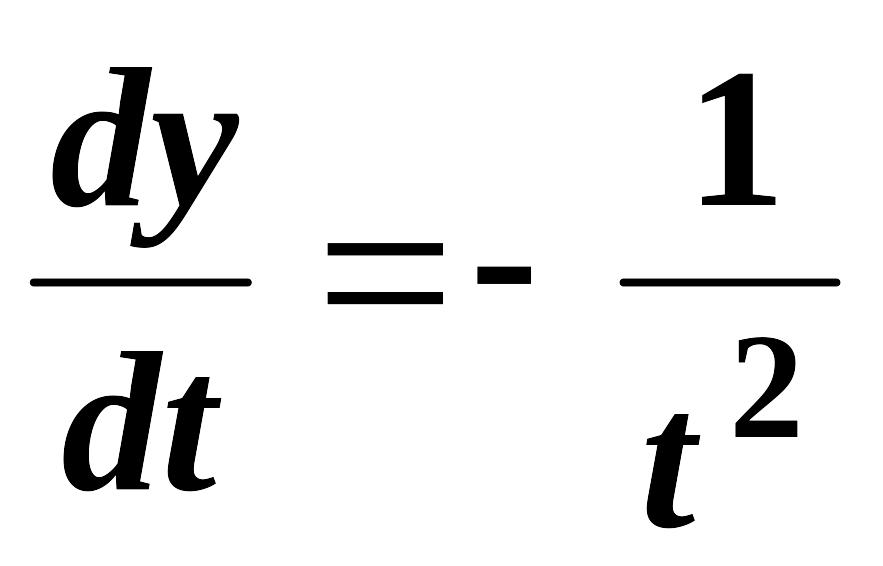 ;
;
![]() =
×y×2t
+
×
x×
=
×y×2t
+
×
x×![]() .
.
Выразив x и y через t, получим
=![]() (2–1)=
.
Ответ:
=
.
(2–1)=
.
Ответ:
=
.
В данном примере
проще было сначала выразить z
через t,
а затем найти
:
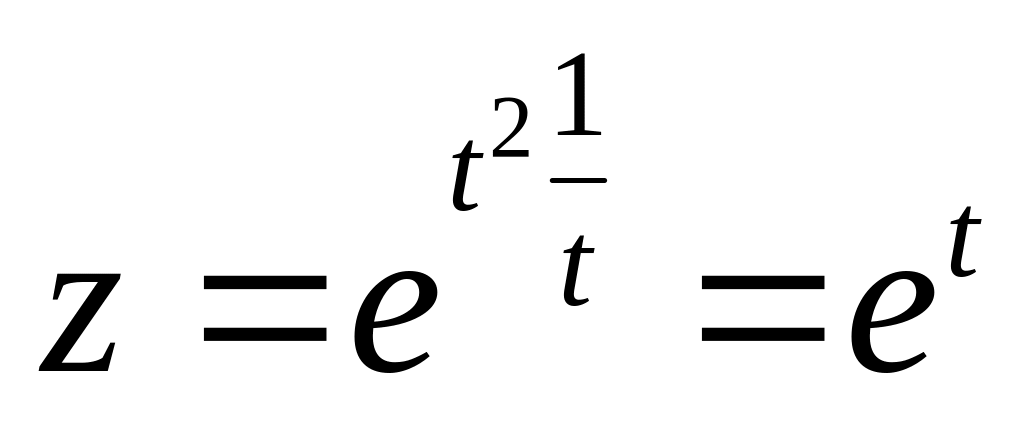 ,
,
 .
Данную формулу следует использовать,
если функция
.
Данную формулу следует использовать,
если функция
![]() неудобна
для дифференцирования.
неудобна
для дифференцирования.
Пример 2.
Найти
производную
![]() если z=x2+y2,
если z=x2+y2,
y=
![]() .
.
Решение.
Применим формулу
,
здесь t
= x,
и формула примет вид:
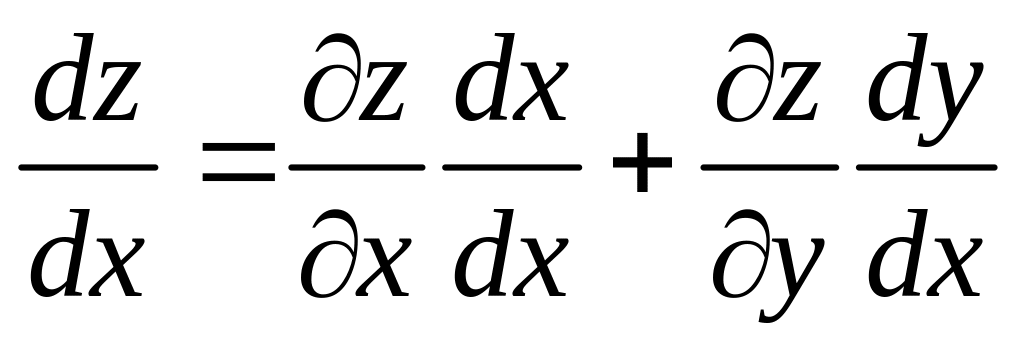 .
.
=2x;
=2y;
![]() =1;
=1;
![]() =
–
=
–![]() ;
;
Ответ:
=2х
– 2y
=2х
– 2
=![]()
Если выразим z через х и продифференцируем по х, получим тотже ответ:
![]() ,
,

Пример 3.
Найти
производные
![]() и
и
![]() , если z=xy2,
x=u2,
y= ln
v.
, если z=xy2,
x=u2,
y= ln
v.
Решение.
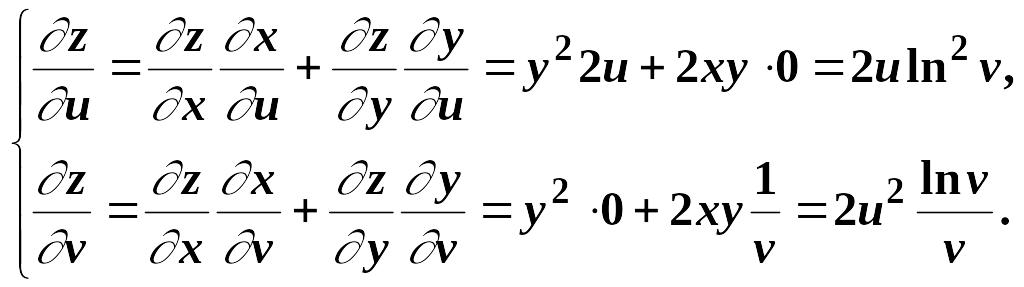
Задание.
Найти
|
||
1.
|
2.
|
3.
|
4.
|
5.
|
6.
|
Найти
|
||
1. |
2. |
3.
|
4.
|
5.
|
6.
|
Найти
|
||
1. |
2. |
3.
|
4.
|
5.
|
6.
|
Неявная функция и ее производная
Определение. Пусть функция z=F(x,y) определена и непрерывна в некоторой области. Пусть существует непрерывная функция y=f(x) такая, что пары (x,y) удовлетворяют уравнению
F(x,y)=0.
В этом случае данное уравнение задает неявно функцию y=f(x).
Замечание.
В действительности может не существовать
ни одной функции
y=f(x),
удовлетворяющей уравнению F(x,y)=0,
или может
существовать несколько таких функций.
Например, не существует функции
y=f(x),
удовлетворяющей уравнению x2+y2+1=0,
а
для уравнения
x2+y2–1=0
существует
две функции, которые ему удовлетворяют:
![]() и
и
![]() .
.
Пример. Функция y=f(x) задана неявно уравнением: xy+x+y–1=0. Найти эту функцию в явном виде.
Искомую функцию найдем, разрешив уравнение относительно y:
y=(1–x)/(1+x).
Можно вычислять производные от функции y=f(x), заданной неявно, через частные производные функции F(x,y)= xy+x+y–1. Для этого приведем без доказательства следующую теорему.
Теорема. Если непрерывная функция y=f(x) задана в неявном виде уравнением F(x,y)=0, и если частные производные Fx¢ (x,y) и Fy¢(x,y) непрерывны, то функция y=f(x) имеет производную для каждого значения x, для которого
F¢y(x,y)¹ 0 и эта производная выражается формулой
![]() .
.
Пример. Найти производную функции y=f(x), заданной неявно уравнением: xy+x+y–1=0.
Решение.
F(x,y)=
xy+x+y–1,
![]() ,
,
![]() .
.
Поэтому
![]() =
–
=
–
![]() .
Так как y=(1–x)/(1+x),
то
.
Так как y=(1–x)/(1+x),
то
=
–![]() .
.
Такой же результат получим, взяв производную от функции, записанной в явном виде:
=![]() .
.
